We collect evidence in support of a conjecture of Griffiths, Green, and Kerr on the arithmetic of extension classes of limiting mixed Hodge structures arising from semistable degenerations over a number field. After briefly summarizing how a result of Iritani implies this conjecture for a collection of hypergeometric Calabi–Yau threefold examples studied by Doran and Morgan, the authors investigate a sequence of (non-hypergeometric) examples in dimensions 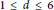$1\,\le \,d\,\le \,6$ arising from Katz's theory of the middle convolution. 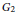A crucial role is played by the Mumford-Tate group (which is ${{G}_{2}}$ ) of the family of 6-folds, and the theory of boundary components of Mumford–Tate domains.