The problem of the best fit to set ideal values under general inequality order restrictions is examined for asymmetric, quadratic, absolute, and Chebyshev norms. Special solution procedures are given in terms of network flow algorithms over a network associated with the given isotonic order relations, and the nature of the optimal solutions is characterized for the different norms.
The model is formulated in terms of finding an optimal insurance rate structure over given risk classes for which a desired pattern of tariffs can be specified. The suitability of different norms is considered in the context of corporate profitability, and the relationship to a simple rate relativities model is described.

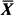 is a minimax estimator in the class of all measurable estimators and all possible distributions. This effort extends some earlier work of Bühlmann to a more general setting.
is a minimax estimator in the class of all measurable estimators and all possible distributions. This effort extends some earlier work of Bühlmann to a more general setting.