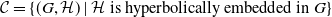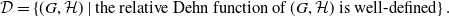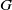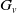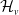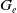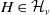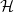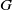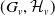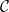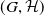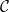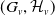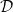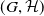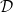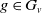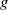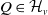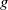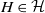Consider the following classes of pairs consisting of a group and a finite collection of subgroups:

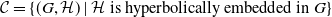• • $ \mathcal{C}= \left \{ (G,\mathcal{H}) \mid \text{$\mathcal{H}$ is hyperbolically embedded in $G$} \right \}$

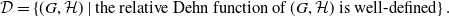• • $ \mathcal{D}= \left \{ (G,\mathcal{H}) \mid \text{the relative Dehn function of $(G,\mathcal{H})$ is well-defined} \right \} .$

Let 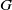$G$ be a group that splits as a finite graph of groups such that each vertex group 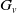$G_v$ is assigned a finite collection of subgroups 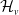$\mathcal{H}_v$, and each edge group 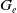$G_e$ is conjugate to a subgroup of some 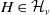$H\in \mathcal{H}_v$ if $e$ is adjacent to $v$. Then there is a finite collection of subgroups 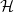$\mathcal{H}$ of 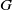$G$ such that

1. 1. If each 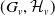$(G_v, \mathcal{H}_v)$ is in 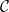$\mathcal C$, then 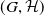$(G,\mathcal{H})$ is in 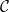$\mathcal C$.

2. 2. If each 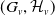$(G_v, \mathcal{H}_v)$ is in 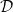$\mathcal D$, then 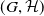$(G,\mathcal{H})$ is in 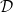$\mathcal D$.

3. 3. For any vertex $v$ and for any 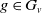$g\in G_v$, the element 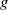$g$ is conjugate to an element in some 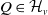$Q\in \mathcal{H}_v$ if and only if 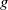$g$ is conjugate to an element in some 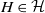$H\in \mathcal{H}$.

That edge groups are not assumed to be finitely generated and that they do not necessarily belong to a peripheral collection of subgroups of an adjacent vertex are the main differences between this work and previous results in the literature. The method of proof provides lower and upper bounds of the relative Dehn functions in terms of the relative Dehn functions of the vertex groups. These bounds generalize and improve analogous results in the literature.

We give technical conditions for a quasi-isometry of pairs to preserve a subgroup being hyperbolically embedded. We consider applications to the quasi-isometry and commensurability invariance of acylindrical hyperbolicity of finitely generated groups.