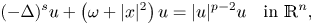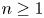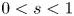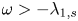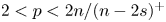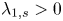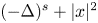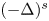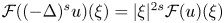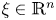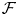1 results
Uniqueness of ground states to fractional nonlinear elliptic equations with harmonic potential
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-14
-
- Article
-
- You have access
- HTML
- Export citation
-
In this paper, we prove the uniqueness of ground states to the following fractional nonlinear elliptic equation with harmonic potential,
\[ (-\Delta)^s u+ \left(\omega+|x|^2\right) u=|u|^{p-2}u \quad \mbox{in}\ \mathbb{R}^n, \]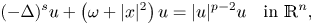where $n \geq 1$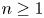
, $0< s<1$
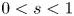, $\omega >-\lambda _{1,s}$
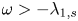, $2< p< {2n}/{(n-2s)^+}$
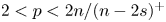, $\lambda _{1,s}>0$
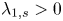is the lowest eigenvalue of $(-\Delta )^s + |x|^2$
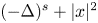. The fractional Laplacian $(-\Delta )^s$
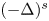is characterized as $\mathcal {F}((-\Delta )^{s}u)(\xi )=|\xi |^{2s} \mathcal {F}(u)(\xi )$
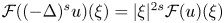for $\xi \in \mathbb {R}^n$
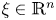, where $\mathcal {F}$
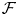denotes the Fourier transform. This solves an open question in [M. Stanislavova and A. G. Stefanov. J. Evol. Equ. 21 (2021), 671–697.] concerning the uniqueness of ground states.
