1 results
Annihilators and Power Values of Generalized Skew Derivations on Lie Ideals
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 2 / 01 June 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 258-270
- Print publication:
- 01 June 2016
-
- Article
-
- You have access
- Export citation
-
Let
$R$ be a prime ring of characteristic diòerent from 
$2$, let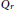 
${{Q}_{r}}$ be its right Martindale quotient ring, and let 
$C$ be its extended centroid. Suppose that 
$F$ is a generalized skew derivation of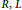 
$R,\,L$ a non-central Lie ideal of 
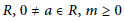$R,\,0\,\ne \,a\,\in \,R,\,m\,\ge \,0$ and 
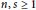$n,\,s\,\ge \,1$ fixed integers. If
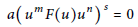$$a{{\left( {{u}^{m}}F\left( u \right){{u}^{n}} \right)}^{s}}\,=\,0$$for all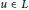
$u\,\in \,L$, then either 
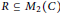$R\,\subseteq \,{{M}_{2}}\left( C \right)$, the ring of 
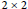$2\,\times \,2$ matrices over $C$, or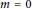 
$m\,=\,0$ and there exists 
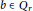$b\,\in \,{{Q}_{r}}$ such that 
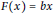$F\left( x \right)\,=\,bx$, for any 
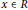$x\,\in \,R$, with 
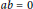$ab\,=\,0$.
