A gap mapping is a discontinuous interval mapping with two strictly increasing branches that have a gap between their ranges. They are one-dimensional dynamical systems, which arise in the study of certain higher dimensional flows, for example the Lorenz flow and the Cherry flow. 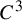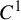In this paper, we prove hyperbolicity of renormalization acting on $C^3$ dissipative gap mappings, and show that the topological conjugacy classes of infinitely renormalizable gap mappings are $C^1$ manifolds.