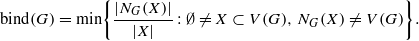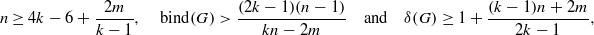Let G be a graph of order n, and let k≥1 be an integer. Let h:E(G)→[0,1] be a function. If ∑ e∋xh(e)=k holds for any x∈V (G), then we call G[Fh] a fractional k-factor of G with indicator function h where Fh ={e∈E(G):h(e)>0}. A graph G is called a fractional (k,m) -deleted graph if for every e∈E(H) , there exists a fractional k-factor G[Fh ] of G with indicator function h such that h(e)=0 , where H is any subgraph of G with m edges. The minimum degree of a vertex in G is denoted by δ(G) . For X⊆V (G), NG(X)=⋃ x∈XNG(x) . The binding number of G is defined by 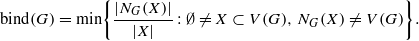In this paper, it is proved that if 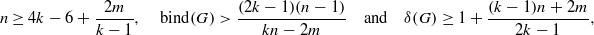then G is a fractional (k,m) -deleted graph. Furthermore, it is shown that this result is best possible in some sense.

Let G be a graph, and k a positive integer. Let h:E(G)→[0,1] be a function. If ∑ e∋xh(e)=k holds for each x∈V (G), then we call G[Fh] a fractional k-factor of G with indicator function h where Fh={e∈E(G)∣h(e)>0}. In this paper we use neighbourhoods to obtain a new sufficient condition for a graph to have a fractional k-factor. Furthermore, this result is shown to be best possible in some sense.