We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We introduce a forcing technique to construct three-dimensional arrays of generic extensions through FS (finite support) iterations of ccc posets, which we refer to as 3D-coherent systems. We use them to produce models of new constellations in Cichoń’s diagram, in particular, a model where the diagram can be separated into 7 different values. Furthermore, we show that this constellation of 7 values is consistent with the existence of a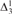 
${\rm{\Delta }}_3^1$ well-order of the reals.
