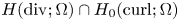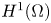We derive a global higher regularity result for weak solutions of the linear relaxed micromorphic model on smooth domains. The governing equations consist of a linear elliptic system of partial differential equations that is coupled with a system of Maxwell-type. The result is obtained by combining a Helmholtz decomposition argument with regularity results for linear elliptic systems and the classical embedding of $H(\operatorname {div};\Omega )\cap H_0(\operatorname {curl};\Omega )$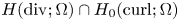 into $H^1(\Omega )$
into $H^1(\Omega )$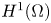 .
.