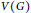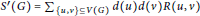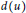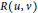1 results
Degree Kirchhoff Index of Bicyclic Graphs
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 1 / 01 March 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 197-205
- Print publication:
- 01 March 2017
-
- Article
-
- You have access
- Export citation
-
Let
$G$ be a connected graph with vertex set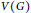 
$V\left( G \right)$.The degree Kirchhoff index of $G$ is defined as 
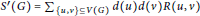${{S}^{\prime }}\left( G \right)\,=\,\sum{_{\left\{ u,v \right\}\,\subseteq \,V\left( G \right)}d\left( u \right)d\left( v \right)R\left( u,\,v \right)}$, where 
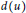$d\left( u \right)$ is the degree of vertex 
$u$, and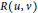 
$R\left( u,\,v \right)$ denotes the resistance distance between vertices $u$ and 
$v$. In this paper, we characterize the graphs having maximum and minimum degree Kirchhoff index among all 
$n$-vertex bicyclic graphs with exactly two cycles.
