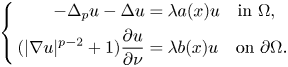1 results
Generalized eigenvalues of the (P, 2)-Laplacian under a parametric boundary condition
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 18 December 2019, pp. 287-303
-
- Article
- Export citation
-
In this paper we study a general eigenvalue problem for the so called (p, 2)-Laplace operator on a smooth bounded domain Ω ⊂ ℝN under a nonlinear Steklov type boundary condition, namely
For positive weight functions a and b satisfying appropriate integrability and boundedness assumptions, we show that, for all p>1, the eigenvalue set consists of an isolated null eigenvalue plus a continuous family of eigenvalues located away from zero.
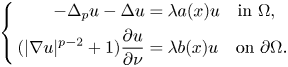\[\left\{ \begin{aligned} -\Delta_pu-\Delta u & =\lambda a(x)u \quad {\rm in}\ \Omega,\\ (|\nabla u|^{p-2}+1)\dfrac{\partial u}{\partial\nu} & =\lambda b(x)u \quad {\rm on}\ \partial\Omega . \end{aligned} \right.\]
