We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We consider a nonlinear elliptic equation of the formdiv [a(∇u)] + F[u] = 0on a domain Ω, subject to a Dirichlet boundary conditiontru = φ. We do not assume that the higher order terma satisfies growth conditions from above. We prove the existence ofcontinuous solutions either when Ω is convex and φ satisfies a one-sidedbounded slope condition, or when a is radial:\hbox{$a(\xi)=\fr{l(|\xi|)}{|\xi|} \xi$}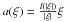
for some increasingl:ℝ+ → ℝ+.
