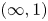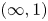1 results
On straightening for Segal spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 23 February 2024, pp. 586-656
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
The straightening–unstraightening correspondence of Grothendieck–Lurie provides an equivalence between cocartesian fibrations between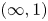
$(\infty, 1)$-categories and diagrams of 
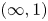$(\infty, 1)$-categories. We provide an alternative proof of this correspondence, as well as an extension of straightening–unstraightening to all higher categorical dimensions. This is based on an explicit combinatorial result relating two types of fibrations between double categories, which can be applied inductively to construct the straightening of a cocartesian fibration between higher categories.
