We introduce and study two conditions on groups of homeomorphisms of Cantor space, namely the conditions of being vigorous and of being flawless. These concepts are dynamical in nature, and allow us to study a certain interplay between the dynamics of an action and the algebraic properties of the acting group. A group 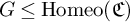 $G\leq \operatorname {Homeo}(\mathfrak {C})$ is vigorous if for any clopen set A and proper clopen subsets B and C of A, there is
$G\leq \operatorname {Homeo}(\mathfrak {C})$ is vigorous if for any clopen set A and proper clopen subsets B and C of A, there is 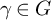 $\gamma \in G$ in the pointwise stabiliser of
$\gamma \in G$ in the pointwise stabiliser of 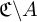 $\mathfrak {C}\backslash A$ with
$\mathfrak {C}\backslash A$ with 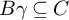 $B\gamma \subseteq C$. A nontrivial group
$B\gamma \subseteq C$. A nontrivial group 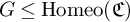 $G\leq \operatorname {Homeo}(\mathfrak {C})$ is flawless if for all k and w a nontrivial freely reduced product expression on k variables (including inverse symbols), a particular subgroup
$G\leq \operatorname {Homeo}(\mathfrak {C})$ is flawless if for all k and w a nontrivial freely reduced product expression on k variables (including inverse symbols), a particular subgroup 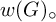 $w(G)_\circ $ of the verbal subgroup
$w(G)_\circ $ of the verbal subgroup 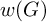 $w(G)$ is the whole group. We show: 1) simple vigorous groups are either two-generated by torsion elements, or not finitely generated, 2) flawless groups are both perfect and lawless, 3) vigorous groups are simple if and only if they are flawless, and, 4) the class of vigorous simple subgroups of
$w(G)$ is the whole group. We show: 1) simple vigorous groups are either two-generated by torsion elements, or not finitely generated, 2) flawless groups are both perfect and lawless, 3) vigorous groups are simple if and only if they are flawless, and, 4) the class of vigorous simple subgroups of 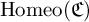 $\operatorname {Homeo}(\mathfrak {C})$ is fairly broad (the class is closed under various natural constructions and contains many well known groups, such as the commutator subgroups of the Higman–Thompson groups
$\operatorname {Homeo}(\mathfrak {C})$ is fairly broad (the class is closed under various natural constructions and contains many well known groups, such as the commutator subgroups of the Higman–Thompson groups 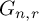 $G_{n,r}$, the Brin-Thompson groups
$G_{n,r}$, the Brin-Thompson groups 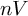 $nV$, Röver’s group
$nV$, Röver’s group 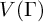 $V(\Gamma )$, and others of Nekrashevych’s ‘simple groups of dynamical origin’).
$V(\Gamma )$, and others of Nekrashevych’s ‘simple groups of dynamical origin’).
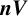 $\boldsymbol {nV}$
$\boldsymbol {nV}$