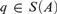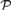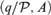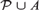1 results
GROUPOIDS AND RELATIVE INTERNALITY
-
- Journal:
- The Journal of Symbolic Logic / Volume 84 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 23 April 2019, pp. 987-1006
- Print publication:
- September 2019
-
- Article
- Export citation
-
In a stable theory, a stationary type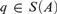
$q \in S\left( A \right)$ internal to a family of partial types 
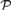${\cal P}$ over A gives rise to a type-definable group, called its binding group. This group is isomorphic to the group 
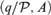$Aut\left( {q/{\cal P},A} \right)$ of permutations of the set of realizations of q, induced by automorphisms of the monster model, fixing 
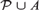${\cal P}\,\mathop \cup \nolimits \,A$ pointwise. In this article, we investigate families of internal types varying uniformly, what we will call relative internality. We prove that the binding groups also vary uniformly, and are the isotropy groups of a natural type-definable groupoid (and even more). We then investigate how properties of this groupoid are related to properties of the type. In particular, we obtain internality criteria for certain 2-analysable types, and a sufficient condition for a type to preserve internality.
