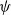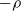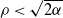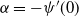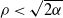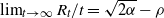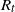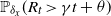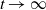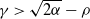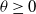1 results
A large deviation theorem for a supercritical super-Brownian motion with absorption
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 02 May 2023, pp. 1249-1274
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
-
We consider a one-dimensional superprocess with a supercritical local branching mechanism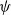
$\psi$, where particles move as a Brownian motion with drift 
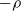$-\rho$ and are killed when they reach the origin. It is known that the process survives with positive probability if and only if 
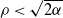$\rho<\sqrt{2\alpha}$, where 
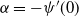$\alpha=-\psi'(0)$. When 
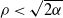$\rho<\sqrt{2 \alpha}$, Kyprianou et al. [18] proved that 
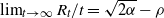$\lim_{t\to \infty}R_t/t =\sqrt{2\alpha}-\rho$ almost surely on the survival set, where 
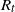$R_t$ is the rightmost position of the support at time t. Motivated by this work, we investigate its large deviation, in other words, the convergence rate of 
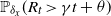$\mathbb{P}_{\delta_x} (R_t >\gamma t+\theta)$ as 
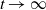$t \to \infty$, where 
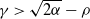$\gamma >\sqrt{2 \alpha} -\rho$, 
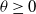$\theta \ge 0$. As a by-product, a related Yaglom-type conditional limit theorem is obtained. Analogous results for branching Brownian motion can be found in Harris et al. [13].
