We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We introduce an intrinsic notion of perimeter for subsets ofa general Minkowski space (i.e. a finite dimensional Banach space in which thenorm is not required to be even).We prove that this notion of perimeter is equivalent tothe usual definition of surface energy for crystals andwe study the regularity properties of the minimizers and the quasi-minimizers of perimeter.In the two-dimensional case we obtain optimal regularity results:apart from a singular set (which is ${\mathcal H}^1$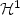 
-negligible and is empty whenthe unit ball is neither a triangle nor a quadrilateral), we find that quasi-minimizers can be locallyparameterized by means of a bi-lipschitz curve, while sets with prescribed bounded curvature are, locally, lipschitz graphs.
