We prove that the statement “there is a k such that for every f there is a k-bounded diagonally nonrecursive function relative to f” does not imply weak König’s lemma over 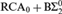 ${\rm{RC}}{{\rm{A}}_0} + {\rm{B\Sigma }}_2^0$. This answers a question posed by Simpson. A recursion-theoretic consequence is that the classic fact that every k-bounded diagonally nonrecursive function computes a 2-bounded diagonally nonrecursive function may fail in the absence of
${\rm{RC}}{{\rm{A}}_0} + {\rm{B\Sigma }}_2^0$. This answers a question posed by Simpson. A recursion-theoretic consequence is that the classic fact that every k-bounded diagonally nonrecursive function computes a 2-bounded diagonally nonrecursive function may fail in the absence of 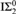 ${\rm{I\Sigma }}_2^0$.
${\rm{I\Sigma }}_2^0$.
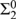 ${\rm{\Sigma }}_2^0$ INDUCTION
${\rm{\Sigma }}_2^0$ INDUCTION