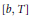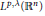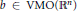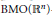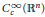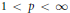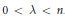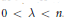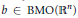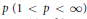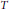In this paper we characterize the compactness of the commutator 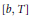 $\left[ b,\,T \right]$ for the singular integral operator on the Morrey spaces
$\left[ b,\,T \right]$ for the singular integral operator on the Morrey spaces 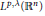 ${{L}^{p,\lambda }}\left( {{\mathbb{R}}^{n}} \right)$. More precisely, we prove that if
${{L}^{p,\lambda }}\left( {{\mathbb{R}}^{n}} \right)$. More precisely, we prove that if 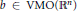 $b\,\in \,\text{VMO}\left( {{\mathbb{R}}^{n}} \right)$, the
$b\,\in \,\text{VMO}\left( {{\mathbb{R}}^{n}} \right)$, the 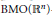 $\text{BMO}\left( {{\mathbb{R}}^{n}} \right)$-closure of
$\text{BMO}\left( {{\mathbb{R}}^{n}} \right)$-closure of 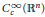 $C_{c}^{\infty }\left( {{\mathbb{R}}^{n}} \right)$, then
$C_{c}^{\infty }\left( {{\mathbb{R}}^{n}} \right)$, then 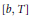 $\left[ b,\,T \right]$ is a compact operator on the Morrey spaces
$\left[ b,\,T \right]$ is a compact operator on the Morrey spaces 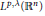 ${{L}^{p,\lambda }}\left( {{\mathbb{R}}^{n}} \right)$ for
${{L}^{p,\lambda }}\left( {{\mathbb{R}}^{n}} \right)$ for 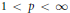 $1\,<\,p\,<\,\infty $ and
$1\,<\,p\,<\,\infty $ and 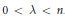 $0\,<\,\lambda \,<\,n$. Conversely, if
$0\,<\,\lambda \,<\,n$. Conversely, if 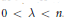 $b\,\in \,\text{BMO}\left( {{\mathbb{R}}^{n}} \right)$ and
$b\,\in \,\text{BMO}\left( {{\mathbb{R}}^{n}} \right)$ and 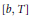 $\left[ b,\,T \right]$ is a compact operator on the
$\left[ b,\,T \right]$ is a compact operator on the 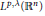 ${{L}^{p,\lambda }}\left( {{\mathbb{R}}^{n}} \right)$ for some
${{L}^{p,\lambda }}\left( {{\mathbb{R}}^{n}} \right)$ for some 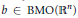 $p\,\left( 1\,<\,p\,<\,\infty \right)$, then
$p\,\left( 1\,<\,p\,<\,\infty \right)$, then 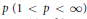 $b\,\in \,\text{VMO}\left( {{\mathbb{R}}^{n}} \right)$. Moreover, the boundedness of a rough singular integral operator
$b\,\in \,\text{VMO}\left( {{\mathbb{R}}^{n}} \right)$. Moreover, the boundedness of a rough singular integral operator 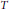 $T$ and its commutator
$T$ and its commutator 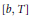 $\left[ b,\,T \right]$ on
$\left[ b,\,T \right]$ on 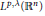 ${{L}^{p,\lambda }}\left( {{\mathbb{R}}^{n}} \right)$ are also given. We obtain a sufficient condition for a subset in Morrey space to be a strongly pre-compact set, which has interest in its own right.
${{L}^{p,\lambda }}\left( {{\mathbb{R}}^{n}} \right)$ are also given. We obtain a sufficient condition for a subset in Morrey space to be a strongly pre-compact set, which has interest in its own right.

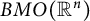
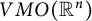
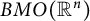
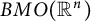
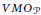
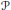
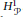

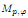 of sublinear operators generated by the parabolic Calderón—Zygmund operator and by the commutator of this operator with bounded mean oscillation (BMO) functions. As a consequence, we obtain a global
of sublinear operators generated by the parabolic Calderón—Zygmund operator and by the commutator of this operator with bounded mean oscillation (BMO) functions. As a consequence, we obtain a global