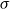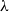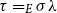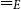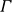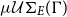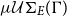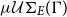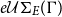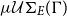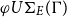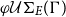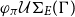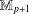Ordering is a well-established concept in mathematics and also plays an important role in many areas of computer science, where quasi-orderings, most notably well-founded quasi-orderings and well-quasi-orderings, are of particular interest. This paper deals with quasi-orderings on first-order terms and introduces a new notion of unification based on a special quasi-order, known as homeomorphic tree embedding. Historically, the development of unification theory began with the central notion of a most general unifier based on the subsumption order. A unifier 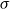 $\sigma$
is most general, if it subsumes any other unifier
$\sigma$
is most general, if it subsumes any other unifier  $\tau$
, that is, if there is a substitution
$\tau$
, that is, if there is a substitution 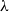 $\lambda$
with
$\lambda$
with 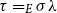 $\tau=_{E}\sigma\lambda$
, where E is an equational theory and
$\tau=_{E}\sigma\lambda$
, where E is an equational theory and 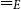 $=_{E}$
denotes equality under E. Since there is in general more than one most general unifier for unification problems under equational theories E, called E-Unification, we have the notion of a complete and minimal set of unifiers under E for a unification problem
$=_{E}$
denotes equality under E. Since there is in general more than one most general unifier for unification problems under equational theories E, called E-Unification, we have the notion of a complete and minimal set of unifiers under E for a unification problem 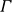 $\varGamma$
, denoted as
$\varGamma$
, denoted as 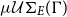 $\mu\mathcal{U}\Sigma_{E}(\Gamma)$
. This set is still the basic notion in unification theory today. But, unfortunately, the subsumption quasi-order is not a well-founded quasi-order, which is the reason why for certain equational theories there are solvable E-unification problems, but the set
$\mu\mathcal{U}\Sigma_{E}(\Gamma)$
. This set is still the basic notion in unification theory today. But, unfortunately, the subsumption quasi-order is not a well-founded quasi-order, which is the reason why for certain equational theories there are solvable E-unification problems, but the set 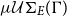 $\mu\mathcal{U}\Sigma_{E}(\Gamma)$
does not exist. They are called type nullary in the unification hierarchy. In order to overcome this problem and also to substantially reduce the number of most general unifiers, we extended the well-known encompassment order on terms to an encompassment order on substitutions (modulo E). Unification under the encompassment order is called essential unification and if
$\mu\mathcal{U}\Sigma_{E}(\Gamma)$
does not exist. They are called type nullary in the unification hierarchy. In order to overcome this problem and also to substantially reduce the number of most general unifiers, we extended the well-known encompassment order on terms to an encompassment order on substitutions (modulo E). Unification under the encompassment order is called essential unification and if 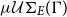 $\mu\mathcal{U}\Sigma_{E}(\Gamma)$
exists, then the complete set of essential unifiers
$\mu\mathcal{U}\Sigma_{E}(\Gamma)$
exists, then the complete set of essential unifiers 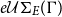 $e\mathcal{U}\Sigma_{E}(\Gamma)$
is a subset of
$e\mathcal{U}\Sigma_{E}(\Gamma)$
is a subset of 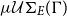 $\mu\mathcal{U}\Sigma_{E}(\Gamma)$
. An interesting effect is that many E-unification problems with an infinite set of most general unifiers (under the subsumption order) reduce to a problem with only finitely many essential unifiers. Moreover, there are cases of an equational theory E, for which the complete set of most general unifiers does not exist, the minimal and complete set of essential unifiers however does exist. Unfortunately again, the encompassment order is not a well-founded quasi-ordering either, that is, there are still theories with a solvable unification problem, for which a minimal and complete set of essential unifiers does not exist. This paper deals with a third approach, namely the extension of the well-known homeomorphic embedding of terms to a homeomorphic embedding of substitutions (modulo E). We examine the set of most general, minimal, and complete E-unifiers under the quasi-order of homeomorphic embedment modulo an equational theory E, called
$\mu\mathcal{U}\Sigma_{E}(\Gamma)$
. An interesting effect is that many E-unification problems with an infinite set of most general unifiers (under the subsumption order) reduce to a problem with only finitely many essential unifiers. Moreover, there are cases of an equational theory E, for which the complete set of most general unifiers does not exist, the minimal and complete set of essential unifiers however does exist. Unfortunately again, the encompassment order is not a well-founded quasi-ordering either, that is, there are still theories with a solvable unification problem, for which a minimal and complete set of essential unifiers does not exist. This paper deals with a third approach, namely the extension of the well-known homeomorphic embedding of terms to a homeomorphic embedding of substitutions (modulo E). We examine the set of most general, minimal, and complete E-unifiers under the quasi-order of homeomorphic embedment modulo an equational theory E, called 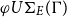 $\varphi U\Sigma_{E}(\Gamma)$
, and propose an appropriate definitional framework based on the standard notions of unification theory extended by notions for the tree embedding theorem or Kruskal’s theorem as it is called. The main results are that for regular theories the minimal and complete set
$\varphi U\Sigma_{E}(\Gamma)$
, and propose an appropriate definitional framework based on the standard notions of unification theory extended by notions for the tree embedding theorem or Kruskal’s theorem as it is called. The main results are that for regular theories the minimal and complete set 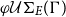 $\varphi\mathcal{U}\Sigma_{E}(\Gamma)$
always exists. If we restrict the E-embedding order to pure E-embedding, a well-known technique in logic programming and term rewriting where the difference between variables is ignored, the set
$\varphi\mathcal{U}\Sigma_{E}(\Gamma)$
always exists. If we restrict the E-embedding order to pure E-embedding, a well-known technique in logic programming and term rewriting where the difference between variables is ignored, the set 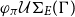 $\varphi_{\pi}\mathcal{U}\Sigma_{E}(\Gamma)$
always exists and it is even finite for any theory E.
$\varphi_{\pi}\mathcal{U}\Sigma_{E}(\Gamma)$
always exists and it is even finite for any theory E.
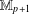 $\mathbb{M}_{p+1}$
$\mathbb{M}_{p+1}$