Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
  1. Home
  2. Search

Refine search

Refine search

Access:
Content type:
Publication date:
Apply   From and To filters
Subject: Show more
Journals Show more
Publishers: Show more
Societies Show more
Series: Show more
Collections: Show more

Actions for selected content:

Select all | Deselect all
  • View selected items
  • Export citations
  • Download PDF (zip)
  • Save to Kindle
  • Save to Dropbox
  • Save to Google Drive

Save Search

You can save your searches here and later view and run them again in "My saved searches".

Please provide a title, maximum of 40 characters.
Cancel
×

1 results

  • Convolution Orthogonality and the Jacobi Polynominals

  • Wm. R. Allaway
  • Journal:
    Canadian Mathematical Bulletin / Volume 32 / Issue 3 / 01 September 1989
    Published online by Cambridge University Press:
    20 November 2018, pp. 298-308
    Print publication:
    01 September 1989
    • Article
      • You have access
    • PDF
    • Export citation

  • Let α and β be any two real numbers and let 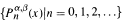be the Jacobi polynomial sequences. For any non-zero real number a, 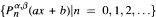is an orthogonal polynomial sequence with respect to convolution if and only if either (i) b = 1, α = 0 and β + 1 is not equal to a negative integer or (ii) b = — 1, β = 0 and α + 1 is not equal to a negative integer.