We consider a critical discrete-time branching process with generation dependent immigration. For the case in which the mean number of immigrating individuals tends to ∞ with the generation number, we prove functional limit theorems for centered and normalized processes. The limiting processes are deterministically time-changed Wiener, with three different covariance functions depending on the behavior of the mean and variance of the number of immigrants. As an application, we prove that the conditional least-squares estimator of the offspring mean is asymptotically normal, which demonstrates an alternative case of normality of the estimator for the process with nondegenerate offspring distribution. The norming factor is 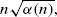 where α(n) denotes the mean number of immigrating individuals in the nth generation.
where α(n) denotes the mean number of immigrating individuals in the nth generation.

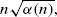 where α(
where α(