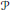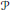For every polytope $\mathcal{P}$ there is the universal regular polytope of the same rank as $\mathcal{P}$ corresponding to the Coxeter group 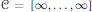$\mathcal{C}\,=\,\left[ \infty ,\,.\,.\,.\,,\,\infty \right]$. For a given automorphism $d$ of 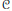$\mathcal{C}$, using monodromy groups, we construct a combinatorial structure 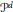${{P}^{d}}$. When 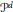${{P}^{d}}$ is a polytope isomorphic to 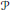$\mathcal{P}$ we say that 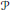$\mathcal{P}$ is self-invariant with respect to $d$, or $d$-invariant. We develop algebraic tools for investigating these operations on polytopes, and in particular give a criterion on the existence of a $d$-automorphism of a given order. As an application, we analyze properties of self-dual edge-transitive polyhedra and polyhedra with two flag-orbits. We investigate properties of medials of such polyhedra. Furthermore, we give an example of a self-dual equivelar polyhedron which contains no polarity (duality of order 2). We also extend the concept of Petrie dual to higher dimensions, and we show how it can be dealt with using self-invariance.

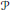
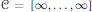
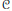
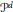
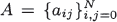The paper characterizes matrices which have a given system of vectors orthogonal with respect to a given probability distribution as its right eigenvectors. Results of Hoare and Rahman are unified in this context, then all matrices with a given orthogonal polynomial system as right eigenvectors under the constraint a0j = 0 for j ≥ 2 are specified. The only stochastic matrices P = {pij} satisfying p00 + p01 = 1 with the Hahn polynomials as right eigenvectors have the form of the Moran mutation model.