Forster [‘Finite-to-one maps’, J. Symbolic Logic68 (2003), 1251–1253] showed, in Zermelo–Fraenkel set theory, that if there is a finite-to-one map from 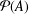 ${\mathcal{P}}(A)$, the set of all subsets of a set
${\mathcal{P}}(A)$, the set of all subsets of a set 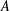 $A$, onto
$A$, onto 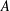 $A$, then
$A$, then 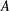 $A$ must be finite. If we assume the axiom of choice (AC), the cardinalities of
$A$ must be finite. If we assume the axiom of choice (AC), the cardinalities of 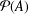 ${\mathcal{P}}(A)$ and the set
${\mathcal{P}}(A)$ and the set 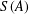 $S(A)$ of permutations on
$S(A)$ of permutations on 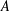 $A$ are equal for any infinite set
$A$ are equal for any infinite set 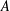 $A$. In the absence of AC, we cannot make any conclusion about the relationship between the two cardinalities for an arbitrary infinite set. In this paper, we give a condition that makes Forster’s theorem, with
$A$. In the absence of AC, we cannot make any conclusion about the relationship between the two cardinalities for an arbitrary infinite set. In this paper, we give a condition that makes Forster’s theorem, with 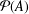 ${\mathcal{P}}(A)$ replaced by
${\mathcal{P}}(A)$ replaced by 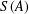 $S(A)$, provable without AC.
$S(A)$, provable without AC.