1 results
A limit theorem for sample maxima and heavy branches in Galton–Watson trees
-
- Journal:
- Journal of Applied Probability / Volume 17 / Issue 2 / June 1980
- Published online by Cambridge University Press:
- 14 July 2016, pp. 539-545
- Print publication:
- June 1980
-
- Article
- Export citation
-
Let Yn be the maximum of n independent positive random variables with common distribution function F and let Sn be their sum. Then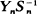
converges to zero in probability if and only if 
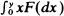is slowly varying. This result implies that in a supercritical Galton-Watson process which does not become extinct, there cannot be a sequence {τ n} of particles, each descended from the preceding one, such that the fraction of all particles which are descendants of τ n does not converge to zero as n →∞. Weakly m-adic trees, which behave to some extent like sample Galton-Watson trees, can have such sequences of particles.
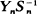converges to zero in probability if and only if 
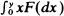is slowly varying. This result implies that in a supercritical Galton-Watson process which does not become extinct, there cannot be a sequence {