In a multiplication module, prime submodules have the following property: if a prime submodule contains a finite intersection of submodules, then one of the submodules is contained in the prime submodule. In this paper, we generalize this property to infinite intersection of submodules and call such prime submodules strongly prime submodules. A multiplication module in which every prime submodule is strongly prime will be called a strongly 0-dimensional module. It is also an extension of strongly 0-dimensional rings. After this we investigate properties of strongly 0-dimensional modules and give relations of von Neumann regular modules, 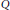 $Q$-modules and strongly 0-dimensional modules.
$Q$-modules and strongly 0-dimensional modules.