Let Sk, l(Γ, ω, χ) be the space of mixed cusp forms of type (k, l) associated to a Fuchsian group Γ, a holomorphic map ω: ℋ → ℋ of the upper half plane into itself and a homomorphism χ: Γ → SL(2, R) such that ω and χ are equivariant. We construct a map from Sk, l(Γ, ω, χ) to the parabolic cohomology space of Γ with coefficients in some Γ-module and prove that this map is injective.
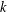 $k$
$k$