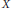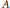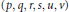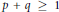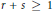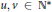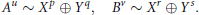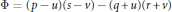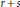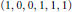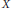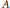Let $X$ and $Y$ be Banach spaces isomorphic to complemented subspaces of each other with supplements $A$ and $B$. In 1996, W. T. Gowers solved the Schroeder–Bernstein (or Cantor–Bernstein) problem for Banach spaces by showing that 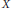$X$ is not necessarily isomorphic to $Y$. In this paper, we obtain a necessary and sufficient condition on the sextuples 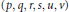$\left( p,\,q,\,r,\,s,\,u,\,v \right)$ in 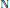$\mathbb{N}$ with 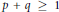$p\,+\,q\,\ge \,1$, 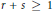$r+s\ge 1$ and 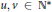$u,\,v\,\in \,{{\mathbb{N}}^{*}}$, to provide that 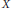$X$ is isomorphic to $Y$, whenever these spaces satisfy the following decomposition scheme

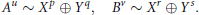$${{A}^{u}}\,\sim \,{{X}^{p}}\,\oplus \,{{Y}^{q}},\,{{B}^{v}}\,\sim \,{{X}^{r}}\,\oplus \,{{Y}^{s}}.$$

Namely, 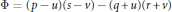$\Phi \,=\,\left( p\,-\,u \right)\left( s\,-\,v \right)-\left( q\,+\,u \right)\left( r\,+\,v \right)$ is different from zero and 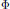$\Phi $ divides 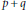$p\,+\,q$ and 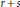$r\,+\,s$. These sextuples are called Cantor–Bernstein sextuples for Banach spaces. The simplest case 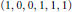$\left( 1,0,0,1,1,1 \right)$ indicates the well-known Pełczyński's decomposition method in Banach space. On the other hand, by interchanging some Banach spaces in the above decomposition scheme, refinements of the Schroeder– Bernstein problem become evident.