We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We prove the existence of a one-parameter family of nearly parallel G2-structures on the manifold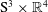 
$\text{S}^{3}\times \mathbb{R}^{4}$, which are mutually non-isomorphic and invariant under the cohomogeneity one action of the group SU(2)3. This family connects the two locally homogeneous nearly parallel G2-structures that are induced by the homogeneous ones on the sphere S7.
