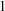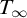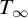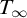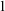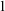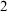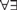We introduce a family of local ranks 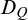 $D_Q$ depending on a finite set Q of pairs of the form
$D_Q$ depending on a finite set Q of pairs of the form 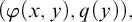 $(\varphi (x,y),q(y)),$ where
$(\varphi (x,y),q(y)),$ where 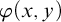 $\varphi (x,y)$ is a formula and
$\varphi (x,y)$ is a formula and 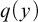 $q(y)$ is a global type. We prove that in any NSOP
$q(y)$ is a global type. We prove that in any NSOP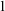 $_1$ theory these ranks satisfy some desirable properties; in particular,
$_1$ theory these ranks satisfy some desirable properties; in particular, 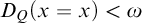 $D_Q(x=x)<\omega $ for any finite tuple of variables x and any Q, if
$D_Q(x=x)<\omega $ for any finite tuple of variables x and any Q, if 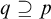 $q\supseteq p$ is a Kim-forking extension of types, then
$q\supseteq p$ is a Kim-forking extension of types, then 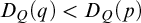 $D_Q(q)<D_Q(p)$ for some Q, and if
$D_Q(q)<D_Q(p)$ for some Q, and if 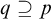 $q\supseteq p$ is a Kim-non-forking extension, then
$q\supseteq p$ is a Kim-non-forking extension, then 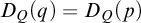 $D_Q(q)=D_Q(p)$ for every Q that involves only invariant types whose Morley powers are
$D_Q(q)=D_Q(p)$ for every Q that involves only invariant types whose Morley powers are 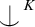 -stationary. We give natural examples of families of invariant types satisfying this property in some NSOP
-stationary. We give natural examples of families of invariant types satisfying this property in some NSOP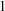 $_1$ theories.
$_1$ theories.
We also answer a question of Granger about equivalence of dividing and dividing finitely in the theory 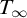 $T_\infty $ of vector spaces with a generic bilinear form. We conclude that forking equals dividing in
$T_\infty $ of vector spaces with a generic bilinear form. We conclude that forking equals dividing in 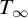 $T_\infty $, strengthening an earlier observation that
$T_\infty $, strengthening an earlier observation that 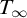 $T_\infty $ satisfies the existence axiom for forking independence.
$T_\infty $ satisfies the existence axiom for forking independence.
Finally, we slightly modify our definitions and go beyond NSOP $_1$ to find out that our local ranks are bounded by the well-known ranks: the inp-rank (burden), and hence, in particular, by the dp-rank. Therefore, our local ranks are finite provided that the dp-rank is finite, for example, if T is dp-minimal. Hence, our notion of rank identifies a non-trivial class of theories containing all NSOP
$_1$ to find out that our local ranks are bounded by the well-known ranks: the inp-rank (burden), and hence, in particular, by the dp-rank. Therefore, our local ranks are finite provided that the dp-rank is finite, for example, if T is dp-minimal. Hence, our notion of rank identifies a non-trivial class of theories containing all NSOP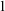 $_1$ and NTP
$_1$ and NTP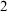 $_2$ theories.
$_2$ theories.
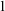 $_1$ THEORIES
$_1$ THEORIES

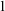
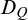
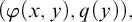
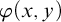
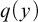
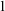
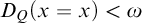
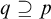
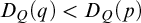
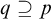
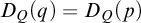
 -stationary. We give natural examples of families of invariant types satisfying this property in some NSOP
-stationary. We give natural examples of families of invariant types satisfying this property in some NSOP