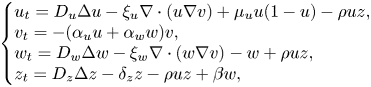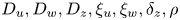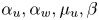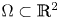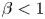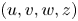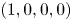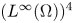1 results
Asymptotic behaviour in a doubly haptotactic cross-diffusion model for oncolytic virotherapy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 19 April 2022, pp. 881-906
- Print publication:
- June 2023
-
- Article
-
- You have access
- HTML
- Export citation
-
This paper considers a model for oncolytic virotherapy given by the doubly haptotactic cross-diffusion system
\[ \left\{\begin{array}{@{}ll} u_t=D_u\Delta u-\xi_u\nabla\cdot(u\nabla v)+\mu_u u(1-u)-\rho uz,\\ v_t={-} (\alpha_u u+\alpha_w w)v,\\ w_t=D_w\Delta w-\xi_w\nabla\cdot(w\nabla v)- w+\rho uz,\\ z_t=D_z\Delta z-\delta_z z- \rho uz+\beta w, \end{array}\right. \]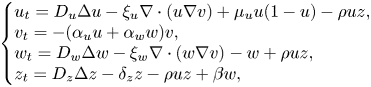with positive parameters $D_u,D_w,D_z,\xi _u,\xi _w,\delta _z,\rho$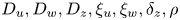
, $\alpha _u,\alpha _w,\mu _u,\beta$
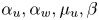. When posed under no-flux boundary conditions in a smoothly bounded domain $\Omega \subset {\mathbb {R}}^{2}$
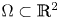, and along with initial conditions involving suitably regular data, the global existence of classical solution to this system was asserted in Tao and Winkler (2020, J. Differ. Equ. 268, 4973–4997). Based on the suitable quasi-Lyapunov functional, it is shown that when the virus replication rate $\beta <1$
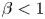, the global classical solution $(u,v,w,z)$
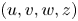is uniformly bounded and exponentially stabilizes to the constant equilibrium $(1, 0, 0, 0)$
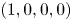in the topology $(L^{\infty }(\Omega ))^{4}$
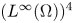as $t\rightarrow \infty$
.
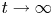