Published online by Cambridge University Press: 19 April 2022
This paper considers a model for oncolytic virotherapy given by the doubly haptotactic cross-diffusion system
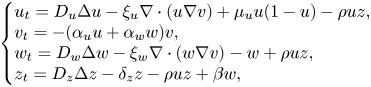
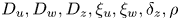 , $\alpha _u,\alpha _w,\mu _u,\beta$
, $\alpha _u,\alpha _w,\mu _u,\beta$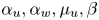 . When posed under no-flux boundary conditions in a smoothly bounded domain $\Omega \subset {\mathbb {R}}^{2}$
. When posed under no-flux boundary conditions in a smoothly bounded domain $\Omega \subset {\mathbb {R}}^{2}$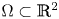 , and along with initial conditions involving suitably regular data, the global existence of classical solution to this system was asserted in Tao and Winkler (2020, J. Differ. Equ. 268, 4973–4997). Based on the suitable quasi-Lyapunov functional, it is shown that when the virus replication rate $\beta <1$
, and along with initial conditions involving suitably regular data, the global existence of classical solution to this system was asserted in Tao and Winkler (2020, J. Differ. Equ. 268, 4973–4997). Based on the suitable quasi-Lyapunov functional, it is shown that when the virus replication rate $\beta <1$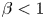 , the global classical solution $(u,v,w,z)$
, the global classical solution $(u,v,w,z)$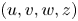 is uniformly bounded and exponentially stabilizes to the constant equilibrium $(1, 0, 0, 0)$
is uniformly bounded and exponentially stabilizes to the constant equilibrium $(1, 0, 0, 0)$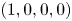 in the topology $(L^{\infty }(\Omega ))^{4}$
in the topology $(L^{\infty }(\Omega ))^{4}$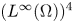 as $t\rightarrow \infty$
as $t\rightarrow \infty$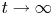 .
.