This article establishes a sufficient condition for Kobayashi hyperbolicity of unbounded domains in terms of curvature. Specifically, when 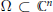 $\Omega \,\subset \,{{\mathbb{C}}^{n}}$ corresponds to a sub-level set of a smooth, real-valued function Ψ such that the form
$\Omega \,\subset \,{{\mathbb{C}}^{n}}$ corresponds to a sub-level set of a smooth, real-valued function Ψ such that the form 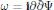 $\omega \,=\,\mathbf{i}\partial \bar{\partial }\Psi $ is Kähler and has bounded curvature outside a bounded subset, then this domain admits a hermitian metric of strictly negative holomorphic sectional curvature.
$\omega \,=\,\mathbf{i}\partial \bar{\partial }\Psi $ is Kähler and has bounded curvature outside a bounded subset, then this domain admits a hermitian metric of strictly negative holomorphic sectional curvature.