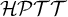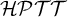1 results
HYBRID PARTIAL TYPE THEORY
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 May 2023, pp. 1-43
-
- Article
-
- You have access
- HTML
- Export citation
-
In this article we define a logical system called Hybrid Partial Type Theory (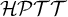
$\mathcal {HPTT}$). The system is obtained by combining William Farmer’s partial type theory with a strong form of hybrid logic. William Farmer’s system is a version of Church’s theory of types which allows terms to be non-denoting; hybrid logic is a version of modal logic in which it is possible to name worlds and evaluate expressions with respect to particular worlds. We motivate this combination of ideas in the introduction, and devote the rest of the article to defining, axiomatising, and proving a completeness result for 
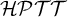$\mathcal {HPTT}$.
