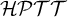1 Introduction
In this article we define a logical system called Hybrid Partial Type Theory (
![]() $\mathcal {HPTT}$
). The system is obtained by combining William Farmer’s partial type theory [Reference Farmer10, Reference Farmer, Benzmueller, Brown and Siekmann11] with a strong form of hybrid logic [Reference Areces, ten Cate, Blackburn, van Benthem and Wolter4, Reference Blackburn5, Reference Indrzejczak18]. William Farmer’s system is a version of Church’s theory of types which allows terms to be non-denoting; hybrid logic is a version of modal logic in which it is possible to name worlds and evaluate expressions with respect to particular worlds. The present article is the latest in a series of articles which attempt to explore the consequences of using Henkin techniques to combine Church’s theory of types with hybrid logic [Reference Areces, Blackburn, Huertas and Manzano2, Reference Areces, Blackburn, Manzano and Huertas3, Reference Blackburn, Huertas, Manzano, Jørgensen, Manzano, Sain and Alonso6].
$\mathcal {HPTT}$
). The system is obtained by combining William Farmer’s partial type theory [Reference Farmer10, Reference Farmer, Benzmueller, Brown and Siekmann11] with a strong form of hybrid logic [Reference Areces, ten Cate, Blackburn, van Benthem and Wolter4, Reference Blackburn5, Reference Indrzejczak18]. William Farmer’s system is a version of Church’s theory of types which allows terms to be non-denoting; hybrid logic is a version of modal logic in which it is possible to name worlds and evaluate expressions with respect to particular worlds. The present article is the latest in a series of articles which attempt to explore the consequences of using Henkin techniques to combine Church’s theory of types with hybrid logic [Reference Areces, Blackburn, Huertas and Manzano2, Reference Areces, Blackburn, Manzano and Huertas3, Reference Blackburn, Huertas, Manzano, Jørgensen, Manzano, Sain and Alonso6].
The motivation for these previous articles was simple. Henkin’s [Reference Henkin16] celebrated article on axiomatising Church’s simple type theory gave logicians a powerful technique for proving completeness results in higher-order logic. Moreover, one of the central themes in the literature on hybrid completeness theory (see, for example, [Reference Blackburn and ten Cate8]) is the use of the Henkin-style model constructions. It was natural to ask whether their mutual reliance on Henkin techniques would enable simple type theory and hybrid logic to be fitted neatly together, and in three previous articles (namely [Reference Areces, Blackburn, Huertas and Manzano2, Reference Blackburn, Huertas, Manzano, Jørgensen, Manzano, Sain and Alonso6, Reference Manzano, Martins and Huertas19]) we showed that this was possible. However—viewed from a modal perspective—an important question remained. These articles used a constant domain semantics: that is, the entities (both first-order and higher-order) over which the quantifiers ranged were the same in all worlds. What happens when we have a varying domain semantics, that is, when the entities over which the quantifiers range may vary from world to world?
It is far from clear what “varying domain semantics” should mean in higher-order modal logic. For first-order modal logic it is straightforward: in a constant domain semantics, at every world we quantify over the same set of individuals. That is, there is a global domain of individuals. In a varying domain semantics, on the other hand, the set of individuals at each world may vary: the domain of individuals is local. So in the first-order case it is easy to define the difference, and indeed, it is possible to prove that either approach can mimic the other (see Proposition 4.8.2 and Theorem 8.8.2 in [Reference Fitting and Mendelsohn14]Footnote 1 ). Matters are more complex in the higher-order case. The key question is: what functions should count as “local”? Here are two (extreme) possibilities. We might try working with the Church-style function hierarchy constructed over the individuals in the union of all local domains. But this would mean that we are working with a varying domain semantics only for individuals—for all higher types, we would effectively have a constant domain semantics. On the other extreme, we could construct a separate Church-style function hierarchy over the individuals in each local domain.
Neither of these two extremes appeal to us. Rather, we will make the following choice: A function is local to a world w if it is only defined on elements of w. But then, the important thing to note is that this idea will demand that we make use of a semantics that can handle partiality, which is why we make use of Farmer’s partial version of Church’s simple theory of types [Reference Church9] (for our approach to partiality in first-order hybrid logic, see [Reference Blackburn, Martins, Manzano and Huertas7]).
1.1 Structure of the article
In Section 2 we present the syntax and semantics of
![]() $\mathcal {HPTT}$
. In Section 3 we explain how our work is related to Farmer’s version of Church’s type theory which allows partial functions as members of the type hierarchy. In Section 4 we define a set of rigid expressions which will play a key role in our model construction, and note some useful lemmas on variable substitution and other topics. In Section 5 we discuss existence, denotation, the various definitions of equality that are natural in a partial framework, and the “hierarchy of falsities” that we make use of. In Section 6 we present our axiomatization. In Section 7 we define the saturated maximal consistent sets that we use in our model construction, and prove some important lemmas about them. In Section 8 we use a Lindenbaum-style construction to build the saturated maximal consistent saturated sets that we need, and then, in Section 9, we show how they can be used to build a model. We put the pieces together in Section 10, where we show that this model yields a Henkin-style completeness proof for our axiomatisation. Section 11 concludes.
$\mathcal {HPTT}$
. In Section 3 we explain how our work is related to Farmer’s version of Church’s type theory which allows partial functions as members of the type hierarchy. In Section 4 we define a set of rigid expressions which will play a key role in our model construction, and note some useful lemmas on variable substitution and other topics. In Section 5 we discuss existence, denotation, the various definitions of equality that are natural in a partial framework, and the “hierarchy of falsities” that we make use of. In Section 6 we present our axiomatization. In Section 7 we define the saturated maximal consistent sets that we use in our model construction, and prove some important lemmas about them. In Section 8 we use a Lindenbaum-style construction to build the saturated maximal consistent saturated sets that we need, and then, in Section 9, we show how they can be used to build a model. We put the pieces together in Section 10, where we show that this model yields a Henkin-style completeness proof for our axiomatisation. Section 11 concludes.
2 Hybrid Partial Type Theory
We first introduce the syntax of
![]() $\mathcal {HPTT}$
(the types and kinds it uses and its meaningful expressions) and then its semantics (a hybrid logical semantics defined using a Farmer-style partial/total valuation approach).
$\mathcal {HPTT}$
(the types and kinds it uses and its meaningful expressions) and then its semantics (a hybrid logical semantics defined using a Farmer-style partial/total valuation approach).
2.1 Syntax
We first define the types (and kinds) of
![]() $\mathcal {HPTT}$
, and then the meaningful expressions of each type.
$\mathcal {HPTT}$
, and then the meaningful expressions of each type.
Definition 2.1 (Types and kinds of
 $\mathcal {HPTT}$
).
$\mathcal {HPTT}$
).
Let t and e be different symbols. The following three sets are defined recursively:
-
•
 $\mathsf {TYPES} ::=t\mid e\mid \langle a,b \rangle $
, where
$\mathsf {TYPES} ::=t\mid e\mid \langle a,b \rangle $
, where
 $a,b\in \mathsf {TYPES}$
and
$a,b\in \mathsf {TYPES}$
and
 $a \not =t$
, is the set of types of
$a \not =t$
, is the set of types of
 $\mathcal {HPTT}$
. We will often write
$\mathcal {HPTT}$
. We will often write
 $ab$
instead of
$ab$
instead of
 $\langle a,b \rangle $
when no confusion arises.
$\langle a,b \rangle $
when no confusion arises. -
•
 $\mathsf {KIND}_t:= t \mid \langle a,b \rangle $
, where
$\mathsf {KIND}_t:= t \mid \langle a,b \rangle $
, where
 $a\in \mathsf {TYPES}$
and
$a\in \mathsf {TYPES}$
and
 $b\in \mathsf {KIND}_t$
. This subset of
$b\in \mathsf {KIND}_t$
. This subset of
 $\mathsf {TYPES}$
is the set of types of kind t .
$\mathsf {TYPES}$
is the set of types of kind t . -
•
 $\mathsf {KIND}_e:= e \mid \langle a,b \rangle $
, where
$\mathsf {KIND}_e:= e \mid \langle a,b \rangle $
, where
 $a \in \mathsf {TYPES}$
and
$a \in \mathsf {TYPES}$
and
 $b\in \mathsf {KIND}_e$
. This subset of
$b\in \mathsf {KIND}_e$
. This subset of
 $\mathsf {TYPES}$
is the set of types of kind e.
$\mathsf {TYPES}$
is the set of types of kind e.
Clearly
![]() $\mathsf {KIND}_e\cup \mathsf {KIND}_t= \mathsf {TYPES}$
.
$\mathsf {KIND}_e\cup \mathsf {KIND}_t= \mathsf {TYPES}$
.
We call e the type of individuals, and t the type of truth values. Formally
![]() $\langle a,b \rangle \in \mathsf {KIND}_t$
will be the types of total functions from elements of type a to elements of type
$\langle a,b \rangle \in \mathsf {KIND}_t$
will be the types of total functions from elements of type a to elements of type
![]() $b $
(where b is of kind t); informally, they should be thought of as the types of predicates and formulas. Formally
$b $
(where b is of kind t); informally, they should be thought of as the types of predicates and formulas. Formally
![]() $\langle a,b \rangle \in \mathsf {KIND}_e$
will be the types of possibly partial functions from elements of type a to elements of type b (where b is of kind e); informally, they should be thought of as the type of functions and terms.
$\langle a,b \rangle \in \mathsf {KIND}_e$
will be the types of possibly partial functions from elements of type a to elements of type b (where b is of kind e); informally, they should be thought of as the type of functions and terms.
Definition 2.2 (Meaningful expressions of
 $\mathcal {HPTT}$
).
$\mathcal {HPTT}$
).
The set
![]() $\mathsf {ME}_a$
of meaningful expressions of type a consists of the basic and complex expressions of type a.
$\mathsf {ME}_a$
of meaningful expressions of type a consists of the basic and complex expressions of type a.
-
• Basic Expressions: For each type
 $a\not =t$
,
$a\not =t$
,
 $\mathcal {HPTT}$
contains a countable set of constants
$\mathcal {HPTT}$
contains a countable set of constants
 $c_{n,a}$
and a denumerably infinite set of variables,
$c_{n,a}$
and a denumerably infinite set of variables,
 $v_{n,a}$
, where n is a natural number. The set of all constants of type a is called
$v_{n,a}$
, where n is a natural number. The set of all constants of type a is called
 $\mathsf {CON}_{a}$
and the set of all variables of type a is called
$\mathsf {CON}_{a}$
and the set of all variables of type a is called
 $\mathsf {VAR}_{a} $
. We define
$\mathsf {VAR}_{a} $
. We define
 $\mathsf {CON}$
and
$\mathsf {CON}$
and
 $\mathsf {VAR}$
to be the set of all constants and the set of all of variables, respectively.In addition, for type t, we have:
$\mathsf {VAR}$
to be the set of all constants and the set of all of variables, respectively.In addition, for type t, we have:-
(1) the two special logical symbols
 $\top $
and
$\top $
and
 $\bot $
;
$\bot $
; -
(2) a countable set
 $\mathsf {NOM}$
of nominals
$\mathsf {NOM}$
of nominals
 $i_{n}$
, n a natural number;
$i_{n}$
, n a natural number; -
(3) a denumerably infinite set
 $\mathsf {SVAR}$
of state variables
$\mathsf {SVAR}$
of state variables
 $s_{n}$
, with n a natural number.
$s_{n}$
, with n a natural number.
We define
 $\mathsf {HYB}$
to be
$\mathsf {HYB}$
to be
 $\mathsf {NOM}\cup \mathsf {SVAR}$
.
$\mathsf {NOM}\cup \mathsf {SVAR}$
.Summing up, as basic expressions we have:
 $$ \begin{align*} &\top \in \mathsf{ME}:{t}\mid \bot \in \mathsf{ME}:{t}\mid i_{n}\in \mathsf{ME}:{t}\mid s_{n}\in \mathsf{ME}:{t}\mid c_{n,a}\\&\quad\in \mathsf{ME}:{a}\mid v_{n,a}\in \mathsf{ME}:{a}. \end{align*} $$
$$ \begin{align*} &\top \in \mathsf{ME}:{t}\mid \bot \in \mathsf{ME}:{t}\mid i_{n}\in \mathsf{ME}:{t}\mid s_{n}\in \mathsf{ME}:{t}\mid c_{n,a}\\&\quad\in \mathsf{ME}:{a}\mid v_{n,a}\in \mathsf{ME}:{a}. \end{align*} $$
-
-
• Complex Expressions: These are recursively generated as follows:
where $$ \begin{gather*} (\gamma _{ba}\beta _{b})\in \mathsf{ME}:{a}\mid \left\langle \lambda u_{b}\alpha _{a}\right\rangle \in \mathsf{ME}:{ba}\mid (@_{i}\alpha _{a})\in \mathsf{ME}:{a}\mid (@_{s}\alpha _{a})\in \mathsf{ME}_{a}, \\ \{(\alpha _{a}\equiv \delta _{a}),\,(\lnot \varphi ),\,(\varphi \wedge \psi ),\,(\forall u_{b}\varphi ),\,(\square \varphi ),\,(\mathsf{A}\varphi ),\ ({ {\downarrow\hspace{-0.1 pt}} \ }s\varphi )\}\subseteq \mathsf{ME}:{t}, \end{gather*} $$
$$ \begin{gather*} (\gamma _{ba}\beta _{b})\in \mathsf{ME}:{a}\mid \left\langle \lambda u_{b}\alpha _{a}\right\rangle \in \mathsf{ME}:{ba}\mid (@_{i}\alpha _{a})\in \mathsf{ME}:{a}\mid (@_{s}\alpha _{a})\in \mathsf{ME}_{a}, \\ \{(\alpha _{a}\equiv \delta _{a}),\,(\lnot \varphi ),\,(\varphi \wedge \psi ),\,(\forall u_{b}\varphi ),\,(\square \varphi ),\,(\mathsf{A}\varphi ),\ ({ {\downarrow\hspace{-0.1 pt}} \ }s\varphi )\}\subseteq \mathsf{ME}:{t}, \end{gather*} $$
 $\gamma _{ba}\in \mathsf {ME}_{ba}$
,
$\gamma _{ba}\in \mathsf {ME}_{ba}$
,
 $\beta _{b}\in \mathsf {ME}_{b}$
,
$\beta _{b}\in \mathsf {ME}_{b}$
,
 $u_{b}$
is a variable of type b,
$u_{b}$
is a variable of type b,
 $\alpha _{a}$
and
$\alpha _{a}$
and
 $\delta _{a}$
are in
$\delta _{a}$
are in
 $\mathsf {ME}_{a}$
,
$\mathsf {ME}_{a}$
,
 $i\in \mathsf {NOM}$
,
$i\in \mathsf {NOM}$
,
 $s\in \mathsf {SVAR}$
, and
$s\in \mathsf {SVAR}$
, and
 $\varphi $
and
$\varphi $
and
 $\psi $
are in
$\psi $
are in
 $\mathsf {ME}_{t}$
.
$\mathsf {ME}_{t}$
.
We will usually explicitly give the type of a meaningful expression, writing
![]() $\alpha _a$
to emphasize that
$\alpha _a$
to emphasize that
![]() $\alpha _a\in \mathsf {ME}_a$
. Moreover, we often call expressions of type t formulas and use the symbols
$\alpha _a\in \mathsf {ME}_a$
. Moreover, we often call expressions of type t formulas and use the symbols
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
to emphasize that they are formulas. The remaining Booleans are defined in the usual way, and the existential quantifier
$\psi $
to emphasize that they are formulas. The remaining Booleans are defined in the usual way, and the existential quantifier
![]() $\exists x\varphi $
, the diamond
$\exists x\varphi $
, the diamond
![]() $\Diamond \varphi $
, and the diamond form of the existential modality
$\Diamond \varphi $
, and the diamond form of the existential modality
![]() $\mathsf {E}\varphi $
are defined as
$\mathsf {E}\varphi $
are defined as
![]() $\lnot \forall x\lnot \varphi $
,
$\lnot \forall x\lnot \varphi $
,
![]() $\lnot \Box \lnot \varphi $
, and
$\lnot \Box \lnot \varphi $
, and
![]() $\lnot \mathsf {A}\lnot \varphi $
, respectively. We routinely drop outermost brackets, and drop others when no confusion arises.
$\lnot \mathsf {A}\lnot \varphi $
, respectively. We routinely drop outermost brackets, and drop others when no confusion arises.
2.2 Semantics
Our partial semantics is based on partial functions, so we first introduce the basic terminology and notation we will use when working with them. Given non-empty sets A and B, we write
![]() $f:A\rightsquigarrow B$
to say that f is a partial function with domain A and range B. The partial functions from A to B can be regarded as total functions with domain A and range
$f:A\rightsquigarrow B$
to say that f is a partial function with domain A and range B. The partial functions from A to B can be regarded as total functions with domain A and range
![]() $B\cup \{\divideontimes \}$
, with
$B\cup \{\divideontimes \}$
, with
![]() $\divideontimes $
an arbitrary object that belongs neither to A nor to B (in what follows, we fix the symbol
$\divideontimes $
an arbitrary object that belongs neither to A nor to B (in what follows, we fix the symbol
![]() $ \divideontimes $
to express lack of denotation or undefinedness). We write
$ \divideontimes $
to express lack of denotation or undefinedness). We write
![]() $ \mathsf {PF}(A,B)$
for the set of all partial functions from A to
$ \mathsf {PF}(A,B)$
for the set of all partial functions from A to
![]() $ B $
, so
$ B $
, so
![]() $\mathsf {PF}(A,B)=\left \{ f\mid f:A\rightsquigarrow B\right \} $
. For
$\mathsf {PF}(A,B)=\left \{ f\mid f:A\rightsquigarrow B\right \} $
. For
![]() $f\in \mathsf {PF}(A,B)$
we write
$f\in \mathsf {PF}(A,B)$
we write
![]() $\mathit {Def} (f)=\{a\in A\mid \text {there exists } b\in B \text { and } f(a)=b\}$
.
$\mathit {Def} (f)=\{a\in A\mid \text {there exists } b\in B \text { and } f(a)=b\}$
.
There are two special cases of partial functions from A to B, namely the empty function, which is the unique function such that
![]() $Def(f)=\varnothing $
, and the total functions
$Def(f)=\varnothing $
, and the total functions
![]() $f:A\to B$
, which are the ones such that
$f:A\to B$
, which are the ones such that
![]() $Def(f)=A$
.
$Def(f)=A$
.
Definition 2.3 (Skeleton).
![]() $\mathcal {S}=\langle \langle \mathsf {D}_a \rangle _{a\in \mathsf {TYPES}},W,R, \langle \mathsf {D}^w_a \rangle _{\langle w,a \rangle \in W\times \mathsf {TYPES}} \rangle $
is a skeleton, where:
$\mathcal {S}=\langle \langle \mathsf {D}_a \rangle _{a\in \mathsf {TYPES}},W,R, \langle \mathsf {D}^w_a \rangle _{\langle w,a \rangle \in W\times \mathsf {TYPES}} \rangle $
is a skeleton, where:
-
(1)
 $\langle \mathsf {D}_a \rangle _{a\in \mathsf {TYPES}}$
is a partial type hierarchy, defined recursively as follows:
$\langle \mathsf {D}_a \rangle _{a\in \mathsf {TYPES}}$
is a partial type hierarchy, defined recursively as follows:-
(a)
 $\mathsf {D}_t=\{T,F\}$
is the set of truth values.
$\mathsf {D}_t=\{T,F\}$
is the set of truth values. -
(b)
 $\mathsf {D}_e=A \not =\varnothing $
is the set of individuals, such that
$\mathsf {D}_e=A \not =\varnothing $
is the set of individuals, such that
 $\divideontimes \not \in \mathsf {D}_e$
.
$\divideontimes \not \in \mathsf {D}_e$
. -
(c) For
 $\left \langle a,b\right \rangle \in \mathsf {KIND}_{e}$
,
$\left \langle a,b\right \rangle \in \mathsf {KIND}_{e}$
,
 $ \mathsf {D}_{ab}$
is a non-empty subset of the set
$ \mathsf {D}_{ab}$
is a non-empty subset of the set
 $\mathsf {PF}( \mathsf {D}_{a},\mathsf {D}_{b})$
of partial functions from
$\mathsf {PF}( \mathsf {D}_{a},\mathsf {D}_{b})$
of partial functions from
 $\mathsf {D}_{a}$
into
$\mathsf {D}_{a}$
into
 $\mathsf {D}_{b}$
. That is:
$\mathsf {D}_{b}$
. That is:
 $\varnothing \not =\mathsf {D}_{ab}\subseteq \mathsf {PF}(\mathsf {D}_{a}, \mathsf {D}_{b})=\{f\mid f:\mathsf {D}_{a}\rightsquigarrow \mathsf {D}_{b}\}.$
$\varnothing \not =\mathsf {D}_{ab}\subseteq \mathsf {PF}(\mathsf {D}_{a}, \mathsf {D}_{b})=\{f\mid f:\mathsf {D}_{a}\rightsquigarrow \mathsf {D}_{b}\}.$
-
(d) For
 $\left \langle a,b\right \rangle \in \mathsf {KIND}_{t}$
,
$\left \langle a,b\right \rangle \in \mathsf {KIND}_{t}$
,
 $ \mathsf {D}_{ab}$
is a non-empty subset of the set
$ \mathsf {D}_{ab}$
is a non-empty subset of the set
 $\mathsf {D}_{b}^{\mathsf {D} _{a}}$
of all total functions from
$\mathsf {D}_{b}^{\mathsf {D} _{a}}$
of all total functions from
 $\mathsf {D}_{a}$
into
$\mathsf {D}_{a}$
into
 $\mathsf {D}_{b}$
.
$\mathsf {D}_{b}$
.
-
-
(2)
 $W\not =\varnothing $
is the set of worlds.
$W\not =\varnothing $
is the set of worlds. -
(3)
 $R\subseteq W\times W$
is the accessibility relation.
$R\subseteq W\times W$
is the accessibility relation. -
(4)
 $\langle \mathsf {D}_{a}^{w}\rangle _{\langle w,a \rangle \in W\times \mathsf {TYPES}}$
are the local domains in the hierarchy. The universes
$\langle \mathsf {D}_{a}^{w}\rangle _{\langle w,a \rangle \in W\times \mathsf {TYPES}}$
are the local domains in the hierarchy. The universes
 $\mathsf {D}_{a}^{w}$
are built as follows:
$\mathsf {D}_{a}^{w}$
are built as follows:-
(a)
 $\varnothing \not =\mathsf {D}^w_e\subseteq \mathsf {D}_e$
is the universe of individuals of world w and
$\varnothing \not =\mathsf {D}^w_e\subseteq \mathsf {D}_e$
is the universe of individuals of world w and
 $\mathsf {D}_e=\bigcup \limits _{w\in W}\mathsf {D}^w_e$
.
$\mathsf {D}_e=\bigcup \limits _{w\in W}\mathsf {D}^w_e$
. -
(b)
 $\mathsf {D}^w_t=\{T,F\}$
is the set of truth values of world
$\mathsf {D}^w_t=\{T,F\}$
is the set of truth values of world
 $ w$
.
$ w$
. -
(c) For
 $\left \langle a,b\right \rangle \in \mathsf {KIND}_{e}$
,
$\left \langle a,b\right \rangle \in \mathsf {KIND}_{e}$
,
 $ \mathsf {D}_{ab}^{w}=\left \{ f\in \mathsf {D}_{ab}\mid \mathit {Def} (f)\subseteq \mathsf {D}_{a}^{w}\right \} $
. That is, for a
$ \mathsf {D}_{ab}^{w}=\left \{ f\in \mathsf {D}_{ab}\mid \mathit {Def} (f)\subseteq \mathsf {D}_{a}^{w}\right \} $
. That is, for a
 $\mathsf {KIND}_{e}$
function f to belong to a local domain, it can only be defined on elements of
$\mathsf {KIND}_{e}$
function f to belong to a local domain, it can only be defined on elements of
 $\mathsf {D}_{a}^{w}$
. We call this the locality for kind e condition.
$\mathsf {D}_{a}^{w}$
. We call this the locality for kind e condition. -
(d) For
 $\left \langle a,b\right \rangle \in \mathsf {KIND}_{t}$
,
$\left \langle a,b\right \rangle \in \mathsf {KIND}_{t}$
,
 $ \mathsf {D}_{ab}^{w}=\{f\in \mathsf {D}_{ab}\mid f(\theta )=F_{b}$
for all
$ \mathsf {D}_{ab}^{w}=\{f\in \mathsf {D}_{ab}\mid f(\theta )=F_{b}$
for all
 $ \theta \in \mathsf {D}_{a}-\mathsf {D}_{a}^{w}\}$
. The function
$ \theta \in \mathsf {D}_{a}-\mathsf {D}_{a}^{w}\}$
. The function
 $F_{b}$
can be thought of as meaning “falsity for type b expressions.”These “falsity functions” are inductively defined (for any type b of kind t) by:
$F_{b}$
can be thought of as meaning “falsity for type b expressions.”These “falsity functions” are inductively defined (for any type b of kind t) by:
 $(1) \ F_{t}=F$
and
$(1) \ F_{t}=F$
and
 $(2) \ F_{ab}(\theta )=F_{b}$
for any
$(2) \ F_{ab}(\theta )=F_{b}$
for any
 $\theta \in \mathsf {D}_{a}$
. So for a
$\theta \in \mathsf {D}_{a}$
. So for a
 $\mathsf {KIND}_{t}$
function f to belong to a local domain
$\mathsf {KIND}_{t}$
function f to belong to a local domain
 $\mathsf {D}_{ab}^{w}$
, it must return the value
$\mathsf {D}_{ab}^{w}$
, it must return the value
 $ F_{b}$
for all the elements not in
$ F_{b}$
for all the elements not in
 $\mathsf {D}_{a}^{w}$
. That is: if
$\mathsf {D}_{a}^{w}$
. That is: if
 $ f(a)\not =F_{b}$
then
$ f(a)\not =F_{b}$
then
 $a\in \mathsf {D}_{a}^{w}$
. We call this the locality for kind t condition.
$a\in \mathsf {D}_{a}^{w}$
. We call this the locality for kind t condition.
-
Note that
![]() $\mathsf {D}_{ab}^{w}\subseteq \mathsf {D}_{ab}$
for all
$\mathsf {D}_{ab}^{w}\subseteq \mathsf {D}_{ab}$
for all
![]() $\langle a,b \rangle \in \mathsf {TYPES}$
and
$\langle a,b \rangle \in \mathsf {TYPES}$
and
![]() $\divideontimes \not \in \mathsf {D} _a $
, for any
$\divideontimes \not \in \mathsf {D} _a $
, for any
![]() $a\in \mathsf {TYPES}$
.
$a\in \mathsf {TYPES}$
.
As the skeleton’s definition shows, our partial type hierarchy distinguishes between kind e and t types. We also allow local domains for all types, as we want a varying domain semantics in the aforementioned sense. Moreover, we require that at the initial level the domain of truth values contains just T and F, and the same happens for all the local domains of type t; we have two truth values in all worlds.
Definition 2.4 (Interpretation function).
![]() $\mathsf {I}$
is an interpretation function whose domain is
$\mathsf {I}$
is an interpretation function whose domain is
![]() $\{\top ,\bot \}\cup \mathsf {NOM}\cup \mathsf {CON}$
.
$\{\top ,\bot \}\cup \mathsf {NOM}\cup \mathsf {CON}$
.
![]() $\mathsf {I}$
assigns to each symbol in this set a function from W to the domains of the partial type hierarchy of appropriate types. We impose some constraints on what counts as a legitimate interpretation function. In particular:
$\mathsf {I}$
assigns to each symbol in this set a function from W to the domains of the partial type hierarchy of appropriate types. We impose some constraints on what counts as a legitimate interpretation function. In particular:
-
(1)
 $\mathsf {I}(\top )$
and
$\mathsf {I}(\top )$
and
 $\mathsf {I}(\bot )$
are total functions from W to
$\mathsf {I}(\bot )$
are total functions from W to
 $\{T,F\} $
. As we want
$\{T,F\} $
. As we want
 $\top $
and
$\top $
and
 $\bot $
to be rigid logical names for truth and falsehood respectively, we demand that for any world
$\bot $
to be rigid logical names for truth and falsehood respectively, we demand that for any world
 $w\in W$
,
$w\in W$
,
 $ \left [ \mathsf {I}(\top )\right ] (w)=T$
and
$ \left [ \mathsf {I}(\top )\right ] (w)=T$
and
 $\left [ \mathsf {I}(\bot )\right ] (w)=F$
.
$\left [ \mathsf {I}(\bot )\right ] (w)=F$
. -
(2) As we want nominals to act like names for worlds, we demand that for all nominals i,
 $\mathsf {I}(i)$
is a total function with domain W and range
$\mathsf {I}(i)$
is a total function with domain W and range
 $\left \{ T,F\right \}$
such that
$\left \{ T,F\right \}$
such that
 $\left [ \mathsf {I}(i)\right ] (w)=T$
for a unique
$\left [ \mathsf {I}(i)\right ] (w)=T$
for a unique
 $w\in W$
. The nominal “names” the (unique) world it is true at.
$w\in W$
. The nominal “names” the (unique) world it is true at. -
(3) For any constant
 $c_a$
with
$c_a$
with
 $a\in \mathsf {KIND}_t$
, we define
$a\in \mathsf {KIND}_t$
, we define
 $ \mathsf {I}(c_a)$
to be a total function from W to
$ \mathsf {I}(c_a)$
to be a total function from W to
 $\mathsf {D}_a$
.
$\mathsf {D}_a$
. -
(4) For any constant
 $c_a$
with
$c_a$
with
 $a\in \mathsf {KIND}_e$
, we define
$a\in \mathsf {KIND}_e$
, we define
 $ \mathsf {I}(c_a)$
to be a partial function from W to
$ \mathsf {I}(c_a)$
to be a partial function from W to
 $\mathsf {D}_a$
(that is, an element of
$\mathsf {D}_a$
(that is, an element of
 $\mathsf {PF}(W,\mathsf {D}_a)$
; recall that
$\mathsf {PF}(W,\mathsf {D}_a)$
; recall that
 $ \divideontimes $
has been fixed such that
$ \divideontimes $
has been fixed such that
 $\divideontimes \not \in \mathsf {D} _a $
, for all types a). Moreover:
$\divideontimes \not \in \mathsf {D} _a $
, for all types a). Moreover:-
(a) As we want every constant to denote in at least one world, we demand that
 $[\mathsf {I}(c_a)] (w)\not =\divideontimes $
for at least one world
$[\mathsf {I}(c_a)] (w)\not =\divideontimes $
for at least one world
 $w\in W$
.
$w\in W$
. -
(b) As we want anything that any constant denotes at any world to exist at some world, we demand that for any constant
 $c_{a}$
and world w, if
$c_{a}$
and world w, if
 $[\mathsf {I}(c_{a})](w)\not =\divideontimes $
then
$[\mathsf {I}(c_{a})](w)\not =\divideontimes $
then
 $[\mathsf {I}(c_{a})](w)\in \mathsf {D}_{a}^{v}$
for at least one world
$[\mathsf {I}(c_{a})](w)\in \mathsf {D}_{a}^{v}$
for at least one world
 $v\in W$
.
$v\in W$
.
-
Definition 2.5 (
 $\mathcal {HPTT}$
models).
$\mathcal {HPTT}$
models).
A structure (or model) for
![]() $\mathcal {HPTT}$
is a pair
$\mathcal {HPTT}$
is a pair
![]() $\mathcal {M}=\langle \mathcal {S},\mathsf {I} \rangle $
, where
$\mathcal {M}=\langle \mathcal {S},\mathsf {I} \rangle $
, where
![]() $ \mathcal {S}$
is a skeleton and I is an interpretation.
$ \mathcal {S}$
is a skeleton and I is an interpretation.
We will return to the two constraints imposed on constants
![]() $c_{a}$
of
$c_{a}$
of
![]() $\mathsf {KIND}_{e}$
later in the article, when we present formulas
$\mathsf {KIND}_{e}$
later in the article, when we present formulas
![]() $\mathsf {EXISTS}(c_{a})$
and
$\mathsf {EXISTS}(c_{a})$
and
![]() $\mathsf {DEN}(c_{a})$
expressing “
$\mathsf {DEN}(c_{a})$
expressing “
![]() $c_{a}$
exists” and “
$c_{a}$
exists” and “
![]() $c_{a}$
denotes” respectively (see Definition 5.1). Here we will simply remark that our structures are built in a number of local features. For a start, they have varying domains:
$c_{a}$
denotes” respectively (see Definition 5.1). Here we will simply remark that our structures are built in a number of local features. For a start, they have varying domains:
![]() $\mathsf {D}_{e}^{w}$
, the universe of individuals of world w, may vary without restriction from world to world; thus type e (first-order) existence is treated as an intrinsically local affair. But we also have locality when it comes to higher-order entities. Clause (4)(c) of the previous Definition 2.3 insists that a type
$\mathsf {D}_{e}^{w}$
, the universe of individuals of world w, may vary without restriction from world to world; thus type e (first-order) existence is treated as an intrinsically local affair. But we also have locality when it comes to higher-order entities. Clause (4)(c) of the previous Definition 2.3 insists that a type
![]() $\left \langle a,b\right \rangle $
function of kind e can only belong to a local domain
$\left \langle a,b\right \rangle $
function of kind e can only belong to a local domain
![]() $ \mathsf {D}_{ab}^{w}$
when all the entities on which it is defined belong to
$ \mathsf {D}_{ab}^{w}$
when all the entities on which it is defined belong to
![]() $ \mathsf {D}_{a}^{w}$
as well. Moreover, although functions of kind t are total, Clause (4)(d) gives them a local flavour too: when any such function is applied at any world to an element outside the local domain, the result is a “falsity function” of the appropriate type.
$ \mathsf {D}_{a}^{w}$
as well. Moreover, although functions of kind t are total, Clause (4)(d) gives them a local flavour too: when any such function is applied at any world to an element outside the local domain, the result is a “falsity function” of the appropriate type.
Before going further, we note the following special class of functions in
![]() $ \mathcal {HPTT}$
models. We will see that all functions in the hierarchy of falsities
$ \mathcal {HPTT}$
models. We will see that all functions in the hierarchy of falsities
![]() $\left \langle F_{a}\right \rangle _{a\in \mathsf {KIND} _{t}}$
satisfy the locality for kind t condition and so are good candidates for a member of the local domains.
$\left \langle F_{a}\right \rangle _{a\in \mathsf {KIND} _{t}}$
satisfy the locality for kind t condition and so are good candidates for a member of the local domains.
Proposition 2.6. Let
![]() $\mathcal {M}$
be a structure such that
$\mathcal {M}$
be a structure such that
![]() $F_{c}\in \mathsf {D}_{c}$
for all
$F_{c}\in \mathsf {D}_{c}$
for all
![]() $c\in \mathsf {KIND}_{t}$
. Then
$c\in \mathsf {KIND}_{t}$
. Then
![]() $F_{c}\in \mathsf {D}_{c}^{w}$
for all
$F_{c}\in \mathsf {D}_{c}^{w}$
for all
![]() $c\in \mathsf {KIND}_{t}$
and all
$c\in \mathsf {KIND}_{t}$
and all
![]() $w \in W$
.
$w \in W$
.
Proof Let
![]() $\mathcal {M}$
be a structure such that
$\mathcal {M}$
be a structure such that
![]() $F_{c}\in \mathsf {D}_{c}$
for all
$F_{c}\in \mathsf {D}_{c}$
for all
![]() $c\in \mathsf {KIND}_{t}$
. In the first place,
$c\in \mathsf {KIND}_{t}$
. In the first place,
![]() $F_{t}=F$
and
$F_{t}=F$
and
![]() $\mathsf {D }_{t}^{w}=\left \{ T,F\right \} $
, by condition 4(b) of Definition 2.3. Moreover,
$\mathsf {D }_{t}^{w}=\left \{ T,F\right \} $
, by condition 4(b) of Definition 2.3. Moreover,
![]() $\mathsf {D}_{ab}^{w}=\{f\in \mathsf {D}_{ab}\mid f(\theta )=F_{b}$
for all
$\mathsf {D}_{ab}^{w}=\{f\in \mathsf {D}_{ab}\mid f(\theta )=F_{b}$
for all
![]() $\theta \in \mathsf {D}_{a}-\mathsf {D}_{a}^{w}\}$
(by definition), and
$\theta \in \mathsf {D}_{a}-\mathsf {D}_{a}^{w}\}$
(by definition), and
![]() $F_{ab}(\theta )=F_{b}$
for all
$F_{ab}(\theta )=F_{b}$
for all
![]() $\theta \in \mathsf {D} _{a}$
(by Definition 2.3, Clause (4)(d)). Therefore,
$\theta \in \mathsf {D} _{a}$
(by Definition 2.3, Clause (4)(d)). Therefore,
![]() $F_{ab}\in \mathsf {D}_{ab}^{w}$
for all
$F_{ab}\in \mathsf {D}_{ab}^{w}$
for all
![]() $\left \langle a,b\right \rangle \in \mathsf {KIND}_{t}$
.
$\left \langle a,b\right \rangle \in \mathsf {KIND}_{t}$
.
Definition 2.7. An assignment g is a function with domain
![]() $ \mathsf {VAR}\cup \mathsf {SVAR}$
such that
$ \mathsf {VAR}\cup \mathsf {SVAR}$
such that
![]() $g(v_{a})\in \mathsf { D}_{a}$
for
$g(v_{a})\in \mathsf { D}_{a}$
for
![]() $v_{a}\in \mathsf {VAR}$
, and
$v_{a}\in \mathsf {VAR}$
, and
![]() $g(s)\in W$
for
$g(s)\in W$
for
![]() $s\in \mathsf {SVAR}$
.
$s\in \mathsf {SVAR}$
.
An assignment
![]() $g^{\prime }$
is a v-variant of g if it coincides with g on all values except, perhaps, on the value assigned to
$g^{\prime }$
is a v-variant of g if it coincides with g on all values except, perhaps, on the value assigned to
![]() $v\in \mathsf {VAR}$
. We use
$v\in \mathsf {VAR}$
. We use
![]() $g_{v}^{\theta }$
to denote the v-variant of g whose value for
$g_{v}^{\theta }$
to denote the v-variant of g whose value for
![]() $v\in \mathsf {VAR}_{a}$
is
$v\in \mathsf {VAR}_{a}$
is
![]() $\theta \in \mathsf {D}_{a}$
. Similarly,
$\theta \in \mathsf {D}_{a}$
. Similarly,
![]() $g^{\prime }$
is an s-variant of g if it coincides with g on all values except, perhaps, on the value assigned to
$g^{\prime }$
is an s-variant of g if it coincides with g on all values except, perhaps, on the value assigned to
![]() $s\in \mathsf {SVAR}$
. We use
$s\in \mathsf {SVAR}$
. We use
![]() $g_{s}^{w}$
to denote the s-variant of g whose value for s is
$g_{s}^{w}$
to denote the s-variant of g whose value for s is
![]() $w\in W$
.
$w\in W$
.
Definition 2.8 (Interpretations).
An interpretation for
![]() $\mathcal {HPTT}$
is a pair
$\mathcal {HPTT}$
is a pair
![]() $\langle \mathcal {M},g\rangle $
, where
$\langle \mathcal {M},g\rangle $
, where
![]() $\mathcal {M}$
is a structure for
$\mathcal {M}$
is a structure for
![]() $\mathcal {HPTT}$
and g is an assignment of values to variables.
$\mathcal {HPTT}$
and g is an assignment of values to variables.
Definition 2.9 (General interpretations).
Let
![]() $\mathcal { M}$
be a structure such that:
$\mathcal { M}$
be a structure such that:
-
•
 $\mathsf {\divideontimes }\notin \mathsf {D}_{a}$
for all
$\mathsf {\divideontimes }\notin \mathsf {D}_{a}$
for all
 $a\in \mathsf { TYPES}$
,
$a\in \mathsf { TYPES}$
, -
•
 $F_{a}\in \mathsf {D}_{a}$
for all
$F_{a}\in \mathsf {D}_{a}$
for all
 $a\in \mathsf {KIND}_{t}$
(which by Proposition 2.6 tells us that
$a\in \mathsf {KIND}_{t}$
(which by Proposition 2.6 tells us that
 $F_{a}\in \mathsf {D} _{a}^{w}$
for all
$F_{a}\in \mathsf {D} _{a}^{w}$
for all
 $a\in \mathsf {KIND}_{t}$
and all
$a\in \mathsf {KIND}_{t}$
and all
 $w \in W$
),
$w \in W$
), -
•
 $\bigcup \limits _{w\in W}\mathsf {D}^w_a=\mathsf {D}_a$
, for any
$\bigcup \limits _{w\in W}\mathsf {D}^w_a=\mathsf {D}_a$
, for any
 $a\in \mathsf { TYPES}$
,
$a\in \mathsf { TYPES}$
,
and let g be any assignment on this structure. We now recursively define for any expression
![]() $\alpha $
the interpretation
$\alpha $
the interpretation
![]() $[[\alpha ]]^{\mathcal {M},w,g}$
of
$[[\alpha ]]^{\mathcal {M},w,g}$
of
![]() $\alpha $
with respect to
$\alpha $
with respect to
![]() $\langle \mathcal {M},g \rangle $
at the world w. We will say that
$\langle \mathcal {M},g \rangle $
at the world w. We will say that
![]() $\langle \mathcal {M },g \rangle $
is a general interpretation if the following conditions are satisfied:
$\langle \mathcal {M },g \rangle $
is a general interpretation if the following conditions are satisfied:
-
• If
 $a\in \mathsf {KIND}_e$
, then
$a\in \mathsf {KIND}_e$
, then
 $[[\alpha _a]]^{\mathcal {M} ,w,g}\in \mathsf {D}_a\cup \{\divideontimes \}$
.
$[[\alpha _a]]^{\mathcal {M} ,w,g}\in \mathsf {D}_a\cup \{\divideontimes \}$
. -
• If
 $a\in \mathsf {KIND}_t$
, then
$a\in \mathsf {KIND}_t$
, then
 $[[\alpha _a]]^{\mathcal {M} ,w,g}\in \mathsf {D}_a$
.
$[[\alpha _a]]^{\mathcal {M} ,w,g}\in \mathsf {D}_a$
.
In addition, the following conditions should hold for the definition of
![]() $[[\alpha _a]]^{\mathcal {M},w,g}$
:
$[[\alpha _a]]^{\mathcal {M},w,g}$
:
-
(1)
 $[[i]]^{\mathcal {M},w,g}=\left [ \mathsf {I}(i)\right ] (w)$
, for any
$[[i]]^{\mathcal {M},w,g}=\left [ \mathsf {I}(i)\right ] (w)$
, for any
 $ i\in \mathsf {NOM}$
.
$ i\in \mathsf {NOM}$
. -
(2)
 $[[c_a]]^{\mathcal {M},w,g}=\left [ \mathsf {I}(c_a)\right ] (w)$
, for any
$[[c_a]]^{\mathcal {M},w,g}=\left [ \mathsf {I}(c_a)\right ] (w)$
, for any
 $c_a\in \mathsf {CON}_a$
.
$c_a\in \mathsf {CON}_a$
. -
(3)
 $[[v_a]]^{\mathcal {M},w,g}=g(v_a)$
, for any
$[[v_a]]^{\mathcal {M},w,g}=g(v_a)$
, for any
 $v_a\in \mathsf {VAR}_a$
.
$v_a\in \mathsf {VAR}_a$
. -
(4)
 $[[s]]^{\mathcal {M},w,g}=T$
if
$[[s]]^{\mathcal {M},w,g}=T$
if
 $g(s)=w$
and
$g(s)=w$
and
 $[[s]]^{\mathcal {M},w,g}=F$
if
$[[s]]^{\mathcal {M},w,g}=F$
if
 $g(s)\not =w$
, for
$g(s)\not =w$
, for
 $s\in \mathsf {SVAR}$
.
$s\in \mathsf {SVAR}$
. -
(5)
 $[[\top ]]^{\mathcal {M},w,g}=\left [ \mathsf {I}(\top )\right ] (w)$
(where
$[[\top ]]^{\mathcal {M},w,g}=\left [ \mathsf {I}(\top )\right ] (w)$
(where
 $\left [ \mathsf {I}(\top )\right ] (w)=T$
for all
$\left [ \mathsf {I}(\top )\right ] (w)=T$
for all
 $w\in W$
).
$w\in W$
). -
(6)
 $[[\bot ]]^{\mathcal {M},w,g}=\left [ \mathsf {I}(\bot )\right ] (w)$
(where
$[[\bot ]]^{\mathcal {M},w,g}=\left [ \mathsf {I}(\bot )\right ] (w)$
(where
 $\left [ \mathsf {I}(\bot )\right ] (w)=F$
for all
$\left [ \mathsf {I}(\bot )\right ] (w)=F$
for all
 $w\in W$
).
$w\in W$
). -
(7) The definition of
 $[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M},w,g}$
has two cases, one for each kind:
$[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M},w,g}$
has two cases, one for each kind:-
(a)
 $\left \langle b,a\right \rangle \in \mathsf {KIND}_{t}$
.
$\left \langle b,a\right \rangle \in \mathsf {KIND}_{t}$
.
 $ [[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M},w,g}=h$
, where h is the function from
$ [[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M},w,g}=h$
, where h is the function from
 $\mathsf {D}_{b}$
to
$\mathsf {D}_{b}$
to
 $\mathsf {D}_{a}$
s.t.
$\mathsf {D}_{a}$
s.t.
 $h(\theta )=F_{a}$
when
$h(\theta )=F_{a}$
when
 $\theta \in \mathsf {D}_{b}-\mathsf {D}_{b}^{w}$
and
$\theta \in \mathsf {D}_{b}-\mathsf {D}_{b}^{w}$
and
 $ h(\theta )=[[\alpha _{a}]]^{\mathcal {M},w,g^{\prime }}$
, where
$ h(\theta )=[[\alpha _{a}]]^{\mathcal {M},w,g^{\prime }}$
, where
 $g^{\prime }=g_{u_{b}}^{\theta }$
, otherwise. That is,
$g^{\prime }=g_{u_{b}}^{\theta }$
, otherwise. That is,
 $\lambda $
-expressions of kind
$\lambda $
-expressions of kind
 $ t $
are total functions which satisfy the locality for kind t condition.
$ t $
are total functions which satisfy the locality for kind t condition. -
(b)
 $\left \langle b,a\right \rangle \in \mathsf {KIND}_{e}$
.
$\left \langle b,a\right \rangle \in \mathsf {KIND}_{e}$
.
 $ [[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M},w,g}=h$
, where h is the partial function
$ [[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M},w,g}=h$
, where h is the partial function
 $\mathsf {D}_{b}$
to
$\mathsf {D}_{b}$
to
 $\mathsf {D}_{a}$
s.t.
$\mathsf {D}_{a}$
s.t.
 $h(\theta )=\divideontimes $
when
$h(\theta )=\divideontimes $
when
 $\theta \in \mathsf {D}_{b}-\mathsf {D} _{b}^{w}$
and
$\theta \in \mathsf {D}_{b}-\mathsf {D} _{b}^{w}$
and
 $h(\theta )=[[\alpha _{a}]]^{\mathcal {M},w,g^{\prime }}$
, where
$h(\theta )=[[\alpha _{a}]]^{\mathcal {M},w,g^{\prime }}$
, where
 $g^{\prime }=g_{u_{b}}^{\theta }$
, otherwise. That is,
$g^{\prime }=g_{u_{b}}^{\theta }$
, otherwise. That is,
 $\lambda $
-expressions of kind e are partial functions which satisfy the locality for kind e condition.
$\lambda $
-expressions of kind e are partial functions which satisfy the locality for kind e condition.
-
-
(8) The definition of
 $[[\gamma _{ba}\beta _{b}]]^{\mathcal {M},w,g}$
has two cases, one for each kind:
$[[\gamma _{ba}\beta _{b}]]^{\mathcal {M},w,g}$
has two cases, one for each kind:-
(a)
 $\left \langle b,a\right \rangle \in \mathsf {KIND}_{t}$
. For
$\left \langle b,a\right \rangle \in \mathsf {KIND}_{t}$
. For
 $ \gamma _{ba}$
and
$ \gamma _{ba}$
and
 $\beta _{b}$
: If
$\beta _{b}$
: If
 $[[\beta _{b}]]^{\mathcal {M} ,w,g}\not =\divideontimes $
, then
$[[\beta _{b}]]^{\mathcal {M} ,w,g}\not =\divideontimes $
, then
 $[[\gamma _{ba}\beta _{b}]]^{\mathcal {M} ,w,g}=[[\gamma _{ba}]]^{\mathcal {M},w,g}([[\beta _{b}]]^{\mathcal {M},w,g})$
; otherwise
$[[\gamma _{ba}\beta _{b}]]^{\mathcal {M} ,w,g}=[[\gamma _{ba}]]^{\mathcal {M},w,g}([[\beta _{b}]]^{\mathcal {M},w,g})$
; otherwise
 $[[\gamma _{ba}\beta _{b}]]^{\mathcal {M},w,g}=F_{a}$
. In the first case the result could be
$[[\gamma _{ba}\beta _{b}]]^{\mathcal {M},w,g}=F_{a}$
. In the first case the result could be
 $F_a$
as well because falsity functions are elements of
$F_a$
as well because falsity functions are elements of
 $\mathsf { D}_{a}$
.
$\mathsf { D}_{a}$
. -
(b)
 $\left \langle b,a\right \rangle \in \mathsf {KIND}_{e}$
. For
$\left \langle b,a\right \rangle \in \mathsf {KIND}_{e}$
. For
 $ \gamma _{ba}$
and
$ \gamma _{ba}$
and
 $\beta _{b}$
: If
$\beta _{b}$
: If
 $[[\gamma _{ba}]]^{\mathcal {M} ,w,g}\not =\divideontimes $
,
$[[\gamma _{ba}]]^{\mathcal {M} ,w,g}\not =\divideontimes $
,
 $[[\beta _{b}]]^{\mathcal {M},w,g}\not = \divideontimes $
, then
$[[\beta _{b}]]^{\mathcal {M},w,g}\not = \divideontimes $
, then
 $[[\gamma _{ba}\beta _{b}]]^{\mathcal {M} ,w,g}=[[\gamma _{ba}]]^{\mathcal {M},w,g}([[\beta _{b}]]^{\mathcal {M},w,g})$
; otherwise
$[[\gamma _{ba}\beta _{b}]]^{\mathcal {M} ,w,g}=[[\gamma _{ba}]]^{\mathcal {M},w,g}([[\beta _{b}]]^{\mathcal {M},w,g})$
; otherwise
 $[[\gamma _{ba}\beta _{b}]]^{\mathcal {M},w,g}=\divideontimes $
. In the first case the result could be undefined because functions of kind e are partial.
$[[\gamma _{ba}\beta _{b}]]^{\mathcal {M},w,g}=\divideontimes $
. In the first case the result could be undefined because functions of kind e are partial.
-
-
(9) For any
 $\alpha _{a}$
and
$\alpha _{a}$
and
 $\beta _{a}$
. If both
$\beta _{a}$
. If both
 $[[\alpha _{a}]]^{ \mathcal {M},w,g}$
and
$[[\alpha _{a}]]^{ \mathcal {M},w,g}$
and
 $[[\beta _{a}]]^{\mathcal {M},w,g}$
are different from
$[[\beta _{a}]]^{\mathcal {M},w,g}$
are different from
 $ \divideontimes $
, then
$ \divideontimes $
, then
 $[[\alpha _{a}\equiv \beta _{a}]]^{\mathcal {M},w,g}=T$
if
$[[\alpha _{a}\equiv \beta _{a}]]^{\mathcal {M},w,g}=T$
if
 $[[\alpha _{a}]]^{\mathcal {M},w,g}=[[\beta _{a}]]^{\mathcal {M},w,g}$
; otherwise
$[[\alpha _{a}]]^{\mathcal {M},w,g}=[[\beta _{a}]]^{\mathcal {M},w,g}$
; otherwise
 $[[\alpha _{a}\equiv \beta _{a}]]^{\mathcal {M},w,g}=F$
.
$[[\alpha _{a}\equiv \beta _{a}]]^{\mathcal {M},w,g}=F$
. -
(10)
 $[[\lnot \varphi ]]^{\mathcal {M},w,g}=T$
iff
$[[\lnot \varphi ]]^{\mathcal {M},w,g}=T$
iff
 $[[\varphi ]]^{\mathcal {M} ,w,g}=F$
, for
$[[\varphi ]]^{\mathcal {M} ,w,g}=F$
, for
 $\varphi \in \mathsf {ME}_{t}$
.
$\varphi \in \mathsf {ME}_{t}$
. -
(11)
 $[[\varphi \wedge \psi ]]^{\mathcal {M},w,g}=T$
iff
$[[\varphi \wedge \psi ]]^{\mathcal {M},w,g}=T$
iff
 $[[\varphi ]]^{ \mathcal {M},w,g}=T$
and
$[[\varphi ]]^{ \mathcal {M},w,g}=T$
and
 $[[\psi ]]^{\mathcal {M},w,g}=T$
, for
$[[\psi ]]^{\mathcal {M},w,g}=T$
, for
 $\varphi ,\psi \in \mathsf {ME}_{t}$
.
$\varphi ,\psi \in \mathsf {ME}_{t}$
. -
(12)
 $[[\forall x_a\varphi ]]^{\mathcal {M},w,g}=T$
iff for all
$[[\forall x_a\varphi ]]^{\mathcal {M},w,g}=T$
iff for all
 $\theta \in \mathsf {D}^w_a$
,
$\theta \in \mathsf {D}^w_a$
,
 $[[\varphi ]]^{\mathcal {M},w,h}=T$
, for
$[[\varphi ]]^{\mathcal {M},w,h}=T$
, for
 $x_a\in \mathsf { VAR}_a$
,
$x_a\in \mathsf { VAR}_a$
,
 $\varphi \in \mathsf {ME}_t$
, and
$\varphi \in \mathsf {ME}_t$
, and
 $h=g_{x_a}^{\theta }$
.
$h=g_{x_a}^{\theta }$
. -
(13)
 $[[\Box \varphi ]]^{\mathcal {M},w,g}=T$
iff for all
$[[\Box \varphi ]]^{\mathcal {M},w,g}=T$
iff for all
 $v\in W$
such that
$v\in W$
such that
 $\langle w,v \rangle \in R$
,
$\langle w,v \rangle \in R$
,
 $[[\varphi ]]^{\mathcal {M},v,g}=T$
, for
$[[\varphi ]]^{\mathcal {M},v,g}=T$
, for
 $ \varphi \in \mathsf {ME}_t$
.
$ \varphi \in \mathsf {ME}_t$
. -
(14)
 $[[@_i\alpha _a]]^{\mathcal {M},w,g}=[[\alpha _a]]^{\mathcal {M},v,g}$
where v is the unique element such that
$[[@_i\alpha _a]]^{\mathcal {M},w,g}=[[\alpha _a]]^{\mathcal {M},v,g}$
where v is the unique element such that
 $[\mathsf {I}(i)] (v)=T$
.
$[\mathsf {I}(i)] (v)=T$
. -
(15)
 $[[@_s\alpha _a]]^{\mathcal {M},w,g}=[[\alpha _a]]^{\mathcal {M},v,g}$
, where
$[[@_s\alpha _a]]^{\mathcal {M},w,g}=[[\alpha _a]]^{\mathcal {M},v,g}$
, where
 $v=g(s)$
.
$v=g(s)$
. -
(16)
 $[[{{\downarrow \hspace {-0.1 pt}} }s\varphi ]]^{\mathcal {M},w,g}=T$
iff
$[[{{\downarrow \hspace {-0.1 pt}} }s\varphi ]]^{\mathcal {M},w,g}=T$
iff
 $[[\varphi ]]^{ \mathcal {M},w,g^{\prime }}=T$
, where
$[[\varphi ]]^{ \mathcal {M},w,g^{\prime }}=T$
, where
 $g^{\prime }=g_{s}^{w}$
.
$g^{\prime }=g_{s}^{w}$
. -
(17)
 $[[\mathsf {A}\varphi ]]^{\mathcal {M},w,g}=T$
iff for all
$[[\mathsf {A}\varphi ]]^{\mathcal {M},w,g}=T$
iff for all
 $v\in W$
,
$v\in W$
,
 $ [[\varphi ]]^{\mathcal {M},v,g}=T$
.
$ [[\varphi ]]^{\mathcal {M},v,g}=T$
.
2.2.1 General interpretation insignia.
The important requirement here is that we want our structures to be closed under definability, as is always the case with general structures for type theory. We also demand that, at each level, the union of the local universes be the universe of this level.
Two remarks should be added at this stage. The first is that the definition given above guarantees that we have partial evaluation for expressions of kind e but total evaluation for expressions of kind t. In particular, all formulas denote a standard truth value. More precisely, for any structure
![]() $\mathcal {M}$
, assignment g and world w:
$\mathcal {M}$
, assignment g and world w:
-
• Expressions of kind e : Given a structure
 $\mathcal {M}$
, a world w, and an assignment g, a (non-lambda) expression
$\mathcal {M}$
, a world w, and an assignment g, a (non-lambda) expression
 $\alpha _{a}$
of kind e could be (1) non-denoting (
$\alpha _{a}$
of kind e could be (1) non-denoting (
 $[[\alpha _{a}]]^{\mathcal {M},w,g} \not \in \mathsf {D}_{a}$
), (2) denoting but not existing (
$[[\alpha _{a}]]^{\mathcal {M},w,g} \not \in \mathsf {D}_{a}$
), (2) denoting but not existing (
 $[[\alpha _{a}]]^{\mathcal {M},w,g} \in \mathsf {D}_{a} - \mathsf {D}_{a}^{w}$
), or (3) existing (
$[[\alpha _{a}]]^{\mathcal {M},w,g} \in \mathsf {D}_{a} - \mathsf {D}_{a}^{w}$
), or (3) existing (
 $[[\alpha _{a}]]^{\mathcal {M},w,g} \in \mathsf {D}_{a}^{w}$
). In Section 5, we will express these semantic properties in the object language. It is certainly possible that
$[[\alpha _{a}]]^{\mathcal {M},w,g} \in \mathsf {D}_{a}^{w}$
). In Section 5, we will express these semantic properties in the object language. It is certainly possible that
 $[[\alpha _{a}]]^{\mathcal {M},w,g}=\divideontimes $
, but, for lambda expressions, it holds that
$[[\alpha _{a}]]^{\mathcal {M},w,g}=\divideontimes $
, but, for lambda expressions, it holds that
 $[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M},w,g}\not = \divideontimes $
. In fact, clause (7)(b) in Definition 2.9 guarantees that
$[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M},w,g}\not = \divideontimes $
. In fact, clause (7)(b) in Definition 2.9 guarantees that
 $[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M},w,g}$
is a partial and local function. To see this, note that for all elements
$[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M},w,g}$
is a partial and local function. To see this, note that for all elements
 $\theta \in \mathsf { D}_{b}-\mathsf {D}_{b}^{w}$
,
$\theta \in \mathsf { D}_{b}-\mathsf {D}_{b}^{w}$
,
 $[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M},w,g}(\theta )=\divideontimes $
. So, the function
$[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M},w,g}(\theta )=\divideontimes $
. So, the function
 $[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M },w,g}$
is partial and local. Clause (7)(b) also tells us that for all elements
$[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M },w,g}$
is partial and local. Clause (7)(b) also tells us that for all elements
 $\theta \in \mathsf {D}_{b}^{w}$
,
$\theta \in \mathsf {D}_{b}^{w}$
,
 $[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M},w,g}(\theta )$
is always
$[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M},w,g}(\theta )$
is always
 $ [[\alpha _a]]^{\mathcal {M},w,g^{\ast }}$
(which may well be
$ [[\alpha _a]]^{\mathcal {M},w,g^{\ast }}$
(which may well be
 $\divideontimes $
) where
$\divideontimes $
) where
 $g^{\ast }=g_{u_{b}}^{\theta }$
. Empty functions are a particular case of local functions of kind e as they return
$g^{\ast }=g_{u_{b}}^{\theta }$
. Empty functions are a particular case of local functions of kind e as they return
 $\divideontimes $
for all the arguments.
$\divideontimes $
for all the arguments. -
• Expressions of kind t : For any expression
 $\alpha $
of kind t,
$\alpha $
of kind t,
 $ [[\alpha ]]^{\mathcal {M},w,g}\not =\divideontimes $
. In particular, for expressions of type t, the value is always T or F. Moreover,
$ [[\alpha ]]^{\mathcal {M},w,g}\not =\divideontimes $
. In particular, for expressions of type t, the value is always T or F. Moreover,
 $ [[\left \langle \lambda u_{b}\varphi \right \rangle ]]^{\mathcal {M},w,g}$
is always defined, and it is a total and local function from
$ [[\left \langle \lambda u_{b}\varphi \right \rangle ]]^{\mathcal {M},w,g}$
is always defined, and it is a total and local function from
 $\mathsf {D} _{b}$
to
$\mathsf {D} _{b}$
to
 $\mathsf {D}_{t}$
which returns False (F) on all non-local arguments (see Clause (7)(a) in Definition 2.9). Therefore,
$\mathsf {D}_{t}$
which returns False (F) on all non-local arguments (see Clause (7)(a) in Definition 2.9). Therefore,
 $[[\left \langle \lambda u_{b}\varphi \right \rangle ]]^{\mathcal {M} ,w,g}$
is a perfect candidate for a member of domain
$[[\left \langle \lambda u_{b}\varphi \right \rangle ]]^{\mathcal {M} ,w,g}$
is a perfect candidate for a member of domain
 $\mathsf {D}_{bt}^{w}$
. This is not only true for lambda expressions of type
$\mathsf {D}_{bt}^{w}$
. This is not only true for lambda expressions of type
 $\left \langle a,t\right \rangle $
. In fact, due to the definition, the interpretation of any lambda expression of kind t, say
$\left \langle a,t\right \rangle $
. In fact, due to the definition, the interpretation of any lambda expression of kind t, say
 $[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M},w,g}$
, is a member of the local domain
$[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M},w,g}$
, is a member of the local domain
 $ \mathsf {D}_{ba}^{w}$
. To see this, note that for all elements
$ \mathsf {D}_{ba}^{w}$
. To see this, note that for all elements
 $\theta \in \mathsf {D}_{b}-\mathsf {D}_{b}^{w}$
,
$\theta \in \mathsf {D}_{b}-\mathsf {D}_{b}^{w}$
,
 $[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M},w,g}(\theta )=F_{a}$
. Function
$[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M},w,g}(\theta )=F_{a}$
. Function
 $ \left \langle \lambda x_{a}\top \right \rangle $
of kind t, when interpreted at world w, sends all elements of
$ \left \langle \lambda x_{a}\top \right \rangle $
of kind t, when interpreted at world w, sends all elements of
 $\mathsf {D}_{a}^{w}$
to T while members of
$\mathsf {D}_{a}^{w}$
to T while members of
 $\mathsf {D}_{a}-\mathsf {D}_{a}^{w}$
are sent to F. Therefore, this lambda expression defines local domain
$\mathsf {D}_{a}-\mathsf {D}_{a}^{w}$
are sent to F. Therefore, this lambda expression defines local domain
 $\mathsf {D}_{a}^{w}$
. Another interesting case of local functions of kind t are the falsity functions themselves, which are crucial to our construction.
$\mathsf {D}_{a}^{w}$
. Another interesting case of local functions of kind t are the falsity functions themselves, which are crucial to our construction.Also related to the locality for kind t condition of lambda expressions is the possibility of distinguishing between predicates
 $P_{at}$
and
$P_{at}$
and
 $\langle \lambda x_{a} P_{at} x_{a} \rangle $
.
$\langle \lambda x_{a} P_{at} x_{a} \rangle $
.
 $P_{at} \alpha _{a}$
may be true for denoting non-existing expressions, while
$P_{at} \alpha _{a}$
may be true for denoting non-existing expressions, while
 $\langle \lambda x_{a} P_{at} x_{a} \rangle \alpha _{a}$
demands existence to be true. In other words, the truth of
$\langle \lambda x_{a} P_{at} x_{a} \rangle \alpha _{a}$
demands existence to be true. In other words, the truth of
 $\langle \lambda x_{a} P_{at} x_{a} \rangle \alpha _{a}$
at the world w requires that
$\langle \lambda x_{a} P_{at} x_{a} \rangle \alpha _{a}$
at the world w requires that
 $[[\alpha _{a}]]^{\mathcal {M},w,g} \in \mathsf {D}_{a}^{w}$
(so
$[[\alpha _{a}]]^{\mathcal {M},w,g} \in \mathsf {D}_{a}^{w}$
(so
 $[[\alpha _{a}]]^{\mathcal {M},w,g}$
needs to pass, roughly speaking, a “double checking”: having the property and existing). The calculus counterpart of this distinction is that lambda conversion only works for existing entities.
$[[\alpha _{a}]]^{\mathcal {M},w,g}$
needs to pass, roughly speaking, a “double checking”: having the property and existing). The calculus counterpart of this distinction is that lambda conversion only works for existing entities.
Definition 2.10 (Truth and consequence).
Let
![]() $\Gamma \cup \left \{ \varphi \right \} \subseteq \mathsf {ME}_t$
and
$\Gamma \cup \left \{ \varphi \right \} \subseteq \mathsf {ME}_t$
and
![]() $\mathcal {M}$
be a structure.
$\mathcal {M}$
be a structure.
-
Truth: We say that
 $\mathcal {\varphi }$
is true at the structure
$\mathcal {\varphi }$
is true at the structure
 $ \mathcal {M}$
— written
$ \mathcal {M}$
— written
 $\mathcal {\models }_{\mathcal {M}}\mathcal {\varphi }$
— iff for all
$\mathcal {\models }_{\mathcal {M}}\mathcal {\varphi }$
— iff for all
 $w\in W$
and all assignments g we have that
$w\in W$
and all assignments g we have that
 $[[\varphi ]]^{ \mathcal {M},w,g}=T$
.
$[[\varphi ]]^{ \mathcal {M},w,g}=T$
. -
Consequence: We say that
 $\varphi $
is a consequence of
$\varphi $
is a consequence of
 $\Gamma $
— written
$\Gamma $
— written
 $\Gamma \models \varphi $
— iff for all
$\Gamma \models \varphi $
— iff for all
 $\mathcal {M},w,g$
, if
$\mathcal {M},w,g$
, if
 $ [[\gamma ]]^{\mathcal {M},w,g}=T$
for all
$ [[\gamma ]]^{\mathcal {M},w,g}=T$
for all
 $\gamma \in \Gamma $
, then
$\gamma \in \Gamma $
, then
 $ [[\varphi ]]^{\mathcal {M},w,g}=T$
.
$ [[\varphi ]]^{\mathcal {M},w,g}=T$
. -
Validity: We say that
 $\varphi $
is valid — written
$\varphi $
is valid — written
 $\models \varphi $
— iff
$\models \varphi $
— iff
 $\varnothing \models \varphi $
.
$\varnothing \models \varphi $
.
Definition 2.11 (Lambda hierarchy of falsities).
We make the following recursive definition of
![]() $\bot _{a}$
, for all
$\bot _{a}$
, for all
![]() $a\in \mathsf {KIND}_{t}$
:
$a\in \mathsf {KIND}_{t}$
:
-
•
 $\bot _t:=\bot $
.
$\bot _t:=\bot $
. -
•
 $\bot _{ab}:=\left \langle \lambda x_{a}\bot _{b}\right \rangle $
for all
$\bot _{ab}:=\left \langle \lambda x_{a}\bot _{b}\right \rangle $
for all
 $\langle a,b\rangle \in \mathsf {KIND}_{t}$
.
$\langle a,b\rangle \in \mathsf {KIND}_{t}$
.
Proposition 2.12. For all
![]() $c \in \mathsf {KIND}_t$
,
$c \in \mathsf {KIND}_t$
,
![]() $w\in W$
, and g an assignment on
$w\in W$
, and g an assignment on
![]() $\mathcal {M}$
we have that
$\mathcal {M}$
we have that
![]() $[[\bot _c]]^{\mathcal {M},w,g} = F_c$
.
$[[\bot _c]]^{\mathcal {M},w,g} = F_c$
.
Proof For type t we have
![]() $[[\bot ]]^{\mathcal {M},w,g}=F$
. So assume that
$[[\bot ]]^{\mathcal {M},w,g}=F$
. So assume that
![]() $[[\bot _{b}]]^{\mathcal {M},w,g}=F_{b}$
for an arbitrary
$[[\bot _{b}]]^{\mathcal {M},w,g}=F_{b}$
for an arbitrary
![]() $b\in \mathsf {KIND}_{t}$
. By definition,
$b\in \mathsf {KIND}_{t}$
. By definition,
![]() $[[\bot _{ab}]]^{\mathcal {M},w,g}=[[\left \langle \lambda x_{a}\bot _{b}\right \rangle ]]^{\mathcal {M},w,g}$
. Where:
$[[\bot _{ab}]]^{\mathcal {M},w,g}=[[\left \langle \lambda x_{a}\bot _{b}\right \rangle ]]^{\mathcal {M},w,g}$
. Where:

Thus,
![]() $[[\bot _{ab}]]^{\mathcal {M},w,g}=F_{ab}$
, and so
$[[\bot _{ab}]]^{\mathcal {M},w,g}=F_{ab}$
, and so
![]() $\bot _{c}$
names the constant function
$\bot _{c}$
names the constant function
![]() $F_{c}$
, for all
$F_{c}$
, for all
![]() $c \in \mathsf {KIND}_t$
.
$c \in \mathsf {KIND}_t$
.
3 Inspiration from Farmer’s work
Farmer [Reference Farmer10] distinguishes between kind e and kind t types; the first includes the type of individuals as well as the functions from elements of any type a to elements of kind e; the second includes the type of truth values as well as the type of functions from elements of any type a to elements of kind t.
Farmer’s goal was to develop a system based on Church’s theory of types but where partial functions could be reasoned about naturally, in accordance with standard mathematical practice. Our requirement was similar, but our point of departure was hybrid type theory with actualist quantification, and so we wanted local domains of quantification which varies all the way up in the type hierarchy.Footnote
2
We also want
![]() $\lambda $
-expressions to behave in a similar fashion to quantifiers: that is, the interpretation of a
$\lambda $
-expressions to behave in a similar fashion to quantifiers: that is, the interpretation of a
![]() $\lambda $
-expression in a world w should be a function whose arguments are local, and thus they should have the possibility of not returning a value for either non-denoting arguments or for outsiders (elements that are outside the local domain of quantification).
$\lambda $
-expression in a world w should be a function whose arguments are local, and thus they should have the possibility of not returning a value for either non-denoting arguments or for outsiders (elements that are outside the local domain of quantification).
The previous requirements of locality and partiality are appropriate for lambda expressions of kind e, but for lambda predicates and the formulas we create with them we wanted standard truth values in all worlds, and we agree with Farmer in sending to False formulas with non-denoting terms in a given world. In fact, a similar requirement applies for any
![]() $\lambda $
-expression of kind t and that is why we introduced (Definition 2.11) in the formal language of type theory the “lambda hierarchy of falsities” defining them recursively as either
$\lambda $
-expression of kind t and that is why we introduced (Definition 2.11) in the formal language of type theory the “lambda hierarchy of falsities” defining them recursively as either
![]() $\bot _{t}$
or the constant function
$\bot _{t}$
or the constant function
![]() $\bot _{ab}$
that sends every argument of type a to
$\bot _{ab}$
that sends every argument of type a to
![]() $\bot _{b}$
. The hierarchy of falsity functions introduced in Definition 2.3(4)(d) serves as interpretation of the “lambda hierarchy of falsities” as in any structure, F is the interpretation of
$\bot _{b}$
. The hierarchy of falsity functions introduced in Definition 2.3(4)(d) serves as interpretation of the “lambda hierarchy of falsities” as in any structure, F is the interpretation of
![]() $\bot _{t}$
and
$\bot _{t}$
and
![]() $F_{ab}$
the interpretation of
$F_{ab}$
the interpretation of
![]() $\bot _{ab}$
.
$\bot _{ab}$
.
Farmer analyses the major approaches for dealing with partial functions with quantifiers and arrives at the conclusion that he wants option “h) Partial evaluation for terms but total evaluation for formulas.” He also specified [Reference Farmer10, p. 1277] the five informal principles that motivate his semantics, and he added the following comments:
“Principles 1 and 2 say that expressions of kind e and kind t should be semantically different: expressions of kind e may be nondenoting but expressions of kind t must be denoting. Hence, the semantics allows for partial functions without sacrificing
![]() $2$
-valued logic. Principle 3 says that only applications may be nondenoting. Principle 4 states that nondenotation propagates up through expressions of kind e and that the application of an expression denoting a partial function to an expression denoting a value outside the function’s domain is itself nondenoting. Principle 5 says that the application of a predicate to a nondenoting expression is always false.”
$2$
-valued logic. Principle 3 says that only applications may be nondenoting. Principle 4 states that nondenotation propagates up through expressions of kind e and that the application of an expression denoting a partial function to an expression denoting a value outside the function’s domain is itself nondenoting. Principle 5 says that the application of a predicate to a nondenoting expression is always false.”
We modify some of his principles to deal with the fact that we are now modelling a modal logic and so our hierarchy is not only a partial type hierarchy able to distinguish kind e from kind t types, but also, inside the partial type hierarchy
![]() $\langle \mathsf {D}_{a}\rangle _{a\in \mathsf {TYPES }}$
we have local domains for each world all the way up in the hierarchy,
$\langle \mathsf {D}_{a}\rangle _{a\in \mathsf {TYPES }}$
we have local domains for each world all the way up in the hierarchy,
![]() $ \langle \mathsf {D}_{a}^{w}\rangle _{\langle w,a\rangle \in W\times \mathsf { TYPES}}$
. The distinction between kind e and kind t functions follows Farmer’s system; in the first case we take partial functions, while in the second the functions are total. For the local hierarchies, we decided that for kind e the local domain
$ \langle \mathsf {D}_{a}^{w}\rangle _{\langle w,a\rangle \in W\times \mathsf { TYPES}}$
. The distinction between kind e and kind t functions follows Farmer’s system; in the first case we take partial functions, while in the second the functions are total. For the local hierarchies, we decided that for kind e the local domain
![]() $\mathsf {D}_{ab}^{w}$
should include all the elements of
$\mathsf {D}_{ab}^{w}$
should include all the elements of
![]() $\mathsf {D}_{ab}$
whose functions return “undefined” for all the arguments that lies outside the local domain
$\mathsf {D}_{ab}$
whose functions return “undefined” for all the arguments that lies outside the local domain
![]() $\mathsf {D}_{a}^{w}$
; for kind t the local domain
$\mathsf {D}_{a}^{w}$
; for kind t the local domain
![]() $\mathsf {D} _{ab}^{w}$
should include all the elements of
$\mathsf {D} _{ab}^{w}$
should include all the elements of
![]() $\mathsf {D}_{ab}$
whose functions give the default value
$\mathsf {D}_{ab}$
whose functions give the default value
![]() $F_{b}$
for all the outsiders. We have also imposed some global constrains to the general interpretations, one is that we wanted that, at each level of the hierarchy, the domain
$F_{b}$
for all the outsiders. We have also imposed some global constrains to the general interpretations, one is that we wanted that, at each level of the hierarchy, the domain
![]() $\mathsf {D}_{a}$
be the union of all
$\mathsf {D}_{a}$
be the union of all
![]() $\mathsf {D}_{a}^{w}$
. Therefore, anything that denotes at world w has to reside (exist) in at least one local domain, say v. Therefore, for kind e denoting expressions of type
$\mathsf {D}_{a}^{w}$
. Therefore, anything that denotes at world w has to reside (exist) in at least one local domain, say v. Therefore, for kind e denoting expressions of type
![]() $\left \langle a,b\right \rangle $
the corresponding function, according to the interpretation at world w, residing at world v has to follow the local requirements for kind e functions at this world v; and a similar requirements hold for kind t expressions.
$\left \langle a,b\right \rangle $
the corresponding function, according to the interpretation at world w, residing at world v has to follow the local requirements for kind e functions at this world v; and a similar requirements hold for kind t expressions.
In our formal language, we will introduce formulas
![]() $\mathsf {EXISTS}(\alpha _{a})$
and
$\mathsf {EXISTS}(\alpha _{a})$
and
![]() $\mathsf {DEN}(\alpha _{a})$
expressing “
$\mathsf {DEN}(\alpha _{a})$
expressing “
![]() $\alpha _{a}$
exists” and “
$\alpha _{a}$
exists” and “
![]() $\alpha _{a}$
denotes” respectively (see Definition 5.1). When these formulas are evaluated at a world w we are able to distinguish between “being a member of the local domain
$\alpha _{a}$
denotes” respectively (see Definition 5.1). When these formulas are evaluated at a world w we are able to distinguish between “being a member of the local domain
![]() $\mathsf {D}_{a}^{w}$
” where the expression is being interpreted and “having a value in
$\mathsf {D}_{a}^{w}$
” where the expression is being interpreted and “having a value in
![]() $\mathsf {D}_{a}$
,” but maybe somewhere else, outside the local domain of interpretation,
$\mathsf {D}_{a}$
,” but maybe somewhere else, outside the local domain of interpretation,
![]() $\mathsf {D}_{a}^{w}$
. The last situation is expressed by
$\mathsf {D}_{a}^{w}$
. The last situation is expressed by
![]() $\overline {\mathsf {EXISTS}(\alpha _{a})}$
.
$\overline {\mathsf {EXISTS}(\alpha _{a})}$
.
Moreover, as well as the primitive equality,
![]() $\equiv $
(“strong” equality, which demands that both its arguments be defined) we define a binary equality relation,
$\equiv $
(“strong” equality, which demands that both its arguments be defined) we define a binary equality relation,
![]() $\simeq $
(“weak” equality) applied between expressions of the same type to express that either both denote the same in the world w or both lack denotation. Footnote
3
$\simeq $
(“weak” equality) applied between expressions of the same type to express that either both denote the same in the world w or both lack denotation. Footnote
3
These definitions play an important role in our calculus (Section 6.2) as some of the axioms (for example,
![]() $\forall $
-elimination, extensionality, or
$\forall $
-elimination, extensionality, or
![]() $\lambda $
-conversion) require the elements involved to exist. We also have some axioms requiring denotation or existence for a huge category of expressions, among them being the
$\lambda $
-conversion) require the elements involved to exist. We also have some axioms requiring denotation or existence for a huge category of expressions, among them being the
![]() $\lambda $
-existence axiom, which says that they all exist and, consequently, acts as a comprehension axiom. Finally, some of the functional schemas as well as the global constraints schemas involve existence, as we are stipulating how our existing functions should act on arguments.
$\lambda $
-existence axiom, which says that they all exist and, consequently, acts as a comprehension axiom. Finally, some of the functional schemas as well as the global constraints schemas involve existence, as we are stipulating how our existing functions should act on arguments.
4 Rigidity and substitution
In this section we discuss some fundamental syntactic concepts, and note some semantical results concerning them.
Notation 4.1 (Basic concepts).
Within an expression, a variable can be free or bound. A variable is free if it occurs in the expression and it is not in the scope of a lambda abstractor or quantifier. If a variable
![]() $x_{a}$
of type a is free in a meaningful expression
$x_{a}$
of type a is free in a meaningful expression
![]() $\alpha $
of any type, then it is bound in
$\alpha $
of any type, then it is bound in
![]() $\left \langle \lambda x_{a}\alpha \right \rangle $
. If a variable
$\left \langle \lambda x_{a}\alpha \right \rangle $
. If a variable
![]() $ x_{a}$
of type a is free in a formula
$ x_{a}$
of type a is free in a formula
![]() $\varphi $
, then it is bound in
$\varphi $
, then it is bound in
![]() $ \forall x_{a}\varphi $
. Similarly, if a state variable s is free in a meaningful expression
$ \forall x_{a}\varphi $
. Similarly, if a state variable s is free in a meaningful expression
![]() $\varphi $
of type t, then it is bound in
$\varphi $
of type t, then it is bound in
![]() ${ {\downarrow \hspace {-0.1 pt}} }s\varphi $
.Footnote
4
For any meaningful expression
${ {\downarrow \hspace {-0.1 pt}} }s\varphi $
.Footnote
4
For any meaningful expression
![]() $\alpha $
, the set of free variables that
$\alpha $
, the set of free variables that
![]() $\alpha $
contains is
$\alpha $
contains is
![]() $\mathsf {FREE}(\alpha )$
, and the set of free state variables that
$\mathsf {FREE}(\alpha )$
, and the set of free state variables that
![]() $\alpha $
contains is
$\alpha $
contains is
![]() $\mathsf {SFREE}(\alpha )$
. If
$\mathsf {SFREE}(\alpha )$
. If
![]() $\alpha $
contains neither free variables nor state variables (that is, if
$\alpha $
contains neither free variables nor state variables (that is, if
![]() $\mathsf {FREE} (\alpha )=\varnothing =\mathsf {SFREE}(\alpha )$
) then we say that
$\mathsf {FREE} (\alpha )=\varnothing =\mathsf {SFREE}(\alpha )$
) then we say that
![]() $\alpha $
is closed. Closed meaningful expressions play an important role in our completeness proof, and we write
$\alpha $
is closed. Closed meaningful expressions play an important role in our completeness proof, and we write
![]() $\mathsf {CME}_{a}$
for the set of closed meaningful expressions of type a. A closed meaningful expression of type t is called a sentence, so
$\mathsf {CME}_{a}$
for the set of closed meaningful expressions of type a. A closed meaningful expression of type t is called a sentence, so
![]() $\mathsf {CME}_{t}$
is the set of all sentences.
$\mathsf {CME}_{t}$
is the set of all sentences.
Lemma 4.2 (Coincidence Lemma for variables and state variables).
Let g and
![]() $g^{\ast }$
be assignments that agree on the values assigned to the free variables and state variables of
$g^{\ast }$
be assignments that agree on the values assigned to the free variables and state variables of
![]() $\alpha _{a}\in \mathsf {ME}_{a}$
and let
$\alpha _{a}\in \mathsf {ME}_{a}$
and let
![]() $\langle \mathcal {M},g\rangle $
and
$\langle \mathcal {M},g\rangle $
and
![]() $\langle \mathcal {M},g^{\ast }\rangle $
be general interpretations. Then for any world
$\langle \mathcal {M},g^{\ast }\rangle $
be general interpretations. Then for any world
![]() $w\in W$
we have that
$w\in W$
we have that
![]() $[[\alpha _{a}]]^{\mathcal {M},w,g}=[[\alpha _{a}]]^{\mathcal {M} ,w,g^{\ast }}$
(that is, either
$[[\alpha _{a}]]^{\mathcal {M},w,g}=[[\alpha _{a}]]^{\mathcal {M} ,w,g^{\ast }}$
(that is, either
![]() $\alpha _{a}$
denotes the same entity in
$\alpha _{a}$
denotes the same entity in
![]() $ \langle \mathcal {M},g\rangle $
and
$ \langle \mathcal {M},g\rangle $
and
![]() $\langle \mathcal {M},g^{\ast }\rangle $
, or they both are
$\langle \mathcal {M},g^{\ast }\rangle $
, or they both are
![]() $\divideontimes $
).
$\divideontimes $
).
Proof It is easy by induction on the construction of meaningful expressions.
Lemma 4.3 (Coincidence for nominals).
Let
![]() $\mathcal {M}=\langle \mathcal {S}, \mathsf {I}\rangle $
and
$\mathcal {M}=\langle \mathcal {S}, \mathsf {I}\rangle $
and
![]() $\mathcal {M^{\ast }}=\langle \mathcal {S},\mathsf {I} ^{\ast }\rangle $
be any two structures with the same skeleton such that
$\mathcal {M^{\ast }}=\langle \mathcal {S},\mathsf {I} ^{\ast }\rangle $
be any two structures with the same skeleton such that
![]() $ \mathsf {I}$
agrees with
$ \mathsf {I}$
agrees with
![]() $\mathsf {I}^{\ast }$
for all its arguments, the only possible exception being the value of nominal i. Let
$\mathsf {I}^{\ast }$
for all its arguments, the only possible exception being the value of nominal i. Let
![]() $\alpha _{a}\in \mathsf {ME}_{a}$
be any meaningful expression such that i does not occur in it. For any world w and assignment g,
$\alpha _{a}\in \mathsf {ME}_{a}$
be any meaningful expression such that i does not occur in it. For any world w and assignment g,
![]() $[[\alpha _{a}]]^{ \mathcal {M},w,g}=[[\alpha _{a}]]^{\mathcal {\ M}^{\ast },w,g}$
(that is, either
$[[\alpha _{a}]]^{ \mathcal {M},w,g}=[[\alpha _{a}]]^{\mathcal {\ M}^{\ast },w,g}$
(that is, either
![]() $\alpha _{a}$
denotes the same entity in
$\alpha _{a}$
denotes the same entity in
![]() $\langle \mathcal {M} ,g\rangle $
and
$\langle \mathcal {M} ,g\rangle $
and
![]() $\langle \mathcal {M},g^{\ast }\rangle $
, or they both are
$\langle \mathcal {M},g^{\ast }\rangle $
, or they both are
![]() $ \divideontimes $
).
$ \divideontimes $
).
Proof By induction on the construction of expressions where i does not occur.
4.1 Rigidity
The concept of rigidity is very important in modal logic: an expression is rigid if and only if it denotes the same entity in all worlds or does not denote in any world. We now syntactically define a set of meaningful expressions called
![]() $\mathsf {RIGIDS}$
, all of which are (semantically) rigid. These formulas play an important role in our completeness proof: our Henkin model will be built out of the closed elements in
$\mathsf {RIGIDS}$
, all of which are (semantically) rigid. These formulas play an important role in our completeness proof: our Henkin model will be built out of the closed elements in
![]() $\mathsf {RIGIDS}$
.
$\mathsf {RIGIDS}$
.
Definition 4.4. The set of
![]() $\mathsf {RIGIDS}$
is defined inductively as follows:
$\mathsf {RIGIDS}$
is defined inductively as follows:
where
![]() $h\in \mathsf {HYB}$
,
$h\in \mathsf {HYB}$
,
![]() $u_{a}\in \mathsf {VAR}$
,
$u_{a}\in \mathsf {VAR}$
,
![]() $c\in \mathsf {KIND }_{t}$
,
$c\in \mathsf {KIND }_{t}$
,
![]() $\delta _{a} \in \mathsf {ME}_{a}$
, and
$\delta _{a} \in \mathsf {ME}_{a}$
, and
![]() $\alpha _{a}$
,
$\alpha _{a}$
,
![]() $\gamma _{ba}$
,
$\gamma _{ba}$
,
![]() $\beta _{b}$
,
$\beta _{b}$
,
![]() $\mu _{a}$
,
$\mu _{a}$
,
![]() $ \varphi $
, and
$ \varphi $
, and
![]() $\psi $
are in
$\psi $
are in
![]() $\mathsf {RIGIDS}$
.
$\mathsf {RIGIDS}$
.
For each type a,
![]() $\mathsf {\ RIGIDS}_a$
denotes the set of rigid expressions of type a. We define
$\mathsf {\ RIGIDS}_a$
denotes the set of rigid expressions of type a. We define
![]() $\mathsf {RIGIDS}$
to be the set of all rigid expressions.
$\mathsf {RIGIDS}$
to be the set of all rigid expressions.
Lemma 4.5. Let
![]() $\langle \mathcal {M},g\rangle $
be a model, and
$\langle \mathcal {M},g\rangle $
be a model, and
![]() $ \gamma _{c}\in \mathsf {RIGIDS}$
. Then,
$ \gamma _{c}\in \mathsf {RIGIDS}$
. Then,
![]() $[[\gamma _{c}]]^{\mathcal {M} ,w,g}=[[\gamma _{c}]]^{\mathcal {M},v,g}$
for all worlds w, v on
$[[\gamma _{c}]]^{\mathcal {M} ,w,g}=[[\gamma _{c}]]^{\mathcal {M},v,g}$
for all worlds w, v on
![]() $\langle \mathcal {M},g\rangle $
(that is, either
$\langle \mathcal {M},g\rangle $
(that is, either
![]() $\gamma _{c}$
denotes the same at
$\gamma _{c}$
denotes the same at
![]() $w $
and v, or they both are
$w $
and v, or they both are
![]() $\divideontimes $
).
$\divideontimes $
).
Proof By induction on the construction of rigid expressions.
4.2 Substitution
Let
![]() $h\in \mathsf {HYB}$
. For all
$h\in \mathsf {HYB}$
. For all
![]() $\alpha _{a}\in \mathsf {ME}_{a}$
,
$\alpha _{a}\in \mathsf {ME}_{a}$
,
![]() $\alpha _{a}\frac {h}{s}$
is the meaningful expression obtained by the substitution of h for a state variable s in
$\alpha _{a}\frac {h}{s}$
is the meaningful expression obtained by the substitution of h for a state variable s in
![]() $ \alpha _{a}$
. Similarly, for all
$ \alpha _{a}$
. Similarly, for all
![]() $\alpha _{a}\in \mathsf {ME}_{a}$
,
$\alpha _{a}\in \mathsf {ME}_{a}$
,
![]() $ \alpha _{a}\frac {\gamma _{c}}{v_{c}}$
is the meaningful expression obtained by the substitution of
$ \alpha _{a}\frac {\gamma _{c}}{v_{c}}$
is the meaningful expression obtained by the substitution of
![]() $\gamma _{c}$
for a variable
$\gamma _{c}$
for a variable
![]() $v_{c}$
in
$v_{c}$
in
![]() $\alpha _{a}$
Footnote
5
. Here we just specify the definition of substitution for downarrow formulas:
$\alpha _{a}$
Footnote
5
. Here we just specify the definition of substitution for downarrow formulas:
 $$ \begin{align*} ({{\downarrow\hspace{-0.1 pt}} }s^{\prime }\varphi )\frac{h}{s}:=\left\{ \begin{array}{ll} {{\downarrow\hspace{-0.1 pt}} }s^{\prime }\varphi, & \text{if }s\not\in \mathsf{SFREE}({ {\downarrow\hspace{-0.1 pt}} }s^{\prime }\varphi ), \\ {{\downarrow\hspace{-0.1 pt}} }s^{\prime }(\varphi \frac{h}{s}), & \text{if }s\in \mathsf{ SFREE}({{\downarrow\hspace{-0.1 pt}} }s^{\prime }\varphi )\text{ and }h\not=s^{\prime }, \\ {{\downarrow\hspace{-0.1 pt}} }t(\varphi \frac{t}{s^{\prime }})\frac{h}{s}, &\begin{array}{c} \text{if }s\in \ \mathsf{SFREE}({{\downarrow\hspace{-0.1 pt}} }s^{\prime }\varphi )\text{ and }h=s^{\prime }, \\ \text{and }t\text{ is a new state variable}. \end{array} \end{array} \right. \end{align*} $$
$$ \begin{align*} ({{\downarrow\hspace{-0.1 pt}} }s^{\prime }\varphi )\frac{h}{s}:=\left\{ \begin{array}{ll} {{\downarrow\hspace{-0.1 pt}} }s^{\prime }\varphi, & \text{if }s\not\in \mathsf{SFREE}({ {\downarrow\hspace{-0.1 pt}} }s^{\prime }\varphi ), \\ {{\downarrow\hspace{-0.1 pt}} }s^{\prime }(\varphi \frac{h}{s}), & \text{if }s\in \mathsf{ SFREE}({{\downarrow\hspace{-0.1 pt}} }s^{\prime }\varphi )\text{ and }h\not=s^{\prime }, \\ {{\downarrow\hspace{-0.1 pt}} }t(\varphi \frac{t}{s^{\prime }})\frac{h}{s}, &\begin{array}{c} \text{if }s\in \ \mathsf{SFREE}({{\downarrow\hspace{-0.1 pt}} }s^{\prime }\varphi )\text{ and }h=s^{\prime }, \\ \text{and }t\text{ is a new state variable}. \end{array} \end{array} \right. \end{align*} $$
Lemma 4.6 (Nominal and state variable substitution).
Let
![]() $\langle \mathcal {M},g\rangle $
be a model and w a world in it. Then, for all
$\langle \mathcal {M},g\rangle $
be a model and w a world in it. Then, for all
![]() $\alpha _{a}\in \mathsf {ME}_{a}$
,
$\alpha _{a}\in \mathsf {ME}_{a}$
,
![]() $h\in \mathsf {HYB}$
and any state variable s:
$h\in \mathsf {HYB}$
and any state variable s:
where
![]() $g^{\ast }$
is an s-variant of g such that
$g^{\ast }$
is an s-variant of g such that
![]() $g^{\ast }(s)=v$
and either v is the unique world such that
$g^{\ast }(s)=v$
and either v is the unique world such that
![]() $[I(h)](v)=T$
, when
$[I(h)](v)=T$
, when
![]() $h\in \mathsf { NOM} $
or
$h\in \mathsf { NOM} $
or
![]() $g(h)=v$
, when
$g(h)=v$
, when
![]() $h\in \mathsf {SVAR}$
.
$h\in \mathsf {SVAR}$
.
Proof By induction on the construction of meaningful expressions, with the help of Lemma 4.2. Please, keep in mind the definition of substitution for downarrow formulas.
Rigid expressions that are defined behave well with respect to variable substitution:
Lemma 4.7 (Rigid substitution).
Let
![]() $\langle \mathcal {M},g\rangle $
be a model and w a world in it. Then, for all
$\langle \mathcal {M},g\rangle $
be a model and w a world in it. Then, for all
![]() $\alpha _{a}\in \mathsf {ME}_{a}$
, any variable
$\alpha _{a}\in \mathsf {ME}_{a}$
, any variable
![]() $v_{c}$
of type c and
$v_{c}$
of type c and
![]() $\gamma _{c}\in \mathsf {RIGIDS}_{c}$
such that
$\gamma _{c}\in \mathsf {RIGIDS}_{c}$
such that
![]() $[[\gamma _{c}]]^{\mathcal {M},w,g}$
is defined (
$[[\gamma _{c}]]^{\mathcal {M},w,g}$
is defined (
![]() $ \not =\divideontimes $
) we have
$ \not =\divideontimes $
) we have
 $$ \begin{align*} \left\lbrack \left\lbrack \alpha _{a}\frac{\gamma _{c}}{v_{c}}\right]\right]^{\mathcal{M} ,w,g}=[[\alpha _{a}]]^{\mathcal{M},w,g^{\ast }} \end{align*} $$
$$ \begin{align*} \left\lbrack \left\lbrack \alpha _{a}\frac{\gamma _{c}}{v_{c}}\right]\right]^{\mathcal{M} ,w,g}=[[\alpha _{a}]]^{\mathcal{M},w,g^{\ast }} \end{align*} $$
(either both denotes the same, or they both are
![]() $\divideontimes $
) where
$\divideontimes $
) where
![]() $ g^{\ast }$
is the
$ g^{\ast }$
is the
![]() $v_{c}$
-variant of g such that
$v_{c}$
-variant of g such that
![]() $g^{\ast }(v_{c})=[[\gamma _{c}]]^{\mathcal {M},w,g}$
.
$g^{\ast }(v_{c})=[[\gamma _{c}]]^{\mathcal {M},w,g}$
.
Proof By induction on the construction of meaningful expressions, with the help of Lemma 4.2.
Lemma 4.8. Let
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {M}^{\ast }$
be two almost equal structures, the only difference being the interpretation of a constant
$\mathcal {M}^{\ast }$
be two almost equal structures, the only difference being the interpretation of a constant
![]() $C_{b}$
. For any meaningful expression
$C_{b}$
. For any meaningful expression
![]() $\alpha _{a}$
where
$\alpha _{a}$
where
![]() $C_{b}$
does not occur,
$C_{b}$
does not occur,
for all
![]() $w\in W$
and assignment g.
$w\in W$
and assignment g.
Proof By induction on the construction of meaningful expressions.
5 Existence, denotation, equality, and falsities
In this section we illustrate the expressive power of
![]() $\mathcal {HPTT}$
by defining a number of key concepts which will play an important role in the article. In particular, we will introduce in the formal language the differences already mentioned between (1) denoting
$\mathcal {HPTT}$
by defining a number of key concepts which will play an important role in the article. In particular, we will introduce in the formal language the differences already mentioned between (1) denoting
![]() $\mathsf {DEN}(\alpha _{a})$
(having an interpretation in
$\mathsf {DEN}(\alpha _{a})$
(having an interpretation in
![]() $\mathsf {D}_{a}$
), (2) being an “outsider”
$\mathsf {D}_{a}$
), (2) being an “outsider”
![]() $\overline {\mathsf {EXISTS}(\alpha _{a})}$
(being a member of
$\overline {\mathsf {EXISTS}(\alpha _{a})}$
(being a member of
![]() $\mathsf {D}_{a}-\mathsf {D}_{a}^{w}$
) and, finally, (3) existing
$\mathsf {D}_{a}-\mathsf {D}_{a}^{w}$
) and, finally, (3) existing
![]() $\mathsf {EXISTS}(\alpha _{a})$
(being a member of the local domain
$\mathsf {EXISTS}(\alpha _{a})$
(being a member of the local domain
![]() $\mathsf {D}_{a}^{w}$
).
$\mathsf {D}_{a}^{w}$
).
Definition 5.1 (Denotation, existence, and equality).
For any expression
![]() $ \alpha _{a}$
of type a we define:
$ \alpha _{a}$
of type a we define:
-
•
 $\mathsf {EXISTS}(\alpha _{a}):=\left \langle \lambda x_{a}\top \right \rangle (\alpha _{a})$
, for
$\mathsf {EXISTS}(\alpha _{a}):=\left \langle \lambda x_{a}\top \right \rangle (\alpha _{a})$
, for
 $a\in \mathsf {TYPES}$
and
$a\in \mathsf {TYPES}$
and
 $a\not =t$
.
$a\not =t$
. -
•
 $\mathsf {EXISTS}(\varphi ):=(\varphi \equiv \top )\vee (\varphi \equiv \bot ).$
$\mathsf {EXISTS}(\varphi ):=(\varphi \equiv \top )\vee (\varphi \equiv \bot ).$
-
•
 $\mathsf {DEN}(\alpha _{a}):={{\downarrow \hspace {-0.1 pt}} }s(\mathsf {E}(\mathsf { EXISTS}{ (@}_{s}\alpha _{a})))$
, where
$\mathsf {DEN}(\alpha _{a}):={{\downarrow \hspace {-0.1 pt}} }s(\mathsf {E}(\mathsf { EXISTS}{ (@}_{s}\alpha _{a})))$
, where
 $s\not \in \mathsf {SFREE} (\alpha _{a})$
.
$s\not \in \mathsf {SFREE} (\alpha _{a})$
. -
•
 $\overline {\mathsf {EXISTS}(\alpha _{a})}:= \mathsf {DEN}(\alpha _{a}) \wedge \neg \mathsf {EXISTS}(\alpha _{a})$
.
$\overline {\mathsf {EXISTS}(\alpha _{a})}:= \mathsf {DEN}(\alpha _{a}) \wedge \neg \mathsf {EXISTS}(\alpha _{a})$
. -
•
 $\alpha _{a}\simeq \beta _{a}:=\mathsf {DEN}(\alpha _{a})\vee \mathsf {DEN}(\beta _{a})\rightarrow \alpha _{a}\equiv \beta _{a}$
, for any
$\alpha _{a}\simeq \beta _{a}:=\mathsf {DEN}(\alpha _{a})\vee \mathsf {DEN}(\beta _{a})\rightarrow \alpha _{a}\equiv \beta _{a}$
, for any
 $a\in \mathsf {TYPE}$
, where
$a\in \mathsf {TYPE}$
, where
 $s\not \in \mathsf {SFREE}(\alpha _{a})\cup \mathsf {SFREE}(\beta _{a})$
. (Here s is the state variable bounded by down arrow in both
$s\not \in \mathsf {SFREE}(\alpha _{a})\cup \mathsf {SFREE}(\beta _{a})$
. (Here s is the state variable bounded by down arrow in both
 $\mathsf {DEN}(\alpha _{a}) $
and
$\mathsf {DEN}(\alpha _{a}) $
and
 $ \mathsf {DEN}(\beta _{a})$
.)
$ \mathsf {DEN}(\beta _{a})$
.)
Remark 5.2. When we interpret these formulas:
-
• Formula
 $\mathsf {EXISTS}{\small (}\alpha _{a})$
means that the interpretation of the expression
$\mathsf {EXISTS}{\small (}\alpha _{a})$
means that the interpretation of the expression
 $\alpha _{a}$
in
$\alpha _{a}$
in
 $\langle \mathcal {M} ,g\rangle $
at the world w is not only defined (
$\langle \mathcal {M} ,g\rangle $
at the world w is not only defined (
 $\not =\divideontimes $
) but also it belongs to the local domain of type a; i.e,
$\not =\divideontimes $
) but also it belongs to the local domain of type a; i.e,
 $[[\mathsf { EXISTS}{\small (}\alpha _{a})]]^{\mathcal {M},w,g}=T$
iff
$[[\mathsf { EXISTS}{\small (}\alpha _{a})]]^{\mathcal {M},w,g}=T$
iff
 $[[\alpha _{a}]]^{\mathcal {M},w,g}\in \mathsf {D}_{a}^{w}$
Footnote
6
.
$[[\alpha _{a}]]^{\mathcal {M},w,g}\in \mathsf {D}_{a}^{w}$
Footnote
6
. -
• However,
 $\mathsf {DEN}(\alpha _{a})$
says something different, namely that if an expression
$\mathsf {DEN}(\alpha _{a})$
says something different, namely that if an expression
 $\alpha _{a}$
is defined (
$\alpha _{a}$
is defined (
 $\not =\divideontimes $
) when we evaluate it at some world w (the world that
$\not =\divideontimes $
) when we evaluate it at some world w (the world that
 ${\downarrow }$
labels as s) then the entity
${\downarrow }$
labels as s) then the entity
 $[[\alpha _{a}]]^{\mathcal {M},w,g}$
exists at some world (the
$[[\alpha _{a}]]^{\mathcal {M},w,g}$
exists at some world (the
 $\mathsf {E}$
modality lets us see this world).
$\mathsf {E}$
modality lets us see this world). -
• In case we wanted
 $\mathsf {DEN}(\alpha _{a})$
to be applied only to rigid expressions the definition could be simplified as
$\mathsf {DEN}(\alpha _{a})$
to be applied only to rigid expressions the definition could be simplified as
 $\mathsf {DEN }(\alpha _{a}):=\mathsf {E}(\mathsf {EXISTS}{\small (}\alpha _{a}))$
.
$\mathsf {DEN }(\alpha _{a}):=\mathsf {E}(\mathsf {EXISTS}{\small (}\alpha _{a}))$
. -
• With these definitions, it is easy to see that
 $\models \mathsf {EXIST} (\alpha _{a})\rightarrow \mathsf {DEN}(\alpha _{a})$
and also that
$\models \mathsf {EXIST} (\alpha _{a})\rightarrow \mathsf {DEN}(\alpha _{a})$
and also that
 $\models \mathsf {DEN}(\alpha _{a}) \equiv \mathsf {EXISTS}(\alpha _{a}) \lor \overline {\mathsf {EXISTS}(\alpha _{a})}$
.
$\models \mathsf {DEN}(\alpha _{a}) \equiv \mathsf {EXISTS}(\alpha _{a}) \lor \overline {\mathsf {EXISTS}(\alpha _{a})}$
. -
• The formula
 $\alpha _{a}\simeq \beta _{a}$
means that either the expressions
$\alpha _{a}\simeq \beta _{a}$
means that either the expressions
 $\alpha _{a}$
and
$\alpha _{a}$
and
 $\beta _{a}$
denote the same object in the world w under the interpretation
$\beta _{a}$
denote the same object in the world w under the interpretation
 $\langle \mathcal {M},g\rangle $
or both lack denotation, i.e.,
$\langle \mathcal {M},g\rangle $
or both lack denotation, i.e.,
 $[[\alpha _{a}\simeq \beta _{a}]]^{\mathcal {M},w,g}=T$
iff either
$[[\alpha _{a}\simeq \beta _{a}]]^{\mathcal {M},w,g}=T$
iff either
 $[[\lnot \mathsf {DEN}(\alpha _{a})]]^{\mathcal {M} ,w,g}=T=[[\lnot \mathsf {DEN}(\beta _{a})]]^{\mathcal {M},w,g}$
or
$[[\lnot \mathsf {DEN}(\alpha _{a})]]^{\mathcal {M} ,w,g}=T=[[\lnot \mathsf {DEN}(\beta _{a})]]^{\mathcal {M},w,g}$
or
 $ [[\alpha _{a}\equiv \beta _{a}]]^{\mathcal {M},w,g}=T$
(both are defined and equal,
$ [[\alpha _{a}\equiv \beta _{a}]]^{\mathcal {M},w,g}=T$
(both are defined and equal,
 $[[\alpha _{a}]]^{\mathcal {M},w,g}=[[\beta _{a}]]^{\mathcal {M},w,g}$
). To put it another way,
$[[\alpha _{a}]]^{\mathcal {M},w,g}=[[\beta _{a}]]^{\mathcal {M},w,g}$
). To put it another way,
 $\alpha _{a}\simeq \beta _{a}$
corresponds in the object language to the way we use ordinary set-theoretic equality.
$\alpha _{a}\simeq \beta _{a}$
corresponds in the object language to the way we use ordinary set-theoretic equality. -
• The difference between formulas
 $\alpha _{a}\simeq \beta _{a}$
and
$\alpha _{a}\simeq \beta _{a}$
and
 $ \alpha _{a}\equiv \beta _{a}$
is shown at the table, where we put
$ \alpha _{a}\equiv \beta _{a}$
is shown at the table, where we put
 $[[\alpha _{a}]]^{\mathcal {M},w,g}=\divideontimes $
instead of
$[[\alpha _{a}]]^{\mathcal {M},w,g}=\divideontimes $
instead of
 $[[\mathsf {DEN}(\alpha _{a})]]^{\mathcal {M},w,g}=F$
and
$[[\mathsf {DEN}(\alpha _{a})]]^{\mathcal {M},w,g}=F$
and
 $[[\alpha _{a}]]^{\mathcal {M} ,w,g}\not =\divideontimes $
instead of
$[[\alpha _{a}]]^{\mathcal {M} ,w,g}\not =\divideontimes $
instead of
 $[[\mathsf {DEN}(\alpha _{a})]]^{ \mathcal {M},w,g}=T$
. We define
$[[\mathsf {DEN}(\alpha _{a})]]^{ \mathcal {M},w,g}=T$
. We define
 $A=[[\alpha _{a}]]^{\mathcal {M},w,g}$
and
$A=[[\alpha _{a}]]^{\mathcal {M},w,g}$
and
 $B=[[\beta _{a}]]^{ \mathcal {M},w,g}$
in the table in Figure 1.
$B=[[\beta _{a}]]^{ \mathcal {M},w,g}$
in the table in Figure 1.

Figure 1 Strong versus weak equality.
6 Axiomatizing
 $\mathcal {HPTT}$
$\mathcal {HPTT}$
We now axiomatize
![]() $\mathcal {HPTT}$
. We first discuss the rules of proof, then the axioms, note a number of theorems
$\mathcal {HPTT}$
. We first discuss the rules of proof, then the axioms, note a number of theorems
![]() $\mathcal {HPTT}$
that will be useful in subsequent sections, and then prove the soundness of two of the more complex axiom schemas.
$\mathcal {HPTT}$
that will be useful in subsequent sections, and then prove the soundness of two of the more complex axiom schemas.
6.1 Rules of proof
We use the following standard rules of proof. We remind the reader that we use h as metavariable over elements of
![]() $\mathsf { HYB}$
(that is, h is either a nominal or a state variable) and that
$\mathsf { HYB}$
(that is, h is either a nominal or a state variable) and that
![]() $ \mathsf {EXISTS}(c_{a}):=\langle \lambda x_{a}\top \rangle (c_{a})$
.
$ \mathsf {EXISTS}(c_{a}):=\langle \lambda x_{a}\top \rangle (c_{a})$
.
-
(1) Modus Ponens: If
 $\vdash \varphi $
and
$\vdash \varphi $
and
 $\vdash \varphi \rightarrow \psi $
, then
$\vdash \varphi \rightarrow \psi $
, then
 $\vdash \psi $
.
$\vdash \psi $
. -
(2) Generalization:
-
(a) Gen
 $_{\Box }$
: If
$_{\Box }$
: If
 $\vdash \varphi $
, then
$\vdash \varphi $
, then
 $\vdash \Box \varphi $
.
$\vdash \Box \varphi $
. -
(b) Gen
 $_{\mathsf {A}}$
: If
$_{\mathsf {A}}$
: If
 $\vdash \varphi $
, then
$\vdash \varphi $
, then
 $\vdash \mathsf {A}\varphi $
.
$\vdash \mathsf {A}\varphi $
. -
(c) Gen
 $_{\mathsf {@}}$
: If
$_{\mathsf {@}}$
: If
 $\vdash \varphi $
, then
$\vdash \varphi $
, then
 $\vdash @_h\varphi $
.
$\vdash @_h\varphi $
. -
(d) Gen
 $_{\forall }$
: If
$_{\forall }$
: If
 $\vdash \varphi $
, then
$\vdash \varphi $
, then
 $\vdash \forall x_a\varphi $
.
$\vdash \forall x_a\varphi $
.
-
-
(3) Name: If
 $\vdash h\rightarrow \varphi $
, and h does not occur in
$\vdash h\rightarrow \varphi $
, and h does not occur in
 $\varphi $
, then
$\varphi $
, then
 $\vdash \varphi $
.
$\vdash \varphi $
. -
(4) Paste: If j is a nominal different from i (
 $j\not =i$
) and
$j\not =i$
) and
 $c_{a}$
is a constant, not occurring in
$c_{a}$
is a constant, not occurring in
 $\varphi $
,
$\varphi $
,
 $\psi $
or
$\psi $
or
 $\theta $
:
$\theta $
:-
(a) Paste
 $_{\Diamond }$
: If
$_{\Diamond }$
: If
 $\vdash @_{i}\Diamond j\wedge @_{j}\varphi \rightarrow \theta $
, then
$\vdash @_{i}\Diamond j\wedge @_{j}\varphi \rightarrow \theta $
, then
 $\vdash @_{i}\Diamond \varphi \rightarrow \theta $
.
$\vdash @_{i}\Diamond \varphi \rightarrow \theta $
. -
(b) Paste
 $_{\exists }$
: If
$_{\exists }$
: If
 $\vdash @_{i}(\mathsf {EXISTS}(c_{a}))\wedge @_{i}\varphi \frac {@_{i}c_{a}}{x_{a}}\rightarrow \psi $
, then
$\vdash @_{i}(\mathsf {EXISTS}(c_{a}))\wedge @_{i}\varphi \frac {@_{i}c_{a}}{x_{a}}\rightarrow \psi $
, then
 $\vdash @_{i}\exists x_{a}\varphi \rightarrow \psi $
.
$\vdash @_{i}\exists x_{a}\varphi \rightarrow \psi $
. -
(c) Paste
 $_{\mathsf {E}}$
: If
$_{\mathsf {E}}$
: If
 $\vdash @_{i}\mathsf {E}j\wedge @_{j}\varphi \rightarrow \theta $
, then
$\vdash @_{i}\mathsf {E}j\wedge @_{j}\varphi \rightarrow \theta $
, then
 $\vdash @_{i}\mathsf {E}\varphi \rightarrow \theta $
.
$\vdash @_{i}\mathsf {E}\varphi \rightarrow \theta $
.
-
As the Name and Paste rules will play such an important role in our Lindenbaum construction, the following remarks may be helpful. The Name rule can be read as (something like) a natural deduction rule saying:
If
![]() $\varphi $
can be proved to hold at an arbitrary world named h that is not mentioned in
$\varphi $
can be proved to hold at an arbitrary world named h that is not mentioned in
![]() $\varphi $
, then we can (so to speak) discharge the h and prove
$\varphi $
, then we can (so to speak) discharge the h and prove
![]() $\varphi $
.
$\varphi $
.
The Paste
![]() $_{\Diamond }$
, Paste
$_{\Diamond }$
, Paste
![]() $_{\exists }$
, and Paste
$_{\exists }$
, and Paste
![]() $_{\mathsf {E}}$
rules are best thought of as (something like) sequent or tableax rules. For example, we can read Paste
$_{\mathsf {E}}$
rules are best thought of as (something like) sequent or tableax rules. For example, we can read Paste
![]() $_{\Diamond }$
from bottom to top as follows: To prove
$_{\Diamond }$
from bottom to top as follows: To prove
![]() $\theta $
from
$\theta $
from
![]() $@_i\Diamond \varphi $
, introduce a new nominal j, and try to prove
$@_i\Diamond \varphi $
, introduce a new nominal j, and try to prove
![]() $\theta $
from
$\theta $
from
![]() $@_i\Diamond j$
and
$@_i\Diamond j$
and
![]() $@_j\varphi $
instead.
$@_j\varphi $
instead.
The significance of the Name and Paste rules will become clear in Section 8 when they will be used to license the introduction of Henkin-style witness nominals and rigidified constants in the Lindenbaum construction. For more on these rules, see [Reference Blackburn and ten Cate8].
6.2 Axioms
Before stating the axioms, a general remark. Many of our axioms state properties of our defined symbols
![]() $\mathsf {EXISTS(\alpha )}$
,
$\mathsf {EXISTS(\alpha )}$
,
![]() $\mathsf {DEN}(\alpha )$
, and
$\mathsf {DEN}(\alpha )$
, and
![]() $\alpha \simeq \beta $
, or relate them in various way; see Definition 5.1 for their definitions, and recall that we always use them in a way that prevents the accidental binding of state variables. Also, two of our axioms (
$\alpha \simeq \beta $
, or relate them in various way; see Definition 5.1 for their definitions, and recall that we always use them in a way that prevents the accidental binding of state variables. Also, two of our axioms (
![]() $\forall $
-elimination and
$\forall $
-elimination and
![]() $ \lambda $
-conversion) make use of rigid substitution; recall that our Substitution Lemma 4.7 is proven for rigids and denoting expressions. Bearing this in mind, as axioms we take all
$ \lambda $
-conversion) make use of rigid substitution; recall that our Substitution Lemma 4.7 is proven for rigids and denoting expressions. Bearing this in mind, as axioms we take all
![]() $\mathcal {HPTT}$
instances of propositional tautologies together with all
$\mathcal {HPTT}$
instances of propositional tautologies together with all
![]() $\mathcal {HPTT}$
instances of the following schemas:
$\mathcal {HPTT}$
instances of the following schemas:
-
(1) Distributivity schemas:
-
(a)
 $\Box $
-distributivity:
$\Box $
-distributivity:
 $\vdash \square (\varphi \rightarrow \psi )\rightarrow (\square \varphi \rightarrow \square \psi )$
.
$\vdash \square (\varphi \rightarrow \psi )\rightarrow (\square \varphi \rightarrow \square \psi )$
. -
(b)
 $\mathsf {A}$
-distributivity:
$\mathsf {A}$
-distributivity:
 $\vdash \mathsf {A}(\varphi \rightarrow \psi )\rightarrow (\mathsf {A}\varphi \rightarrow \mathsf {A}\psi )$
.
$\vdash \mathsf {A}(\varphi \rightarrow \psi )\rightarrow (\mathsf {A}\varphi \rightarrow \mathsf {A}\psi )$
. -
(c)
 $@$
-distributivity:
$@$
-distributivity:
 $\vdash @_{h}(\varphi \rightarrow \psi )\rightarrow (@_{h}\varphi \rightarrow @_{h}\psi )$
.
$\vdash @_{h}(\varphi \rightarrow \psi )\rightarrow (@_{h}\varphi \rightarrow @_{h}\psi )$
. -
(d)
 $\forall $
-distributivity:
$\forall $
-distributivity:
 $\vdash \forall x_a(\varphi \rightarrow \psi )\rightarrow (\forall x_a\varphi \rightarrow \forall x_a\psi )$
.
$\vdash \forall x_a(\varphi \rightarrow \psi )\rightarrow (\forall x_a\varphi \rightarrow \forall x_a\psi )$
.
-
-
(2) Quantifier schemas:
-
(a) Individuals-exist:
 $\exists x_e\top $
.
$\exists x_e\top $
. -
(b)
 $\forall $
-elimination:
$\forall $
-elimination:
 $\vdash \forall x_a\varphi \rightarrow (\mathsf {EXISTS}(\alpha _a)\rightarrow \varphi (\frac {\alpha _a}{x_a}))$
, if
$\vdash \forall x_a\varphi \rightarrow (\mathsf {EXISTS}(\alpha _a)\rightarrow \varphi (\frac {\alpha _a}{x_a}))$
, if
 $\alpha _a\in \mathsf {RIGIDS}$
.
$\alpha _a\in \mathsf {RIGIDS}$
. -
(c) Vacuous:
 $\vdash \varphi \rightarrow \forall x_a\varphi $
, where
$\vdash \varphi \rightarrow \forall x_a\varphi $
, where
 $x_a$
does not occur free in
$x_a$
does not occur free in
 $ \varphi $
.
$ \varphi $
.
-
-
(3) Basic hybrid schemas:
-
(a) Ref:
 $\vdash @_{h}h$
.
$\vdash @_{h}h$
. -
(b) Selfdual:
 $\vdash @_{h}\varphi \equiv \lnot @_{h}\lnot \varphi $
.
$\vdash @_{h}\varphi \equiv \lnot @_{h}\lnot \varphi $
. -
(c) Intro:
 $\vdash h\rightarrow (\alpha _a\simeq @_{h}\alpha _a)$
.
$\vdash h\rightarrow (\alpha _a\simeq @_{h}\alpha _a)$
. -
(d) Rigids are rigid:
 $\vdash @_{h}\alpha _{a}\simeq \alpha _{a}$
, if
$\vdash @_{h}\alpha _{a}\simeq \alpha _{a}$
, if
 $\alpha _{a}\in \mathsf {RIGIDS}$
(as a special case we have the common Agree Axiom:
$\alpha _{a}\in \mathsf {RIGIDS}$
(as a special case we have the common Agree Axiom:
 $\vdash @_{h^{\prime }}@_{h}\alpha _{a}\simeq @_{h}\alpha _{a}$
).
$\vdash @_{h^{\prime }}@_{h}\alpha _{a}\simeq @_{h}\alpha _{a}$
).
-
-
(4) Equality schemas:
-
(a) Reflexivity:
 $\vdash \alpha _{a}\simeq \alpha _{a}$
.
$\vdash \alpha _{a}\simeq \alpha _{a}$
. -
(b) Symmetry:
 $\vdash \alpha _{a}\simeq \beta _{a}\rightarrow \beta _{a}\simeq \alpha _{a}$
.
$\vdash \alpha _{a}\simeq \beta _{a}\rightarrow \beta _{a}\simeq \alpha _{a}$
. -
(c) Transitivity:
 $\vdash \alpha _{a}\simeq \beta _{a}\wedge \beta _{a}\simeq \delta _{a}\rightarrow \alpha _{a}\simeq \delta _{a}$
.
$\vdash \alpha _{a}\simeq \beta _{a}\wedge \beta _{a}\simeq \delta _{a}\rightarrow \alpha _{a}\simeq \delta _{a}$
.
-
-
(5) Interaction with
 $@$
schemas:
$@$
schemas:-
(a) Equality-at-named-worlds:
 $\vdash @_{h}(\beta _{b}\equiv \delta _{b})\equiv (@_{h}\beta _{b}\equiv @_{h}\delta _{b})$
.
$\vdash @_{h}(\beta _{b}\equiv \delta _{b})\equiv (@_{h}\beta _{b}\equiv @_{h}\delta _{b})$
. -
(b) Rigid function application:
 $ \vdash @_{h}(\gamma _{ab}\alpha _{a})\simeq @_{h}(\gamma _{ab})(@_{h}\alpha _{a})$
.
$ \vdash @_{h}(\gamma _{ab}\alpha _{a})\simeq @_{h}(\gamma _{ab})(@_{h}\alpha _{a})$
.
-
-
(6) Universal modality schemas:
-
(a) Universal relation definition:
 $\vdash \mathsf {E}h$
.
$\vdash \mathsf {E}h$
. -
(b) Interplay
 $@$
-
$@$
-
 $\mathsf {E}$
:
$\mathsf {E}$
:
 $\vdash @_{i}\mathsf {E}\varphi \equiv \mathsf {E}\varphi $
.
$\vdash @_{i}\mathsf {E}\varphi \equiv \mathsf {E}\varphi $
.
-
-
(7) DA schema:
 $\vdash @_{i}({{\downarrow \hspace {-0.1 pt}} } s\varphi \equiv \varphi (\frac {i}{s}))$
.
$\vdash @_{i}({{\downarrow \hspace {-0.1 pt}} } s\varphi \equiv \varphi (\frac {i}{s}))$
. -
(8) Denotation axioms:
-
(a)
 $\vdash \mathsf {DEN}(x_{a})$
.
$\vdash \mathsf {DEN}(x_{a})$
. -
(b)
 $\vdash \mathsf {DEN}(\alpha _{a})$
, with
$\vdash \mathsf {DEN}(\alpha _{a})$
, with
 $a\in \mathsf {KIND}_{t}$
.
$a\in \mathsf {KIND}_{t}$
. -
(c)
 $\vdash \mathsf {E(DEN}(c_{a}))$
, with
$\vdash \mathsf {E(DEN}(c_{a}))$
, with
 $c_{a}\in \mathsf {CON}_{a}$
.
$c_{a}\in \mathsf {CON}_{a}$
. -
(d)
 $\vdash \mathsf {DEN}(\gamma _{ab}\alpha _{a})\rightarrow (\mathsf {DEN}(\gamma _{ab})\wedge \mathsf {DEN}(\alpha _{a}))$
, with
$\vdash \mathsf {DEN}(\gamma _{ab}\alpha _{a})\rightarrow (\mathsf {DEN}(\gamma _{ab})\wedge \mathsf {DEN}(\alpha _{a}))$
, with
 $ \langle a,b\rangle \in \mathsf {KIND}_{e}$
.
$ \langle a,b\rangle \in \mathsf {KIND}_{e}$
. -
(e)
 $\vdash \alpha _{a}\equiv \beta _{a}\rightarrow \mathsf {DEN}(\alpha _{a}) \wedge \mathsf {DEN}(\beta _{a})$
.
$\vdash \alpha _{a}\equiv \beta _{a}\rightarrow \mathsf {DEN}(\alpha _{a}) \wedge \mathsf {DEN}(\beta _{a})$
. -
(f)
 $\vdash \lnot (\gamma _{ab}\alpha _{a}\equiv \bot _{b})\rightarrow \mathsf {DEN}(\alpha _{a})$
, with
$\vdash \lnot (\gamma _{ab}\alpha _{a}\equiv \bot _{b})\rightarrow \mathsf {DEN}(\alpha _{a})$
, with
 $ \langle a,b\rangle \in \mathsf {KIND}_{t}$
.
$ \langle a,b\rangle \in \mathsf {KIND}_{t}$
.
-
-
(9) Existence axioms:
-
(a)
 $\vdash \mathsf {EXISTS}(\left \langle \lambda x_{a}\beta _{b}\right \rangle )$
.
$\vdash \mathsf {EXISTS}(\left \langle \lambda x_{a}\beta _{b}\right \rangle )$
. -
(b)
 $\vdash \mathsf {EXISTS}(\alpha _{a})\rightarrow \mathsf {DEN}(\alpha _{a})$
.
$\vdash \mathsf {EXISTS}(\alpha _{a})\rightarrow \mathsf {DEN}(\alpha _{a})$
.
-
-
(10)
 $\lambda $
-conversion:
$\lambda $
-conversion:
 $\vdash \mathsf {EXISTS}(\alpha _{a})\rightarrow \left \langle \lambda x_{a}\beta _{b}\right \rangle (\alpha _{a})\simeq \beta _{b}\frac {\alpha _{a} }{x_{a}}\text {, where }\alpha _{a}\in \mathsf {RIGIDS}$
.
$\vdash \mathsf {EXISTS}(\alpha _{a})\rightarrow \left \langle \lambda x_{a}\beta _{b}\right \rangle (\alpha _{a})\simeq \beta _{b}\frac {\alpha _{a} }{x_{a}}\text {, where }\alpha _{a}\in \mathsf {RIGIDS}$
. -
(11) Functional schemas:
-
(a)
 $\vdash \alpha _{a}\simeq \beta _{a}\rightarrow \gamma _{ab}\alpha _{a}\simeq \gamma _{ab}\beta _{a}$
.
$\vdash \alpha _{a}\simeq \beta _{a}\rightarrow \gamma _{ab}\alpha _{a}\simeq \gamma _{ab}\beta _{a}$
. -
(b)
 $\vdash \gamma _{ab}\simeq \delta _{ab}\rightarrow \gamma _{ab}\alpha _{a}\simeq \delta _{ab}\alpha _{a}$
.
$\vdash \gamma _{ab}\simeq \delta _{ab}\rightarrow \gamma _{ab}\alpha _{a}\simeq \delta _{ab}\alpha _{a}$
. -
(c)
 $\vdash (\mathsf {EXISTS}{\small (}\gamma _{ab})\wedge \mathsf {DEN}(\gamma _{ab}\alpha _{a}))\rightarrow \mathsf {EXISTS}(\alpha _{a})$
, for
$\vdash (\mathsf {EXISTS}{\small (}\gamma _{ab})\wedge \mathsf {DEN}(\gamma _{ab}\alpha _{a}))\rightarrow \mathsf {EXISTS}(\alpha _{a})$
, for
 $\langle a,b\rangle \in \mathsf { KIND}_{e}$
.
$\langle a,b\rangle \in \mathsf { KIND}_{e}$
. -
(d)
 $\vdash (\mathsf {EXISTS}(\gamma _{a,b})\wedge \lnot (\gamma _{ab}\alpha _{a}\equiv \bot _{b}))\rightarrow \mathsf {\ EXISTS}(\alpha _{a})$
, with
$\vdash (\mathsf {EXISTS}(\gamma _{a,b})\wedge \lnot (\gamma _{ab}\alpha _{a}\equiv \bot _{b}))\rightarrow \mathsf {\ EXISTS}(\alpha _{a})$
, with
 $\langle a,b\rangle \in \mathsf {KIND}_{t}$
.
$\langle a,b\rangle \in \mathsf {KIND}_{t}$
.
-
-
(12) Extensionality schema:
 $\vdash (\mathsf {EXISTS}(\gamma _{ab})\wedge \mathsf {EXISTS}(\delta _{ab}))\rightarrow (\forall x_{a}\left ( \gamma _{ab}x_{a}\simeq \delta _{ab}x_{a}\right ) \equiv (\gamma _{ab}\equiv \delta _{ab}))$
, where
$\vdash (\mathsf {EXISTS}(\gamma _{ab})\wedge \mathsf {EXISTS}(\delta _{ab}))\rightarrow (\forall x_{a}\left ( \gamma _{ab}x_{a}\simeq \delta _{ab}x_{a}\right ) \equiv (\gamma _{ab}\equiv \delta _{ab}))$
, where
 $x_{a}\not \in \mathsf {FREE}(\gamma _{ab})\cup \mathsf {FREE}(\delta _{ab})$
.
$x_{a}\not \in \mathsf {FREE}(\gamma _{ab})\cup \mathsf {FREE}(\delta _{ab})$
. -
(13) Global constraints schemas:
-
(a)
 $\vdash \mathsf {DEN}(\gamma _{ab})\rightarrow (@_{i}(\mathsf {EXISTS}(\gamma _{ab}))\equiv \mathsf {A}(\lnot i\rightarrow \forall x_{a}(\lnot @_{i}(\mathsf {EXISTS}(x_{a}))\rightarrow \lnot \mathsf {DEN}(\gamma _{ab}x_{a}))))$
, with
$\vdash \mathsf {DEN}(\gamma _{ab})\rightarrow (@_{i}(\mathsf {EXISTS}(\gamma _{ab}))\equiv \mathsf {A}(\lnot i\rightarrow \forall x_{a}(\lnot @_{i}(\mathsf {EXISTS}(x_{a}))\rightarrow \lnot \mathsf {DEN}(\gamma _{ab}x_{a}))))$
, with
 $\gamma _{ab}\in \mathsf {CME}_{ab}\cap \mathsf {RIGIDS}$
,
$\gamma _{ab}\in \mathsf {CME}_{ab}\cap \mathsf {RIGIDS}$
,
 $\langle a,b\rangle \in \mathsf {KIND}_{e}$
.
$\langle a,b\rangle \in \mathsf {KIND}_{e}$
. -
(b)
 $\vdash @_{i}(\mathsf {EXISTS}(\gamma _{ab}))\equiv \mathsf {A}(\lnot i\rightarrow \forall x_{a}(\lnot @_{i}( \mathsf {EXISTS}(x_{a}))\rightarrow \gamma _{ab}x_{a}\equiv \bot _{b})))$
, with
$\vdash @_{i}(\mathsf {EXISTS}(\gamma _{ab}))\equiv \mathsf {A}(\lnot i\rightarrow \forall x_{a}(\lnot @_{i}( \mathsf {EXISTS}(x_{a}))\rightarrow \gamma _{ab}x_{a}\equiv \bot _{b})))$
, with
 $\gamma _{ab}\in \mathsf {CME}_{ab}\cap \mathsf {RIGIDS}$
,
$\gamma _{ab}\in \mathsf {CME}_{ab}\cap \mathsf {RIGIDS}$
,
 $\langle a,b\rangle \in \mathsf {KIND}_{t}$
.
$\langle a,b\rangle \in \mathsf {KIND}_{t}$
.
-
Definition 6.1 (Proofs)
As usual, we shall say that a proof of a formula
![]() $\varphi $
is a finite sequence of formulas ending with
$\varphi $
is a finite sequence of formulas ending with
![]() $\varphi $
such that every formula in the sequence is either an axiom, or it is obtained from previous formula(s) in the sequence using the rules of proof. We write
$\varphi $
such that every formula in the sequence is either an axiom, or it is obtained from previous formula(s) in the sequence using the rules of proof. We write
![]() $\vdash \varphi $
whenever we have such a sequence and say that
$\vdash \varphi $
whenever we have such a sequence and say that
![]() $\varphi $
is a
$\varphi $
is a
![]() $\mathcal {HPTT}$
-theorem.
$\mathcal {HPTT}$
-theorem.
If
![]() $\Gamma \cup \{\varphi \}$
is a set of meaningful expressions of type t, a proof of
$\Gamma \cup \{\varphi \}$
is a set of meaningful expressions of type t, a proof of
![]() $\varphi $
from
$\varphi $
from
![]() $\Gamma $
is a proof of
$\Gamma $
is a proof of
![]() $\vdash \gamma _{1}\wedge \cdots \wedge \gamma _{n}\rightarrow \varphi $
where
$\vdash \gamma _{1}\wedge \cdots \wedge \gamma _{n}\rightarrow \varphi $
where
![]() $\{\gamma _{1},\ldots ,\gamma _{n}\}\subseteq \Gamma $
. A meaningful expression
$\{\gamma _{1},\ldots ,\gamma _{n}\}\subseteq \Gamma $
. A meaningful expression
![]() $ \varphi $
of type t is provable from a set of expressions
$ \varphi $
of type t is provable from a set of expressions
![]() $\Gamma $
(written
$\Gamma $
(written
![]() $\Gamma \vdash \varphi $
) if and only if there is a proof of
$\Gamma \vdash \varphi $
) if and only if there is a proof of
![]() $ \varphi $
from
$ \varphi $
from
![]() $\Gamma $
. We call
$\Gamma $
. We call
![]() $\Gamma $
inconsistent if and only if for all formulas
$\Gamma $
inconsistent if and only if for all formulas
![]() $\varphi $
,
$\varphi $
,
![]() $\Gamma \vdash \varphi $
. Otherwise
$\Gamma \vdash \varphi $
. Otherwise
![]() $\Gamma $
is consistent.
$\Gamma $
is consistent.
Remark. Due to the definition of
![]() $\Gamma \vdash \varphi $
, it is easy to see that the deduction theorem holds.
$\Gamma \vdash \varphi $
, it is easy to see that the deduction theorem holds.
6.3 Some theorems of
 $\mathcal {HPTT}$
$\mathcal {HPTT}$
Two well-known derivable schemas of propositional hybrid logic will play a role in our completeness proof, namely the Bridge
![]() $_{\Diamond }$
schema
$_{\Diamond }$
schema
![]() $@_{i}\Diamond j\wedge @_{j}\varphi \rightarrow @_{i}\Diamond \varphi $
and the Back
$@_{i}\Diamond j\wedge @_{j}\varphi \rightarrow @_{i}\Diamond \varphi $
and the Back
![]() $_{\Diamond }$
schema
$_{\Diamond }$
schema
![]() $\Diamond @_{i}\varphi \rightarrow @_{i}\varphi $
. Both are provable in
$\Diamond @_{i}\varphi \rightarrow @_{i}\varphi $
. Both are provable in
![]() $\mathcal {HPTT} $
, and indeed, so are their counterparts containing the universal modality, namely the Bridge
$\mathcal {HPTT} $
, and indeed, so are their counterparts containing the universal modality, namely the Bridge
![]() $_{\mathsf {E}}$
schema
$_{\mathsf {E}}$
schema
![]() $@_{i}\mathsf {E}j\wedge @_{j}\varphi \rightarrow @_{i}\mathsf {E}\varphi $
and the Back
$@_{i}\mathsf {E}j\wedge @_{j}\varphi \rightarrow @_{i}\mathsf {E}\varphi $
and the Back
![]() $_{ \mathsf {E}}$
schema
$_{ \mathsf {E}}$
schema
![]() $\mathsf {E}@_{i}\varphi \rightarrow @_{i}\varphi $
. See [Reference Blackburn and ten Cate8] for the derivations.
$\mathsf {E}@_{i}\varphi \rightarrow @_{i}\varphi $
. See [Reference Blackburn and ten Cate8] for the derivations.
Furthermore, the following rule Name
![]() $^{\prime }$
is derivable: If
$^{\prime }$
is derivable: If
![]() $ \vdash @_{i} \varphi $
(with
$ \vdash @_{i} \varphi $
(with
![]() $i \in \mathsf {NOM}$
does not occur in
$i \in \mathsf {NOM}$
does not occur in
![]() $\varphi $
), then
$\varphi $
), then
![]() $\vdash \varphi $
. Starting from
$\vdash \varphi $
. Starting from
![]() $\vdash @_{i} \varphi $
,
$\vdash @_{i} \varphi $
,
![]() $\vdash \varphi $
is obtained by Proposition 26(2a), classical tautologies, Modus Ponens, and Name (Rule (3)).
$\vdash \varphi $
is obtained by Proposition 26(2a), classical tautologies, Modus Ponens, and Name (Rule (3)).
Proposition 6.2. The following are all theorems of
![]() $\mathcal {HPTT}$
.Footnote
7
$\mathcal {HPTT}$
.Footnote
7
-
(1)
 $\vdash @_{i}\varphi \rightarrow \mathsf {E} \varphi $
.
$\vdash @_{i}\varphi \rightarrow \mathsf {E} \varphi $
. -
(2)
 $\vdash @_{i}(\varphi \rightarrow \psi )\equiv (@_{i}\varphi \rightarrow @_{i}\psi )$
.
$\vdash @_{i}(\varphi \rightarrow \psi )\equiv (@_{i}\varphi \rightarrow @_{i}\psi )$
. -
(3)
 $\vdash \varphi \rightarrow \mathsf {E}\varphi $
.
$\vdash \varphi \rightarrow \mathsf {E}\varphi $
. -
(4)
 $\vdash \mathsf {E}\varphi \rightarrow \mathsf {A}\mathsf {E} \varphi $
.
$\vdash \mathsf {E}\varphi \rightarrow \mathsf {A}\mathsf {E} \varphi $
. -
(5)
 $\vdash \varphi \rightarrow \mathsf {A}\mathsf {E}\varphi $
.
$\vdash \varphi \rightarrow \mathsf {A}\mathsf {E}\varphi $
. -
(6)
 $\vdash \Diamond \varphi \rightarrow \mathsf {E} \varphi $
.
$\vdash \Diamond \varphi \rightarrow \mathsf {E} \varphi $
. -
(7)
 $\vdash \mathsf {E}h\equiv @_{h^{\prime }} \mathsf {E}h$
.
$\vdash \mathsf {E}h\equiv @_{h^{\prime }} \mathsf {E}h$
.
The proofs are in Appendix 12.1.
Of more relevance for the present paper, however, are the theorems stated in the following proposition.
Proposition 6.3. We next list some theorems which play an important role in the completeness proof.
-
(1) Denotes and equality. The first theorem states the equivalence between two possible definitions of denotation. The second one is a significant result, because it states that both “equalities” are the same for expressions which denote.
-
(a)
 $\vdash \mathsf {DEN}(\alpha _{a})\equiv (\alpha _{a} \equiv \alpha _{a})$
.
$\vdash \mathsf {DEN}(\alpha _{a})\equiv (\alpha _{a} \equiv \alpha _{a})$
. -
(b)
 $\vdash \mathsf {DEN}(\alpha )\rightarrow ((\alpha \simeq \beta )\equiv (\alpha \equiv \beta ))$
.
$\vdash \mathsf {DEN}(\alpha )\rightarrow ((\alpha \simeq \beta )\equiv (\alpha \equiv \beta ))$
.A consequence is that for kind t expressions
 $\vdash (\alpha \simeq \beta )\equiv (\alpha \equiv \beta )$
, because, by Axiom 8b, all kind t expressions denote. Hence, we will often write
$\vdash (\alpha \simeq \beta )\equiv (\alpha \equiv \beta )$
, because, by Axiom 8b, all kind t expressions denote. Hence, we will often write
 $\alpha \equiv \beta $
instead of
$\alpha \equiv \beta $
instead of
 $\alpha \simeq \beta $
for kind t expressions.
$\alpha \simeq \beta $
for kind t expressions. -
(c)
 $\vdash \mathsf {DEN}(@_{h}\alpha _{a})\equiv @_{h}\mathsf {DEN}(\alpha _{a})$
.
$\vdash \mathsf {DEN}(@_{h}\alpha _{a})\equiv @_{h}\mathsf {DEN}(\alpha _{a})$
. -
(d)
 $\vdash (\mathsf {DEN}(\alpha _{a})\wedge \alpha _{a}\simeq \beta _{a})\rightarrow \mathsf {DEN}(\beta _{a})$
.
$\vdash (\mathsf {DEN}(\alpha _{a})\wedge \alpha _{a}\simeq \beta _{a})\rightarrow \mathsf {DEN}(\beta _{a})$
. -
(e)
 $\mathsf {DEN}$
for rigids:
$\mathsf {DEN}$
for rigids:
 $\vdash \mathsf {DEN }(\alpha _{a})\equiv \mathsf {DEN}(@_{i}\alpha _{a})$
,
$\vdash \mathsf {DEN }(\alpha _{a})\equiv \mathsf {DEN}(@_{i}\alpha _{a})$
,
 $\alpha _{a}\in \mathsf {RIGIDS}$
as well as
$\alpha _{a}\in \mathsf {RIGIDS}$
as well as
 $\vdash \mathsf {DEN}(\alpha _{a})\equiv @_{i}\mathsf {DEN}(\alpha _{a})$
.
$\vdash \mathsf {DEN}(\alpha _{a})\equiv @_{i}\mathsf {DEN}(\alpha _{a})$
. -
(f)
 $\vdash \mathsf {DEN(}@_{h}(\gamma _{ab}\alpha _{a}))\rightarrow @_{h}(\gamma _{ab}\alpha _{a})\equiv (@_{h}\gamma _{ab}\alpha _{a}))$
, for
$\vdash \mathsf {DEN(}@_{h}(\gamma _{ab}\alpha _{a}))\rightarrow @_{h}(\gamma _{ab}\alpha _{a})\equiv (@_{h}\gamma _{ab}\alpha _{a}))$
, for
 $\alpha _{a}\in \mathsf {RIGIDS}$
.
$\alpha _{a}\in \mathsf {RIGIDS}$
.
-
-
(2) Weak equality versus strong equality in axioms. The formulas listed here are a rewriting of the corresponding axioms and their proofs depend on the fact that expressions of kind t always denote (Axiom 8b) along with the previous theorem (1b). In the first place, some Basic Hybrid Schemas can be expressed with strong equality instead of weak. For the same reason, some Functional Schemas also have a formulation with strong equality. And the same applies for
 $\lambda $
-conversion Axiom.
$\lambda $
-conversion Axiom.-
(a) Intro:
 $\vdash h\rightarrow (\alpha _{a}\equiv @_{h}\alpha _{a})$
, with
$\vdash h\rightarrow (\alpha _{a}\equiv @_{h}\alpha _{a})$
, with
 $a\in \mathsf {KIND}_{t}$
.
$a\in \mathsf {KIND}_{t}$
. -
(b) Rigids are rigid:
 $ \vdash @_{h^{\prime }}@_{h}\alpha _{a}\equiv @_{h}\alpha _{a}$
,
$ \vdash @_{h^{\prime }}@_{h}\alpha _{a}\equiv @_{h}\alpha _{a}$
,
 $a\in \mathsf {KIND}_{t}$
. (As a special case we have the common Agree Axiom
$a\in \mathsf {KIND}_{t}$
. (As a special case we have the common Agree Axiom
 $\vdash @_{i}\alpha _{a}\equiv \alpha _{a}$
,
$\vdash @_{i}\alpha _{a}\equiv \alpha _{a}$
,
 $\alpha _{a}\in \mathsf {RIGIDS}$
,
$\alpha _{a}\in \mathsf {RIGIDS}$
,
 $a\in \mathsf {KIND}_{t}$
.)
$a\in \mathsf {KIND}_{t}$
.) -
(c) Weak equal arguments:
 $\vdash \alpha _{a}\simeq \beta _{a}\rightarrow \gamma _{ab}\alpha _{a}\equiv \gamma _{ab}\beta _{a}$
, for
$\vdash \alpha _{a}\simeq \beta _{a}\rightarrow \gamma _{ab}\alpha _{a}\equiv \gamma _{ab}\beta _{a}$
, for
 $\langle a,b\rangle \in \mathsf {KIND}_{t}$
. (As a particular case, when arguments also denote,
$\langle a,b\rangle \in \mathsf {KIND}_{t}$
. (As a particular case, when arguments also denote,
 $\vdash \mathsf {DEN(}\alpha _{a})\rightarrow (\alpha _{a}\equiv \beta _{a}\rightarrow (\gamma _{ab}\alpha _{a}\equiv \gamma _{ab}\alpha _{a}))$
, for
$\vdash \mathsf {DEN(}\alpha _{a})\rightarrow (\alpha _{a}\equiv \beta _{a}\rightarrow (\gamma _{ab}\alpha _{a}\equiv \gamma _{ab}\alpha _{a}))$
, for
 $\langle a,b\rangle \in \mathsf {KIND}_{t}$
.)
$\langle a,b\rangle \in \mathsf {KIND}_{t}$
.) -
(d) Strong equal functions:
 $\vdash \gamma _{ab}\equiv \delta _{ab}\rightarrow (\gamma _{ab}\alpha _{a}\equiv \delta _{ab}\alpha _{a})$
, where
$\vdash \gamma _{ab}\equiv \delta _{ab}\rightarrow (\gamma _{ab}\alpha _{a}\equiv \delta _{ab}\alpha _{a})$
, where
 $\langle a,b\rangle \in \mathsf {KIND}_{t}$
.
$\langle a,b\rangle \in \mathsf {KIND}_{t}$
. -
(e) Strong
 $\lambda $
-conversion:
$\lambda $
-conversion:
 $\vdash \mathsf {EXISTS}(\alpha _{a})\rightarrow (\left \langle \lambda x_{a}\beta _{b}\right \rangle \alpha _{a}\equiv \beta _{b}\frac {\alpha _{a}}{x_{a}})$
, where
$\vdash \mathsf {EXISTS}(\alpha _{a})\rightarrow (\left \langle \lambda x_{a}\beta _{b}\right \rangle \alpha _{a}\equiv \beta _{b}\frac {\alpha _{a}}{x_{a}})$
, where
 $\alpha _{a}\in \mathsf {RIGIDS}$
and
$\alpha _{a}\in \mathsf {RIGIDS}$
and
 $ b\in \mathsf {KIND}_{t}$
.
$ b\in \mathsf {KIND}_{t}$
. -
(f)
 $\vdash @_{h}(\beta _{b}\simeq \delta _{b})\equiv (@_{h}\beta _{b}\simeq @_{h}\delta _{b})$
.
$\vdash @_{h}(\beta _{b}\simeq \delta _{b})\equiv (@_{h}\beta _{b}\simeq @_{h}\delta _{b})$
.
-
-
(3) Denotes versus exists. We will see that, in case our definition of
 $\mathsf {DEN}$
is used for rigids, we can employ an equivalent formulation (both semantically and sintactically) without downarrow.
$\mathsf {DEN}$
is used for rigids, we can employ an equivalent formulation (both semantically and sintactically) without downarrow.-
(a) New
 $\mathsf {DEN}$
definition for rigids:
$\mathsf {DEN}$
definition for rigids:
 $\vdash \mathsf {DEN}(\alpha _{a})\equiv \mathsf {E(EXIST}(\alpha _{a}))$
, with
$\vdash \mathsf {DEN}(\alpha _{a})\equiv \mathsf {E(EXIST}(\alpha _{a}))$
, with
 $\alpha _{a}\in \mathsf {RIGIDS}$
.
$\alpha _{a}\in \mathsf {RIGIDS}$
. -
(b)
 $\mathsf {EXISTS}$
implies common Exists definition:
$\mathsf {EXISTS}$
implies common Exists definition:
 $\vdash \mathsf {EXISTS}(\alpha _{a})\rightarrow \exists x_{a}(x_{a}\equiv \alpha _{a})$
, where
$\vdash \mathsf {EXISTS}(\alpha _{a})\rightarrow \exists x_{a}(x_{a}\equiv \alpha _{a})$
, where
 $\alpha _{a}\in \mathsf {RIGIDS }$
, as a particular case of the introduction of existential quantifier
$\alpha _{a}\in \mathsf {RIGIDS }$
, as a particular case of the introduction of existential quantifier
 $\vdash ( \mathsf {EXISTS}(\alpha _{a})\wedge \varphi \frac {\alpha _{a}}{x_{a}} )\rightarrow \exists x_{a}\varphi $
, where
$\vdash ( \mathsf {EXISTS}(\alpha _{a})\wedge \varphi \frac {\alpha _{a}}{x_{a}} )\rightarrow \exists x_{a}\varphi $
, where
 $\alpha _{a}\in \mathsf {RIGIDS}$
.
$\alpha _{a}\in \mathsf {RIGIDS}$
.
-
The proof is in Appendix 12.2.
Theorem 6.4 (Soundness).
For all
![]() $\varphi \in \mathsf {ME}_t$
, we have
$\varphi \in \mathsf {ME}_t$
, we have
![]() $\vdash \varphi $
implies
$\vdash \varphi $
implies
![]() $\models \varphi $
.
$\models \varphi $
.
Proof We will only prove the soundness of two of our more complex schemas, namely the Global constraints schemas (13a and 13b), because the proof is easy for the rest of the elements of the calculus.
-
• Global constraints schema for kind e.
 $\mathsf {DEN}(\gamma _{ab})\rightarrow (@_{i}(\mathsf {EXISTS}(\gamma _{ab}))\equiv \mathsf {A}(\lnot i\rightarrow \forall x_{a}(\lnot @_{i}(\mathsf { EXISTS}(x_{a}))\rightarrow \lnot \mathsf {DEN}(\gamma _{ab}x_{a}))))$
,
$\mathsf {DEN}(\gamma _{ab})\rightarrow (@_{i}(\mathsf {EXISTS}(\gamma _{ab}))\equiv \mathsf {A}(\lnot i\rightarrow \forall x_{a}(\lnot @_{i}(\mathsf { EXISTS}(x_{a}))\rightarrow \lnot \mathsf {DEN}(\gamma _{ab}x_{a}))))$
,where
 $\gamma _{ab}\in \mathsf {CME}_{ab}\cap \mathsf {RIGIDS} $
,
$\gamma _{ab}\in \mathsf {CME}_{ab}\cap \mathsf {RIGIDS} $
,
 $\langle a,b\rangle \in \mathsf {TYPES}_{e}$
.
$\langle a,b\rangle \in \mathsf {TYPES}_{e}$
.Let
 $\left \langle \mathcal {M},g\right \rangle $
be any general interpretation and
$\left \langle \mathcal {M},g\right \rangle $
be any general interpretation and
 $w\in W$
an arbitrary world. To see that the Global constraints schema is true under this interpretation at that world we assume that
$w\in W$
an arbitrary world. To see that the Global constraints schema is true under this interpretation at that world we assume that
 $\lbrack \lbrack \mathsf {DEN}(\gamma _{ab})]]^{\mathcal {M},w,g}=T$
, and so
$\lbrack \lbrack \mathsf {DEN}(\gamma _{ab})]]^{\mathcal {M},w,g}=T$
, and so
 $[[\gamma _{ab}]]^{\mathcal {M},w,g}\not =\divideontimes $
.We divide the proof of the biconditional
$[[\gamma _{ab}]]^{\mathcal {M},w,g}\not =\divideontimes $
.We divide the proof of the biconditional
 $\lbrack \lbrack @_{i}(\mathsf {EXISTS}(\gamma _{ab}))\equiv \mathsf {A}(\lnot i\rightarrow \forall x_{a}(\lnot @_{i}(\mathsf {EXISTS}(x_{a}))\rightarrow \lnot \mathsf {DEN}(\gamma _{ab}x_{a}))]]^{\mathcal {M},w,g}=T$
into two conditional parts. By definition:
$\lbrack \lbrack @_{i}(\mathsf {EXISTS}(\gamma _{ab}))\equiv \mathsf {A}(\lnot i\rightarrow \forall x_{a}(\lnot @_{i}(\mathsf {EXISTS}(x_{a}))\rightarrow \lnot \mathsf {DEN}(\gamma _{ab}x_{a}))]]^{\mathcal {M},w,g}=T$
into two conditional parts. By definition:-
–
 $[[@_{i}(\mathsf {EXISTS}(\gamma _{ab}))]]^{\mathcal {M},w,g}{\kern-1.2pt}={\kern-1.2pt}T$
iff
$[[@_{i}(\mathsf {EXISTS}(\gamma _{ab}))]]^{\mathcal {M},w,g}{\kern-1.2pt}={\kern-1.2pt}T$
iff
 $[[\gamma _{ab}]]^{\mathcal {M},v,g}{\kern-1.2pt}\in{\kern-1.2pt} \mathsf {\ D}_{ab}^{v}$
, with
$[[\gamma _{ab}]]^{\mathcal {M},v,g}{\kern-1.2pt}\in{\kern-1.2pt} \mathsf {\ D}_{ab}^{v}$
, with
 $\left [ \mathsf {I}(i)\right ] (v){\kern-1.2pt}={\kern-1.2pt}T$
.
$\left [ \mathsf {I}(i)\right ] (v){\kern-1.2pt}={\kern-1.2pt}T$
. -
–
 $[[\mathsf {A}(\lnot i\rightarrow \forall x_{a}(\lnot @_{i} \mathsf {\ EXISTS}(x_{a}))\rightarrow \lnot \mathsf {DEN}(\gamma _{ab}x_{a}))]]^{\mathcal {\ M},w,g}=T$
iff for all
$[[\mathsf {A}(\lnot i\rightarrow \forall x_{a}(\lnot @_{i} \mathsf {\ EXISTS}(x_{a}))\rightarrow \lnot \mathsf {DEN}(\gamma _{ab}x_{a}))]]^{\mathcal {\ M},w,g}=T$
iff for all
 $u\in W$
,
$u\in W$
,
 $\left [ \mathsf {I }(i)\right ] (u)=T$
or
$\left [ \mathsf {I }(i)\right ] (u)=T$
or
 $\ [[\forall x_{a}(\lnot @_{i}(\mathsf {EXISTS} (x_{a}))\rightarrow \lnot \mathsf {\ DEN}(\gamma _{ab}x_{a}))]]^{\mathcal {M} ,u,g}=T$
.
$\ [[\forall x_{a}(\lnot @_{i}(\mathsf {EXISTS} (x_{a}))\rightarrow \lnot \mathsf {\ DEN}(\gamma _{ab}x_{a}))]]^{\mathcal {M} ,u,g}=T$
.
 $(\Rightarrow )$
Let
$(\Rightarrow )$
Let
 $[[@_{i}(\mathsf {EXISTS}(\gamma _{ab}))]]^{\mathcal {M} ,w,g}=T$
. So we know that
$[[@_{i}(\mathsf {EXISTS}(\gamma _{ab}))]]^{\mathcal {M} ,w,g}=T$
. So we know that
 $[[\gamma _{ab}]]^{\mathcal {M},v,g}$
, as any member of
$[[\gamma _{ab}]]^{\mathcal {M},v,g}$
, as any member of
 $\mathsf {D}_{ab}^{v}$
, must satisfy the locality for kind e condition and returns undefined
$\mathsf {D}_{ab}^{v}$
, must satisfy the locality for kind e condition and returns undefined
 $[[\gamma _{ab}]]^{\mathcal {M} ,v,g}(\theta )=\divideontimes $
for any
$[[\gamma _{ab}]]^{\mathcal {M} ,v,g}(\theta )=\divideontimes $
for any
 $\theta \in \mathsf {D}_{a}-\mathsf {D} _{a}^{v}$
.
$\theta \in \mathsf {D}_{a}-\mathsf {D} _{a}^{v}$
.To be true at w the universal modality formula, it has to be true at any
 $ u\in W$
. In case
$ u\in W$
. In case
 $\left [ \mathsf {I}(i)\right ] (u)=T$
the proof is done. Suppose that
$\left [ \mathsf {I}(i)\right ] (u)=T$
the proof is done. Suppose that
 $\left [ \mathsf {I}(i)\right ] (u)=F$
. To prove that the generalization formula is true at u, take any
$\left [ \mathsf {I}(i)\right ] (u)=F$
. To prove that the generalization formula is true at u, take any
 $\theta \in \mathsf {D} _{a}^{u}$
and assume, in order to arrive to a contradiction, that
$\theta \in \mathsf {D} _{a}^{u}$
and assume, in order to arrive to a contradiction, that
 $\lbrack \lbrack \lnot @_{i}\mathsf {EXISTS}(x_{a})]]^{\mathcal {M} ,u,g_{x_{a}}^{\theta }}=T$
but
$\lbrack \lbrack \lnot @_{i}\mathsf {EXISTS}(x_{a})]]^{\mathcal {M} ,u,g_{x_{a}}^{\theta }}=T$
but
 $\lbrack \lbrack \mathsf {DEN}(\gamma _{ab}x_{a})]]^{\mathcal {M} ,u,g_{x_{a}}^{\theta }}=T$
. From the first assumption we get that
$\lbrack \lbrack \mathsf {DEN}(\gamma _{ab}x_{a})]]^{\mathcal {M} ,u,g_{x_{a}}^{\theta }}=T$
. From the first assumption we get that
 $\theta \not \in \mathsf {D}_{a}^{v}$
. From the second, we get that there is a world
$\theta \not \in \mathsf {D}_{a}^{v}$
. From the second, we get that there is a world
 $w^{\ast }$
where
$w^{\ast }$
where
 $[[\gamma _{ab}]]^{\mathcal {M} ,u,\left ( g_{x_{a}}^{\theta }\right ) _{s}^{u}}(\theta )\in \mathsf {D} _{b}^{w^{\ast }}$
and so
$[[\gamma _{ab}]]^{\mathcal {M} ,u,\left ( g_{x_{a}}^{\theta }\right ) _{s}^{u}}(\theta )\in \mathsf {D} _{b}^{w^{\ast }}$
and so
 $[[\gamma _{ab}]]^{\mathcal {M},u,\left ( g_{x_{a}}^{\theta }\right ) _{s}^{u}}(\theta )\not =\divideontimes $
. However,
$[[\gamma _{ab}]]^{\mathcal {M},u,\left ( g_{x_{a}}^{\theta }\right ) _{s}^{u}}(\theta )\not =\divideontimes $
. However,
 $\gamma _{ab}\in \mathsf {CME}_{\langle a,b\rangle }\cap \mathsf {RIGIDS}$
and so
$\gamma _{ab}\in \mathsf {CME}_{\langle a,b\rangle }\cap \mathsf {RIGIDS}$
and so
 $[[\gamma _{ab}]]^{\mathcal {M} ,u,\left ( g_{x_{a}}^{\theta }\right ) _{s}^{u}}=[[\gamma _{ab}]]^{\mathcal {M} ,v,g}$
. Being equal functions, the value of
$[[\gamma _{ab}]]^{\mathcal {M} ,u,\left ( g_{x_{a}}^{\theta }\right ) _{s}^{u}}=[[\gamma _{ab}]]^{\mathcal {M} ,v,g}$
. Being equal functions, the value of
 $\theta $
must be the same, but
$\theta $
must be the same, but
 $ [[\gamma _{ab}]]^{\mathcal {M},v,g}(\theta )=\divideontimes $
(due to the locality for kind e condition) while
$ [[\gamma _{ab}]]^{\mathcal {M},v,g}(\theta )=\divideontimes $
(due to the locality for kind e condition) while
 $[[\gamma _{ab}]]^{\mathcal {M},u,\left ( g_{x_{a}}^{\theta }\right ) _{s}^{u}}(\theta )\not =\divideontimes $
. This is a contradiction. Therefore,
$[[\gamma _{ab}]]^{\mathcal {M},u,\left ( g_{x_{a}}^{\theta }\right ) _{s}^{u}}(\theta )\not =\divideontimes $
. This is a contradiction. Therefore,
 $[[\lnot \mathsf { DEN}(\gamma _{ab}x_{a})]]^{\mathcal {M},u,g_{x_{a}}^{\theta }}=T$
.
$[[\lnot \mathsf { DEN}(\gamma _{ab}x_{a})]]^{\mathcal {M},u,g_{x_{a}}^{\theta }}=T$
. $(\Leftarrow )$
Suppose that the universal modality formula is true at w. We want to prove that
$(\Leftarrow )$
Suppose that the universal modality formula is true at w. We want to prove that
 $[[@_{i}(\mathsf {EXISTS}(\gamma _{ab}))]]^{\mathcal {M} ,w,g}=T$
. To obtain a contradiction suppose the opposite, that
$[[@_{i}(\mathsf {EXISTS}(\gamma _{ab}))]]^{\mathcal {M} ,w,g}=T$
. To obtain a contradiction suppose the opposite, that
 $[[\gamma _{ab}]]^{ \mathcal {M},v,g}\not \in \mathsf {D}_{ab}^{v}$
, with
$[[\gamma _{ab}]]^{ \mathcal {M},v,g}\not \in \mathsf {D}_{ab}^{v}$
, with
 $\left [ \mathsf {I}(i) \right ] (v)=T$
. By definition of local domains, the last condition means: (a)
$\left [ \mathsf {I}(i) \right ] (v)=T$
. By definition of local domains, the last condition means: (a)
 $Def([[\gamma _{ab}]]^{\mathcal {M},v,g})\not \subseteq \mathsf {D}_{a}^{v}$
or (b)
$Def([[\gamma _{ab}]]^{\mathcal {M},v,g})\not \subseteq \mathsf {D}_{a}^{v}$
or (b)
 $[[\gamma _{ab}]]^{\mathcal {M},v,g}=\divideontimes $
.
$[[\gamma _{ab}]]^{\mathcal {M},v,g}=\divideontimes $
.Case
 $(a)$
: If
$(a)$
: If
 $Def([[\gamma _{ab}]]^{\mathcal {M},v,g})\not \subseteq \mathsf {D} _{a}^{v}$
, there is some
$Def([[\gamma _{ab}]]^{\mathcal {M},v,g})\not \subseteq \mathsf {D} _{a}^{v}$
, there is some
 $\theta \in \mathsf {D}_{a}-\mathsf {D}_{a}^{v}$
such that
$\theta \in \mathsf {D}_{a}-\mathsf {D}_{a}^{v}$
such that
 $[[\gamma _{ab}]]^{\mathcal {M},v,g}(\theta )\neq \divideontimes $
and so
$[[\gamma _{ab}]]^{\mathcal {M},v,g}(\theta )\neq \divideontimes $
and so
 $[[\mathsf {DEN}(\gamma _{ab}x_{a})]]^{\mathcal {M},v,g_{x_{a}}^{\theta }}=T $
.
$[[\mathsf {DEN}(\gamma _{ab}x_{a})]]^{\mathcal {M},v,g_{x_{a}}^{\theta }}=T $
.Let
 $u\in W$
with
$u\in W$
with
 $\left [ \mathsf {I}(i)\right ] (u)=F$
and so: if
$\left [ \mathsf {I}(i)\right ] (u)=F$
and so: if
 $[[\lnot @_{i}(\mathsf {EXISTS}(x_{a}))]]^{\mathcal {M},u,g_{x_{a}}^{\theta }}=T$
then
$[[\lnot @_{i}(\mathsf {EXISTS}(x_{a}))]]^{\mathcal {M},u,g_{x_{a}}^{\theta }}=T$
then
 $ [[\lnot \mathsf {DEN}(\gamma _{ab}x_{a})]]^{\mathcal {M},u,g_{x_{a}}^{\theta }}=T$
. As
$ [[\lnot \mathsf {DEN}(\gamma _{ab}x_{a})]]^{\mathcal {M},u,g_{x_{a}}^{\theta }}=T$
. As
 $\theta \not \in \mathsf {D}_{a}^{v}$
,
$\theta \not \in \mathsf {D}_{a}^{v}$
,
 $[[\lnot \mathsf {DEN}(\gamma _{ab}x_{a})]]^{\mathcal {M},u,g_{x_{a}}^{\theta }}=T$
. However,
$[[\lnot \mathsf {DEN}(\gamma _{ab}x_{a})]]^{\mathcal {M},u,g_{x_{a}}^{\theta }}=T$
. However,
 $\gamma _{ab}$
is closed and rigid and so
$\gamma _{ab}$
is closed and rigid and so
 $[[\gamma _{ab}]]^{\mathcal {M},v,g}=[[\gamma _{ab}]]^{\mathcal {M},v,g_{x_{a}}^{\theta }}=[[\gamma _{ab}]]^{\mathcal {M} ,u,g_{x_{a}}^{\theta }}$
. Therefore,
$[[\gamma _{ab}]]^{\mathcal {M},v,g}=[[\gamma _{ab}]]^{\mathcal {M},v,g_{x_{a}}^{\theta }}=[[\gamma _{ab}]]^{\mathcal {M} ,u,g_{x_{a}}^{\theta }}$
. Therefore,
 $[[\gamma _{ab}]]^{\mathcal {M} ,u,g_{x_{a}}^{\theta }}(\theta )\neq \divideontimes $
and then
$[[\gamma _{ab}]]^{\mathcal {M} ,u,g_{x_{a}}^{\theta }}(\theta )\neq \divideontimes $
and then
 $[[\mathsf {DEN }(\gamma _{ab}x_{a})]]^{\mathcal {M},u,g_{x_{a}}^{\theta }}=T$
, which is a contradiction.
$[[\mathsf {DEN }(\gamma _{ab}x_{a})]]^{\mathcal {M},u,g_{x_{a}}^{\theta }}=T$
, which is a contradiction.Case
 $(b)$
:
$(b)$
:
 $[[\gamma _{ab}]]^{\mathcal {M},v,g}=\divideontimes $
is not possible as
$[[\gamma _{ab}]]^{\mathcal {M},v,g}=\divideontimes $
is not possible as
 $[[\mathsf {DEN}(\gamma _{ab})]]^{\mathcal {M},w,g}=T$
and so there is a
$[[\mathsf {DEN}(\gamma _{ab})]]^{\mathcal {M},w,g}=T$
and so there is a
 $v^{\ast }\in W$
where
$v^{\ast }\in W$
where
 $[[\gamma _{ab}]]^{\mathcal {M} ,w,g_{s}^{w}}\in \mathsf {D}_{ab}^{v^{\ast }}$
, and so
$[[\gamma _{ab}]]^{\mathcal {M} ,w,g_{s}^{w}}\in \mathsf {D}_{ab}^{v^{\ast }}$
, and so
 $[[\gamma _{ab}]]^{ \mathcal {M},w,g_{s}^{w}}\not =\divideontimes $
. But we already noted that the interpretation of
$[[\gamma _{ab}]]^{ \mathcal {M},w,g_{s}^{w}}\not =\divideontimes $
. But we already noted that the interpretation of
 $\gamma _{ab}$
remains the same when we change worlds or pass to assignments
$\gamma _{ab}$
remains the same when we change worlds or pass to assignments
 $g^{\ast }$
that are either s-variant or
$g^{\ast }$
that are either s-variant or
 $x_{a}$
-variant of g. Therefore,
$x_{a}$
-variant of g. Therefore,
 $[[\gamma _{ab}]]^{\mathcal {M},v,g}=[[\gamma _{ab}]]^{\mathcal {M},w,g_{s}^{w}}\not =\divideontimes $
, which is a contradiction.
$[[\gamma _{ab}]]^{\mathcal {M},v,g}=[[\gamma _{ab}]]^{\mathcal {M},w,g_{s}^{w}}\not =\divideontimes $
, which is a contradiction. -
-
• Global constraints schema for kind t.
 $@_{i}(\mathsf {EXISTS}(\gamma _{ab}))\equiv \mathsf {A}(\lnot i\rightarrow \forall x_{a}(\lnot @_{i}(\mathsf {EXISTS}(x_{a}))\rightarrow \gamma _{ab}x_{a}\equiv \bot _{b})))$
, where
$@_{i}(\mathsf {EXISTS}(\gamma _{ab}))\equiv \mathsf {A}(\lnot i\rightarrow \forall x_{a}(\lnot @_{i}(\mathsf {EXISTS}(x_{a}))\rightarrow \gamma _{ab}x_{a}\equiv \bot _{b})))$
, where
 $\gamma _{ab}\in \mathsf {CME}_{ab}\cap \mathsf {RIGIDS} $
,
$\gamma _{ab}\in \mathsf {CME}_{ab}\cap \mathsf {RIGIDS} $
,
 $\langle a,b\rangle \in \mathsf {TYPES}_{t}$
. By definition:
$\langle a,b\rangle \in \mathsf {TYPES}_{t}$
. By definition:-
–
 $[[@_{i}(\mathsf {EXISTS}(\gamma _{ab}))]]^{\mathcal {M},w,g}=T$
iff
$[[@_{i}(\mathsf {EXISTS}(\gamma _{ab}))]]^{\mathcal {M},w,g}=T$
iff
 $ [[\gamma _{ab}]]^{\mathcal {M},v,g}\in \mathsf {D}_{ab}^{v}$
, with
$ [[\gamma _{ab}]]^{\mathcal {M},v,g}\in \mathsf {D}_{ab}^{v}$
, with
 $\left [ \mathsf {I}(i)\right ] (v)=T$
.
$\left [ \mathsf {I}(i)\right ] (v)=T$
. -
–
 $[[\mathsf {A}(\lnot i\rightarrow \forall x_{a}(\lnot @_{i}(\mathsf {EXISTS}(x_{a}))\rightarrow \gamma _{ab}x_{a}\equiv \bot _{b}))]]^{\mathcal {M} ,w,g}=T$
iff for all
$[[\mathsf {A}(\lnot i\rightarrow \forall x_{a}(\lnot @_{i}(\mathsf {EXISTS}(x_{a}))\rightarrow \gamma _{ab}x_{a}\equiv \bot _{b}))]]^{\mathcal {M} ,w,g}=T$
iff for all
 $w^{\prime }\in W$
,
$w^{\prime }\in W$
,
 $\left [ \mathsf {I}(i)\right ] (w^{\prime })=T$
or
$\left [ \mathsf {I}(i)\right ] (w^{\prime })=T$
or
 $[[\forall x_{a}(\lnot @_{i}(\mathsf {EXISTS} (x_{a}))\rightarrow \gamma _{ab}x_{a}\equiv \bot _{b})]]^{\mathcal {M},w^{\prime },g}=T$
.
$[[\forall x_{a}(\lnot @_{i}(\mathsf {EXISTS} (x_{a}))\rightarrow \gamma _{ab}x_{a}\equiv \bot _{b})]]^{\mathcal {M},w^{\prime },g}=T$
.
 $(\Rightarrow )$
Suppose that
$(\Rightarrow )$
Suppose that
 $[[\gamma _{ab}]]^{\mathcal {M},v,g}\in \mathsf {D}_{ab}^{v}$
. Let
$[[\gamma _{ab}]]^{\mathcal {M},v,g}\in \mathsf {D}_{ab}^{v}$
. Let
 $w^{\ast }\in W$
. In case
$w^{\ast }\in W$
. In case
 $\left [ \mathsf {I}(i)\right ] (w^{\ast })=T$
the proof is done. In case
$\left [ \mathsf {I}(i)\right ] (w^{\ast })=T$
the proof is done. In case
 $\left [ \mathsf {I}(i)\right ] (w^{\ast })=F$
the consequent of the formula will be proved. Let
$\left [ \mathsf {I}(i)\right ] (w^{\ast })=F$
the consequent of the formula will be proved. Let
 $\theta \in \mathsf {D}_{a}^{w^{\ast }}$
. Assume that
$\theta \in \mathsf {D}_{a}^{w^{\ast }}$
. Assume that
 $[[\lnot @_{i} (\mathsf {EXISTS}(x_{a}))]]^{\mathcal {M},w^{\ast },g_{x_{a}}^{\theta }}=T$
. Hence
$[[\lnot @_{i} (\mathsf {EXISTS}(x_{a}))]]^{\mathcal {M},w^{\ast },g_{x_{a}}^{\theta }}=T$
. Hence
 $\theta \not \in \mathsf {D}_{a}^{v}$
. Since
$\theta \not \in \mathsf {D}_{a}^{v}$
. Since
 $[[\gamma _{ab}]]^{\mathcal { M},v,g}\in \mathsf {D}_{ab}^{v}$
, we can apply the locality for kind t condition to get
$[[\gamma _{ab}]]^{\mathcal { M},v,g}\in \mathsf {D}_{ab}^{v}$
, we can apply the locality for kind t condition to get
 $[[\gamma _{ab}]]^{\mathcal {M},v,g}(\theta )=F_{b}$
. We have that,
$[[\gamma _{ab}]]^{\mathcal {M},v,g}(\theta )=F_{b}$
. We have that,
 $[[\gamma _{ab}]]^{\mathcal {M},w^{\ast },g_{x_{a}}^{\theta }}(\theta )= \ [[\gamma _{ab}]]^{\mathcal {M},v,g}(\theta )=F_{b}$
(because
$[[\gamma _{ab}]]^{\mathcal {M},w^{\ast },g_{x_{a}}^{\theta }}(\theta )= \ [[\gamma _{ab}]]^{\mathcal {M},v,g}(\theta )=F_{b}$
(because
 $ \gamma _{ab}$
is rigid and closed). Therefore,
$ \gamma _{ab}$
is rigid and closed). Therefore,
 $[[\gamma _{ab}x_{a}\equiv \bot _{b}]]^{\mathcal {M},w^{\ast },g_{x_{a}}^{\theta }}=T$
, as desired.
$[[\gamma _{ab}x_{a}\equiv \bot _{b}]]^{\mathcal {M},w^{\ast },g_{x_{a}}^{\theta }}=T$
, as desired. $(\Leftarrow )$
Suppose that for all
$(\Leftarrow )$
Suppose that for all
 $w^{\prime }\in W$
: If
$w^{\prime }\in W$
: If
 $\left [ \mathsf {I} (i)\right ] (w^{\prime })=F$
then for all
$\left [ \mathsf {I} (i)\right ] (w^{\prime })=F$
then for all
 $\theta \in \mathsf {D}_{a}^{w^{\prime } } $
we have that
$\theta \in \mathsf {D}_{a}^{w^{\prime } } $
we have that
 $[[(\lnot @_{i}(\mathsf {EXISTS}(x_{a}))\rightarrow \gamma _{ab}x_{a}\equiv \bot _{b})]]^{\mathcal {M},w^{\prime },g_{x_{a}}^{\theta }}=T$
. Let
$[[(\lnot @_{i}(\mathsf {EXISTS}(x_{a}))\rightarrow \gamma _{ab}x_{a}\equiv \bot _{b})]]^{\mathcal {M},w^{\prime },g_{x_{a}}^{\theta }}=T$
. Let
 $w^{\ast }\in W$
and
$w^{\ast }\in W$
and
 $w^{\ast }\not =v$
. So
$w^{\ast }\not =v$
. So
 $\left [ \mathsf {I}(i)\right ] (w^{\ast })=F$
(because
$\left [ \mathsf {I}(i)\right ] (w^{\ast })=F$
(because
 $\left [ \mathsf {I}(i)\right ] (v)=T$
). Take any
$\left [ \mathsf {I}(i)\right ] (v)=T$
). Take any
 $ \theta \in \mathsf {D}_{a}^{w^{\ast }}$
: if
$ \theta \in \mathsf {D}_{a}^{w^{\ast }}$
: if
 $\theta \not \in \mathsf {D} _{a}^{v} $
then
$\theta \not \in \mathsf {D} _{a}^{v} $
then
 $[[\gamma _{ab}]]^{\mathcal {M},w^{\ast },g_{x_{a}}^{\theta }}(\theta )=F_{b}$
. So,
$[[\gamma _{ab}]]^{\mathcal {M},w^{\ast },g_{x_{a}}^{\theta }}(\theta )=F_{b}$
. So,
 $[[\gamma _{ab}]]^{\mathcal {M},v,g}(\theta )=F_{b}$
(because
$[[\gamma _{ab}]]^{\mathcal {M},v,g}(\theta )=F_{b}$
(because
 $\gamma _{ab}$
is rigid and closed and Proposition 2.12). We want to see that
$\gamma _{ab}$
is rigid and closed and Proposition 2.12). We want to see that
 $[[@_{i}(\mathsf {EXISTS}(\gamma _{ab}))]]^{\mathcal {M} ,w,g}=T$
. In the first place, being a general structure,
$[[@_{i}(\mathsf {EXISTS}(\gamma _{ab}))]]^{\mathcal {M} ,w,g}=T$
. In the first place, being a general structure,
 $[[\gamma _{ab}]]^{ \mathcal {M},v,g}\in \mathsf {D}_{ab}$
, as this expression is of kind t. Moreover, we just saw that it satisfies the locality for kind t condition because for all
$[[\gamma _{ab}]]^{ \mathcal {M},v,g}\in \mathsf {D}_{ab}$
, as this expression is of kind t. Moreover, we just saw that it satisfies the locality for kind t condition because for all
 $\theta \in \mathsf {D}_{a}-\mathsf {D} _{a}^{v}$
the value of the function is
$\theta \in \mathsf {D}_{a}-\mathsf {D} _{a}^{v}$
the value of the function is
 $F_{b}$
. Therefore,
$F_{b}$
. Therefore,
 $[[\gamma _{ab}]]^{\mathcal {M},v,g}\in \mathsf {D}_{ab}^{v}$
and so
$[[\gamma _{ab}]]^{\mathcal {M},v,g}\in \mathsf {D}_{ab}^{v}$
and so
 $[[@_{i}(\mathsf { EXISTS}(\gamma _{ab}))]]^{\mathcal {M},w,g}=T$
, as desired.
$[[@_{i}(\mathsf { EXISTS}(\gamma _{ab}))]]^{\mathcal {M},w,g}=T$
, as desired. -
7 Maximal consistency and saturation
We begin by recalling some standard definitions and results for classical logic:
Definition 7.1 (Maximal consistency).
Let
![]() $\Sigma \subseteq \ \mathsf {ME}_t$
be a set of meaningful expressions of type t. Then:
$\Sigma \subseteq \ \mathsf {ME}_t$
be a set of meaningful expressions of type t. Then:
-
(1)
 $\Sigma $
is inconsistent iff for every
$\Sigma $
is inconsistent iff for every
 $\varphi \in \mathsf {ME}_t$
,
$\varphi \in \mathsf {ME}_t$
,
 $\Sigma \vdash \varphi $
.
$\Sigma \vdash \varphi $
. -
(2)
 $\Sigma $
is consistent iff it is not inconsistent.
$\Sigma $
is consistent iff it is not inconsistent. -
(3)
 $\Sigma $
is a maximal consistent set iff
$\Sigma $
is a maximal consistent set iff
 $\Sigma $
is consistent and whenever
$\Sigma $
is consistent and whenever
 $\varphi \in \mathsf {ME}_t$
and
$\varphi \in \mathsf {ME}_t$
and
 $\varphi \notin \Sigma $
, then
$\varphi \notin \Sigma $
, then
 $\Sigma \cup \{\varphi \}$
is inconsistent.
$\Sigma \cup \{\varphi \}$
is inconsistent.
Lemma 7.2. Let
![]() $\Delta , \Gamma \subseteq {\mathsf {ME}}_t$
be maximal consistent sets and
$\Delta , \Gamma \subseteq {\mathsf {ME}}_t$
be maximal consistent sets and
![]() $ \varphi $
,
$ \varphi $
,
![]() $\psi \in {\mathsf {ME}}_t$
. Then all the following hold:
$\psi \in {\mathsf {ME}}_t$
. Then all the following hold:
-
(1) If
 $\Delta $
is consistent and
$\Delta $
is consistent and
 $\Gamma \subseteq \Delta $
, then
$\Gamma \subseteq \Delta $
, then
 $\Gamma $
is consistent.
$\Gamma $
is consistent. -
(2) If
 $\Delta $
is inconsistent and
$\Delta $
is inconsistent and
 $\Delta \subseteq \Gamma $
, then
$\Delta \subseteq \Gamma $
, then
 $ \Gamma $
is inconsistent.
$ \Gamma $
is inconsistent. -
(3)
 $\Delta \subseteq \mathsf {ME}_t$
is inconsistent iff there is a
$\Delta \subseteq \mathsf {ME}_t$
is inconsistent iff there is a
 $\varphi \in \mathsf {ME}_t$
such that
$\varphi \in \mathsf {ME}_t$
such that
 $\Delta \vdash \varphi $
and
$\Delta \vdash \varphi $
and
 $ \Delta \vdash \lnot \varphi $
.
$ \Delta \vdash \lnot \varphi $
. -
(4)
 $\Delta \subseteq \mathsf {ME}_t$
is inconsistent iff
$\Delta \subseteq \mathsf {ME}_t$
is inconsistent iff
 $\Delta \vdash \bot $
.
$\Delta \vdash \bot $
. -
(5) If
 $\Delta $
is consistent, then for all
$\Delta $
is consistent, then for all
 $\varphi \in \mathsf {ME}_t$
such that
$\varphi \in \mathsf {ME}_t$
such that
 $\Delta \vdash \varphi $
then
$\Delta \vdash \varphi $
then
 $\Delta \cup \left \{ \varphi \right \}$
is consistent.
$\Delta \cup \left \{ \varphi \right \}$
is consistent. -
(6)
 $\Delta $
is consistent iff every finite subset of
$\Delta $
is consistent iff every finite subset of
 $\Delta $
is consistent.
$\Delta $
is consistent. -
(7) If each subset of
 $\Delta $
has a model, then it is consistent, assuming soundness.
$\Delta $
has a model, then it is consistent, assuming soundness.
Lemma 7.3. Let
![]() $\Delta \subseteq {\mathsf {ME}} _t $
be a maximal consistent set and
$\Delta \subseteq {\mathsf {ME}} _t $
be a maximal consistent set and
![]() $\varphi $
,
$\varphi $
,
![]() $\psi \in {\mathsf {ME }}_t$
. Then all the following hold:
$\psi \in {\mathsf {ME }}_t$
. Then all the following hold:
-
(1)
 $\Delta \vdash \varphi $
iff
$\Delta \vdash \varphi $
iff
 $\varphi \in \Delta $
.
$\varphi \in \Delta $
. -
(2) If
 $\vdash \varphi $
then
$\vdash \varphi $
then
 $\varphi \in \Delta $
.
$\varphi \in \Delta $
. -
(3)
 $\lnot \varphi \in \Delta $
iff
$\lnot \varphi \in \Delta $
iff
 $\varphi \notin \Delta $
.
$\varphi \notin \Delta $
. -
(4)
 $\varphi \in \Delta $
iff
$\varphi \in \Delta $
iff
 $\lnot \varphi \not \in \Delta $
.
$\lnot \varphi \not \in \Delta $
. -
(5)
 $\varphi \wedge \psi \in \Delta $
iff
$\varphi \wedge \psi \in \Delta $
iff
 $\varphi \in \Delta $
and
$\varphi \in \Delta $
and
 $\psi \in \Delta $
.
$\psi \in \Delta $
. -
(6) Either
 $\varphi \in \Delta $
or
$\varphi \in \Delta $
or
 $\lnot \varphi \in \Delta $
but not both.
$\lnot \varphi \in \Delta $
but not both. -
(7) If
 $\Delta \cup \{\varphi \}\vdash \psi $
and
$\Delta \cup \{\varphi \}\vdash \psi $
and
 $\Delta \cup \{\psi \}\vdash \varphi $
then
$\Delta \cup \{\psi \}\vdash \varphi $
then
 $\varphi \in \Delta $
iff
$\varphi \in \Delta $
iff
 $\psi \in \Delta $
.
$\psi \in \Delta $
.
However the next concept, which was introduced in [Reference Areces, Blackburn, Huertas and Manzano2, Reference Blackburn, Huertas, Manzano, Jørgensen, Manzano, Sain and Alonso6], is specifically about hybrid type theory:
Definition 7.4 (Saturation).
Let
![]() $\Sigma $
be a set of meaningful expressions. Then:
$\Sigma $
be a set of meaningful expressions. Then:
-
(1)
 $\Sigma $
is named iff one of its elements is a nominal.
$\Sigma $
is named iff one of its elements is a nominal. -
(2)
 $\Sigma $
is
$\Sigma $
is
 $\Diamond $
-saturated iff for any formula
$\Diamond $
-saturated iff for any formula
 $ @_i\Diamond \varphi \in \Sigma $
there is a nominal
$ @_i\Diamond \varphi \in \Sigma $
there is a nominal
 $j\in \mathsf {NOM}$
such that
$j\in \mathsf {NOM}$
such that
 $@_i\Diamond j\in \Sigma $
and
$@_i\Diamond j\in \Sigma $
and
 $@_{j}\varphi \in \Sigma $
.
$@_{j}\varphi \in \Sigma $
. -
(3)
 $\Sigma $
is
$\Sigma $
is
 $\mathsf {E}$
-saturated iff for any formula
$\mathsf {E}$
-saturated iff for any formula
 $@_{i} \mathsf {E}\varphi \in \Sigma $
there is a nominal
$@_{i} \mathsf {E}\varphi \in \Sigma $
there is a nominal
 $j\in \mathsf {NOM}$
such that
$j\in \mathsf {NOM}$
such that
 $@_{i}\mathsf {E}j\in \Sigma $
and
$@_{i}\mathsf {E}j\in \Sigma $
and
 $@_{j}\varphi \in \Sigma $
.Footnote
8
$@_{j}\varphi \in \Sigma $
.Footnote
8
-
(4)
 $\Sigma $
is
$\Sigma $
is
 $\exists $
-saturated iff for any formula
$\exists $
-saturated iff for any formula
 $@_i\exists x_a\varphi \in \Sigma $
there is a constant
$@_i\exists x_a\varphi \in \Sigma $
there is a constant
 $c_a$
such that
$c_a$
such that
 $@_i(\mathsf { EXISTS}(c_a))\in \Sigma $
and
$@_i(\mathsf { EXISTS}(c_a))\in \Sigma $
and
 $@_i\varphi \frac {@_ic_a}{x_a}\in \Sigma $
.
$@_i\varphi \frac {@_ic_a}{x_a}\in \Sigma $
.
Saturated maximal consistent sets are important, because maximal consistent sets that are
![]() $\Diamond $
-saturated,
$\Diamond $
-saturated,
![]() $\mathsf {E}$
-saturated, and
$\mathsf {E}$
-saturated, and
![]() $\exists $
-saturated provide suitable Henkin-style witnesses for
$\exists $
-saturated provide suitable Henkin-style witnesses for
![]() $ \Diamond $
,
$ \Diamond $
,
![]() $\mathsf {E}$
, and
$\mathsf {E}$
, and
![]() $\exists $
, respectively. Note, however, that we do not provide any witnesses for
$\exists $
, respectively. Note, however, that we do not provide any witnesses for
![]() ${\downarrow }$
. This is unnecessary because of the following lemma:
${\downarrow }$
. This is unnecessary because of the following lemma:
Lemma 7.5. Let
![]() $\Delta $
be maximal consistent, and let i be any nominal such that
$\Delta $
be maximal consistent, and let i be any nominal such that
![]() $i\in \Delta $
. Then we have that
$i\in \Delta $
. Then we have that
![]() $@_{i}{{\downarrow \hspace {-0.1 pt}} } s\varphi \in \Delta $
iff
$@_{i}{{\downarrow \hspace {-0.1 pt}} } s\varphi \in \Delta $
iff
![]() $@_{i}\varphi (\frac {i}{s})\in \Delta $
.
$@_{i}\varphi (\frac {i}{s})\in \Delta $
.
Proof Recall that the DA schema (Axiom 7) is
![]() $@_{i}({\downarrow \hspace {-0.1 pt}} s\varphi \equiv \varphi (\frac {i}{s}))$
, so we have
$@_{i}({\downarrow \hspace {-0.1 pt}} s\varphi \equiv \varphi (\frac {i}{s}))$
, so we have
![]() $\vdash @_{i}({{\downarrow \hspace {-0.1 pt}} }s\varphi )\equiv @_{i}(\varphi (\frac {i}{s}))$
, by Equality-at-named-worlds (Axiom 5a). Hence
$\vdash @_{i}({{\downarrow \hspace {-0.1 pt}} }s\varphi )\equiv @_{i}(\varphi (\frac {i}{s}))$
, by Equality-at-named-worlds (Axiom 5a). Hence
![]() $@_{i}{{\downarrow \hspace {-0.1 pt}} }s\varphi \in \Delta $
iff
$@_{i}{{\downarrow \hspace {-0.1 pt}} }s\varphi \in \Delta $
iff
![]() $@_{i}\varphi (\frac {i}{s})\in \Delta $
.
$@_{i}\varphi (\frac {i}{s})\in \Delta $
.
8 Lindenbaum lemma
In this section we state and prove the Lindenbaum lemma we shall use. The basic idea is familiar from Henkin-style completeness proofs for first-order logic: inductively add new constants c to witness existential statements. In the following proof both higher-order constants and nominals are inductively added. The higher-order constants
![]() $c_{a}$
are used to witness higher-order existential statements, but they are first prefixed by an expression of the form
$c_{a}$
are used to witness higher-order existential statements, but they are first prefixed by an expression of the form
![]() $@_{i}$
to rigidify them: the upshot is that every higher-order existential statement ends up being rigidly witnessed. In addition, new nominals are used to witness formulas prefixed by the
$@_{i}$
to rigidify them: the upshot is that every higher-order existential statement ends up being rigidly witnessed. In addition, new nominals are used to witness formulas prefixed by the
![]() $ \Diamond $
and
$ \Diamond $
and
![]() $\mathsf {E}$
modalities (a standard technique in completeness proofs for propositional and first-order hybrid logic).
$\mathsf {E}$
modalities (a standard technique in completeness proofs for propositional and first-order hybrid logic).
Lemma 8.1 (Lindenbaum).
Any consistent set of sentences
![]() $\Gamma $
can be extended to a maximal consistent set
$\Gamma $
can be extended to a maximal consistent set
![]() $\Gamma ^\ast $
that is named,
$\Gamma ^\ast $
that is named,
![]() $\Diamond $
-saturated,
$\Diamond $
-saturated,
![]() $\mathsf {E }$
-saturated, and
$\mathsf {E }$
-saturated, and
![]() $\exists $
-saturated.
$\exists $
-saturated.
Proof We first construct the set
![]() $\Gamma ^\ast $
. Let
$\Gamma ^\ast $
. Let
![]() $\left \{ i_{n}\right \} _{n\in \omega }$
be an enumeration of a countably infinite set of new nominals, let
$\left \{ i_{n}\right \} _{n\in \omega }$
be an enumeration of a countably infinite set of new nominals, let
![]() $ \left \{ c_{n,a}\right \}_{n\in \omega }$
be an enumeration of a countably infinite set of new constants of each type a, and let
$ \left \{ c_{n,a}\right \}_{n\in \omega }$
be an enumeration of a countably infinite set of new constants of each type a, and let
![]() $\left \{ \varphi _{n}\right \}_{n\in \omega }$
an enumeration of the expressions of type t of the extended language. We will build a family of subsets of
$\left \{ \varphi _{n}\right \}_{n\in \omega }$
an enumeration of the expressions of type t of the extended language. We will build a family of subsets of
![]() $ \mathsf {ME}_t$
,
$ \mathsf {ME}_t$
,
![]() $\{\Gamma _{n}\}_{n\in \omega }$
by induction:
$\{\Gamma _{n}\}_{n\in \omega }$
by induction:
-
•
 $\Gamma ^{0}=\Gamma \cup \left \{ i_{0}\right \} $
.
$\Gamma ^{0}=\Gamma \cup \left \{ i_{0}\right \} $
. -
• Assume that
 $\Gamma ^{n}$
has been built already. To define
$\Gamma ^{n}$
has been built already. To define
 $\Gamma ^{n+1}$
we distinguish five cases:
$\Gamma ^{n+1}$
we distinguish five cases:-
(1)
 $\Gamma ^{n+1}=\Gamma ^{n}$
, if
$\Gamma ^{n+1}=\Gamma ^{n}$
, if
 $\Gamma ^{n}\cup \left \{ \varphi _{n}\right \} $
is inconsistent.
$\Gamma ^{n}\cup \left \{ \varphi _{n}\right \} $
is inconsistent. -
(2)
 $\Gamma ^{n+1}= \ \Gamma ^{n}\cup \left \{ \varphi _{n}\right \}$
, if
$\Gamma ^{n+1}= \ \Gamma ^{n}\cup \left \{ \varphi _{n}\right \}$
, if  $$ \begin{align*} \left\{ \begin{array}{l} \Gamma ^{n}\cup \left\{ \varphi _{n}\right\} \ \ \text{is consistent and} \\ \varphi _{n}\ \text{is not of the form }@_{i}\Diamond \psi \text{ or } @_{i}\exists x_{a}\psi \text{ or }@_{i}\mathsf{E}\psi. \end{array} \right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{array}{l} \Gamma ^{n}\cup \left\{ \varphi _{n}\right\} \ \ \text{is consistent and} \\ \varphi _{n}\ \text{is not of the form }@_{i}\Diamond \psi \text{ or } @_{i}\exists x_{a}\psi \text{ or }@_{i}\mathsf{E}\psi. \end{array} \right. \end{align*} $$
-
(3)
 $\Gamma ^{n+1}=\Gamma ^{n}\cup \{\varphi _{n},@_{i}\Diamond i_{m},@_{i_{m}}\psi \}$
, if
$\Gamma ^{n+1}=\Gamma ^{n}\cup \{\varphi _{n},@_{i}\Diamond i_{m},@_{i_{m}}\psi \}$
, if  $$ \begin{align*} \left\{ \begin{array}{c} \Gamma ^{n}\cup \left\{ \varphi _{n}\right\} \ \ \text{is consistent,} \ \varphi _{n}:=@_{i}\Diamond \psi \text{ and} \\ i_{m}\text{ is the first new nominal not in }\Gamma ^{n}\text{ or }\varphi_{n}. \end{array} \right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{array}{c} \Gamma ^{n}\cup \left\{ \varphi _{n}\right\} \ \ \text{is consistent,} \ \varphi _{n}:=@_{i}\Diamond \psi \text{ and} \\ i_{m}\text{ is the first new nominal not in }\Gamma ^{n}\text{ or }\varphi_{n}. \end{array} \right. \end{align*} $$
-
(4)
 $\Gamma ^{n+1}=\Gamma ^{n}\cup \{\varphi _{n},@_{i}\mathsf {E} i_{m},@_{i_{m}}\psi \}$
, if
$\Gamma ^{n+1}=\Gamma ^{n}\cup \{\varphi _{n},@_{i}\mathsf {E} i_{m},@_{i_{m}}\psi \}$
, if  $$ \begin{align*} \left\{ \begin{array}{c} \Gamma ^{n}\cup \left\{ \varphi _{n}\right\} \ \ \text{is consistent,} \ \varphi _{n}:=@_{i}\mathsf{E}\psi \text{ and} \\ i_{m}\text{ is the first new nominal not in }\Gamma ^{n}\text{ or }\varphi_{n}. \end{array} \right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{array}{c} \Gamma ^{n}\cup \left\{ \varphi _{n}\right\} \ \ \text{is consistent,} \ \varphi _{n}:=@_{i}\mathsf{E}\psi \text{ and} \\ i_{m}\text{ is the first new nominal not in }\Gamma ^{n}\text{ or }\varphi_{n}. \end{array} \right. \end{align*} $$
-
(5)
 $\Gamma ^{n+1}=\Gamma ^{n}\cup \{\varphi _{n},@_{i}(\mathsf {EXISTS}(c_{m,a})),@_{i}\psi \frac {@_{i}c_{m,a}}{x_{a}}\}$
, if
$\Gamma ^{n+1}=\Gamma ^{n}\cup \{\varphi _{n},@_{i}(\mathsf {EXISTS}(c_{m,a})),@_{i}\psi \frac {@_{i}c_{m,a}}{x_{a}}\}$
, if  $$ \begin{align*} \left\{ \begin{array}{l} \Gamma ^{n}\cup \left\{ \varphi _{n}\right\} \ \ \text{is consistent,} \ \varphi _{n}:=@_{i}\exists x_{a}\psi \\ c_{m,a}\text{ is the first new constant of type } a\text{ not in }\Gamma ^{n} \text{ or }\varphi _{n}. \end{array} \right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{array}{l} \Gamma ^{n}\cup \left\{ \varphi _{n}\right\} \ \ \text{is consistent,} \ \varphi _{n}:=@_{i}\exists x_{a}\psi \\ c_{m,a}\text{ is the first new constant of type } a\text{ not in }\Gamma ^{n} \text{ or }\varphi _{n}. \end{array} \right. \end{align*} $$
-
Let
![]() $\Gamma ^\ast =\underset {n\in \omega }{\cup }\Gamma ^{n}$
.
$\Gamma ^\ast =\underset {n\in \omega }{\cup }\Gamma ^{n}$
.
To prove that
![]() $\Gamma ^\ast $
is named,
$\Gamma ^\ast $
is named,
![]() $\Diamond $
-saturated,
$\Diamond $
-saturated,
![]() $\exists $
-saturated,
$\exists $
-saturated,
![]() ${\mathsf {E}}$
-saturated. and maximal consistent, one follows the standard procedure, as can be seen in Appendix 12.3.
${\mathsf {E}}$
-saturated. and maximal consistent, one follows the standard procedure, as can be seen in Appendix 12.3.
9 Constructing the induced structure
In this section we show how to build a structure
![]() $\mathcal {M}$
(as defined in Definition 2.5) using the information in a maximal consistent set of sentences
$\mathcal {M}$
(as defined in Definition 2.5) using the information in a maximal consistent set of sentences
![]() $\Gamma ^\ast $
that is named,
$\Gamma ^\ast $
that is named,
![]() $\Diamond $
-saturated,
$\Diamond $
-saturated,
![]() $\exists $
-saturated, and
$\exists $
-saturated, and
![]() $\mathsf {E}$
-saturated. That is, we will define the
$\mathsf {E}$
-saturated. That is, we will define the
![]() $\mathcal {HPTT}$
model
$\mathcal {HPTT}$
model
![]() $\mathcal {M}=\langle \mathcal {S},\mathsf {I} \rangle $
induced by
$\mathcal {M}=\langle \mathcal {S},\mathsf {I} \rangle $
induced by
![]() $\Gamma ^\ast $
, having a skeleton
$\Gamma ^\ast $
, having a skeleton
and a denotation function
![]() $\mathsf {I}$
. We begin with the easiest part: defining the worlds W and the accessibility relation R.
$\mathsf {I}$
. We begin with the easiest part: defining the worlds W and the accessibility relation R.
9.1 Defining W and R
We first define an equivalence relation for nominals as follows: for all
![]() $ i,j\in \mathsf {NOM}$
, we define
$ i,j\in \mathsf {NOM}$
, we define
![]() $i\approx j$
iff
$i\approx j$
iff
![]() $@_ij\in \Gamma ^\ast $
. We want our set of worlds W to be the set of equivalence classes induced by
$@_ij\in \Gamma ^\ast $
. We want our set of worlds W to be the set of equivalence classes induced by
![]() $\approx $
, so we first check that
$\approx $
, so we first check that
![]() $\approx $
is an equivalence relation.
$\approx $
is an equivalence relation.
Proposition 9.1. The relation
![]() $\approx $
is an equivalence relation on
$\approx $
is an equivalence relation on
![]() $\mathsf {NOM}$
.
$\mathsf {NOM}$
.
Proof A straightforward exercise in propositional hybrid logic.
Definition 9.2. Let
![]() $[i]=\{j\in \mathsf {NOM}\mid i\approx j\}$
. We define the set of worlds
$[i]=\{j\in \mathsf {NOM}\mid i\approx j\}$
. We define the set of worlds
![]() ${W=\{[i]:i\in \mathsf {NOM}\}}$
, and the accessibility relation
${W=\{[i]:i\in \mathsf {NOM}\}}$
, and the accessibility relation
![]() $R=\{\langle \lbrack [i],[j]\rangle \mid @_{i}\Diamond j\in \Gamma ^{\ast }\}$
.
$R=\{\langle \lbrack [i],[j]\rangle \mid @_{i}\Diamond j\in \Gamma ^{\ast }\}$
.
Proposition 9.3. R is a well-defined relation. In particular:
-
(1)
 $i\approx i^{\prime }$
and
$i\approx i^{\prime }$
and
 $\langle \left [ i\right ] ,\left [ j\right ] \rangle \in R$
implies
$\langle \left [ i\right ] ,\left [ j\right ] \rangle \in R$
implies
 $\langle \left [ i^{\prime }\right ] ,\left [ j\right ] \rangle \in R$
.
$\langle \left [ i^{\prime }\right ] ,\left [ j\right ] \rangle \in R$
. -
(2)
 $j\approx j^{\prime }$
and
$j\approx j^{\prime }$
and
 $\langle \left [ i\right ] ,\left [ j\right ] \rangle \in R$
implies
$\langle \left [ i\right ] ,\left [ j\right ] \rangle \in R$
implies
 $\langle \left [ i\right ] ,\left [ j^{\prime }\right ] \rangle \in R$
.
$\langle \left [ i\right ] ,\left [ j^{\prime }\right ] \rangle \in R$
.
Proof The first claim follows because
![]() $@_{i}i^{\prime }\rightarrow \left ( @_{i}\Diamond j\rightarrow @_{i^{\prime }}\Diamond j\right ) $
is provable by Axiom 3c, rule Gen
$@_{i}i^{\prime }\rightarrow \left ( @_{i}\Diamond j\rightarrow @_{i^{\prime }}\Diamond j\right ) $
is provable by Axiom 3c, rule Gen
![]() $_{@}$
, and Axioms 1c and 3d, and so belongs to
$_{@}$
, and Axioms 1c and 3d, and so belongs to
![]() $\Gamma ^{\ast }$
. Thus, as
$\Gamma ^{\ast }$
. Thus, as
![]() $@_{i}i^{\prime }\in \Gamma ^{\ast }$
and
$@_{i}i^{\prime }\in \Gamma ^{\ast }$
and
![]() $@_{i}\Diamond j\in \Gamma ^{\ast }$
, we have that
$@_{i}\Diamond j\in \Gamma ^{\ast }$
, we have that
![]() $ @_{i^{\prime }}\Diamond j\in \Gamma ^{\ast }$
(as
$ @_{i^{\prime }}\Diamond j\in \Gamma ^{\ast }$
(as
![]() $\Gamma ^{\ast }$
is closed under Modus Ponens). The second claim follows because
$\Gamma ^{\ast }$
is closed under Modus Ponens). The second claim follows because
![]() $@_{i}\Diamond j\wedge @_{j}j^{\prime }\rightarrow @_{i}\Diamond j^{\prime }$
is the Bridge
$@_{i}\Diamond j\wedge @_{j}j^{\prime }\rightarrow @_{i}\Diamond j^{\prime }$
is the Bridge
![]() $ _{\Diamond }$
theorem (page 14) and so belongs to
$ _{\Diamond }$
theorem (page 14) and so belongs to
![]() $\Gamma ^{\ast }$
. Thus, as
$\Gamma ^{\ast }$
. Thus, as
![]() $@_{i}\Diamond j\in \Gamma ^{\ast }$
and
$@_{i}\Diamond j\in \Gamma ^{\ast }$
and
![]() $@_{j}j^{\prime }\in \Gamma ^{\ast }$
, we have that
$@_{j}j^{\prime }\in \Gamma ^{\ast }$
, we have that
![]() $@_{i}\Diamond j^{\prime }\in \Gamma ^{\ast }$
, as required.
$@_{i}\Diamond j^{\prime }\in \Gamma ^{\ast }$
, as required.
9.2 Defining the partial type hierarchies
Now for the tricky part: defining the partial type hierarchy
![]() $\langle \mathsf {D}_{a}\rangle _{a\in \mathsf {TYPES}}$
and the local partial type hierarchy
$\langle \mathsf {D}_{a}\rangle _{a\in \mathsf {TYPES}}$
and the local partial type hierarchy
![]() $\langle \mathsf {D}_{a}^{w}\rangle _{\langle w,a\rangle \in W\times \mathsf {TYPES}}$
. Our approach (which makes heavy use of ideas drawn from both Henkin [Reference Henkin16] and Farmer [Reference Farmer10]) is to define the hierarchies by induction on
$\langle \mathsf {D}_{a}^{w}\rangle _{\langle w,a\rangle \in W\times \mathsf {TYPES}}$
. Our approach (which makes heavy use of ideas drawn from both Henkin [Reference Henkin16] and Farmer [Reference Farmer10]) is to define the hierarchies by induction on
![]() $a\in \mathsf {TYPES}$
and simultaneously to define a mapping
$a\in \mathsf {TYPES}$
and simultaneously to define a mapping
![]() $\Phi $
of closed meaningful expressions onto the domains that satisfy the six conditions listed in Figure 2.
$\Phi $
of closed meaningful expressions onto the domains that satisfy the six conditions listed in Figure 2.

Figure 2 The six conditions imposed in the
![]() $\mathcal {HPTT}$
model construction.
$\mathcal {HPTT}$
model construction.
We will define the partial type hierarchies in four steps: for type t, type e, kind e, and kind t.
Definition 9.4 (Type t).
We define
![]() $\Phi $
,
$\Phi $
,
![]() $\mathsf {D}_{t}$
, and
$\mathsf {D}_{t}$
, and
![]() $\mathsf {D}_{t}^{\left [ i\right ] }$
as follows:
$\mathsf {D}_{t}^{\left [ i\right ] }$
as follows:
-
• Let
 $\varphi \in \mathsf {CME}_t$
. If
$\varphi \in \mathsf {CME}_t$
. If
 $\Gamma ^\ast \vdash \varphi $
, then
$\Gamma ^\ast \vdash \varphi $
, then
 $\Phi (\varphi )=T$
; otherwise
$\Phi (\varphi )=T$
; otherwise
 $\Phi (\varphi )=F$
.
$\Phi (\varphi )=F$
. -
•
 $\mathsf {D}_t=\left \{ T,F\right \}$
is the set of truth values.
$\mathsf {D}_t=\left \{ T,F\right \}$
is the set of truth values. -
•
 $\mathsf {D}_{t}^{\left [ i\right ] }=\left \{ T,F\right \} $
.
$\mathsf {D}_{t}^{\left [ i\right ] }=\left \{ T,F\right \} $
.
Proposition 9.5 (Type t).
Let
![]() $\Phi $
,
$\Phi $
,
![]() $\mathsf {D}_{t}$
, and
$\mathsf {D}_{t}$
, and
![]() $\mathsf {D}_{t}^{\left [ i\right ] }$
be as just defined. Then the six conditions in Figure 2 hold.
$\mathsf {D}_{t}^{\left [ i\right ] }$
be as just defined. Then the six conditions in Figure 2 hold.
Proof We establish the six items as follows:
-
(1) By definition,
 $\mathsf {D}_{t}=\{T,F\}$
. We will prove that
$\mathsf {D}_{t}=\{T,F\}$
. We will prove that $\{T,F\} = \left \{ \Phi (\varphi )\mid \varphi \in \mathsf {CME}_{t}\cap \mathsf {RIGIDS}\text { and }\Gamma ^{\ast }\vdash \mathsf {DEN}(\varphi )\right \}$
.
$\{T,F\} = \left \{ \Phi (\varphi )\mid \varphi \in \mathsf {CME}_{t}\cap \mathsf {RIGIDS}\text { and }\Gamma ^{\ast }\vdash \mathsf {DEN}(\varphi )\right \}$
.First, we show that
 $\{T,F\}\subseteq \{ \Phi (\varphi )\mid \varphi \in \mathsf {CME} _{t}\cap \mathsf {RIGIDS}\text { and }\Gamma ^{\ast }\vdash \mathsf {DEN}(\varphi ) \}$
. Clearly,
$\{T,F\}\subseteq \{ \Phi (\varphi )\mid \varphi \in \mathsf {CME} _{t}\cap \mathsf {RIGIDS}\text { and }\Gamma ^{\ast }\vdash \mathsf {DEN}(\varphi ) \}$
. Clearly,
 $\bot \in \mathsf {CME}_{t}\cap \mathsf {RIGIDS}$
,
$\bot \in \mathsf {CME}_{t}\cap \mathsf {RIGIDS}$
,
 $\Gamma ^{\ast }\vdash \mathsf {DEN}(\bot )$
by Axiom 8b, and
$\Gamma ^{\ast }\vdash \mathsf {DEN}(\bot )$
by Axiom 8b, and
 $\Phi (\bot )=F$
by the consistency of
$\Phi (\bot )=F$
by the consistency of
 $\Gamma ^{\ast }$
. Thus,
$\Gamma ^{\ast }$
. Thus,
 $F\in \{ \Phi (\varphi )\mid \varphi \in \mathsf {CME}_{t}\cap \mathsf {RIGIDS}\text{and }\Gamma ^{\ast }\vdash \mathsf {DEN}(\varphi ) \}$
. We also prove it for T using a similar reasoning.
$F\in \{ \Phi (\varphi )\mid \varphi \in \mathsf {CME}_{t}\cap \mathsf {RIGIDS}\text{and }\Gamma ^{\ast }\vdash \mathsf {DEN}(\varphi ) \}$
. We also prove it for T using a similar reasoning.Secondly, we have that either
 $\Phi (\varphi )=T$
or
$\Phi (\varphi )=T$
or
 $\Phi (\varphi )=F$
for every
$\Phi (\varphi )=F$
for every
 $\varphi \in \mathsf {CME}_{t}$
, because by maximality either
$\varphi \in \mathsf {CME}_{t}$
, because by maximality either
 $\Gamma ^{\ast }\vdash \varphi $
or
$\Gamma ^{\ast }\vdash \varphi $
or
 $\Gamma ^{\ast }\vdash \lnot \varphi $
.
$\Gamma ^{\ast }\vdash \lnot \varphi $
. -
(2) On the one hand, by definition
 $\Phi (\varphi )\not =\mathsf {\ \divideontimes }$
for any
$\Phi (\varphi )\not =\mathsf {\ \divideontimes }$
for any
 $\varphi \in \mathsf {CME}_{t}$
. On the other hand, since
$\varphi \in \mathsf {CME}_{t}$
. On the other hand, since
 $\Gamma ^{\ast }\vdash \mathsf {DEN}(\varphi )$
(by Axiom 8b) and
$\Gamma ^{\ast }\vdash \mathsf {DEN}(\varphi )$
(by Axiom 8b) and
 $\Gamma ^{\ast }$
is maximal consistent,
$\Gamma ^{\ast }$
is maximal consistent,
 $\Gamma ^{\ast }\not \vdash \lnot \mathsf {DEN}(\varphi )$
for any
$\Gamma ^{\ast }\not \vdash \lnot \mathsf {DEN}(\varphi )$
for any
 $\varphi \in \mathsf {CME}_{t}$
. Thus,
$\varphi \in \mathsf {CME}_{t}$
. Thus,
 $\Phi (\varphi )=\mathsf {\divideontimes }$
iff
$\Phi (\varphi )=\mathsf {\divideontimes }$
iff
 $ \Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(\varphi )$
.
$ \Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(\varphi )$
. -
(3) Let
 $\varphi $
,
$\varphi $
,
 $\psi \in \mathsf {CME}_{t}\cap \mathsf {RIGIDS}$
. On the one hand, by using the definitions and the properties of maximal consistent sets, it is easy to see that (1) if
$\psi \in \mathsf {CME}_{t}\cap \mathsf {RIGIDS}$
. On the one hand, by using the definitions and the properties of maximal consistent sets, it is easy to see that (1) if
 $\Phi (\varphi )=T=\Phi (\psi )$
then
$\Phi (\varphi )=T=\Phi (\psi )$
then
 $\Gamma ^{\ast }\vdash \varphi $
and
$\Gamma ^{\ast }\vdash \varphi $
and
 $\Gamma ^{\ast }\vdash \psi $
and so
$\Gamma ^{\ast }\vdash \psi $
and so
 $\Gamma ^{\ast }\vdash \varphi \equiv \psi $
, and (2) if
$\Gamma ^{\ast }\vdash \varphi \equiv \psi $
, and (2) if
 $ \Phi (\varphi )=F=\Phi (\psi )$
then
$ \Phi (\varphi )=F=\Phi (\psi )$
then
 $\Gamma ^{\ast }\vdash \lnot \varphi $
and
$\Gamma ^{\ast }\vdash \lnot \varphi $
and
 $\Gamma ^{\ast }\vdash \lnot \psi $
and so
$\Gamma ^{\ast }\vdash \lnot \psi $
and so
 $\Gamma ^{\ast }\vdash \varphi \equiv \psi $
. On the other hand, if
$\Gamma ^{\ast }\vdash \varphi \equiv \psi $
. On the other hand, if
 $\Gamma ^{\ast }\vdash \varphi \equiv \psi $
then it is impossible to have
$\Gamma ^{\ast }\vdash \varphi \equiv \psi $
then it is impossible to have
 $\Phi (\varphi )=T$
and
$\Phi (\varphi )=T$
and
 $\Phi (\psi )=F$
. For
$\Phi (\psi )=F$
. For
 $\Phi (\varphi )=T$
implies
$\Phi (\varphi )=T$
implies
 $\Gamma ^{\ast }\vdash \varphi $
and so
$\Gamma ^{\ast }\vdash \varphi $
and so
 $\Gamma ^{\ast }\vdash \psi $
too, which means that
$\Gamma ^{\ast }\vdash \psi $
too, which means that
 $\Phi (\psi )=T$
as well.
$\Phi (\psi )=T$
as well. -
(4) By definition,
 $\mathsf {D}_{t}^{\left [ i\right ] }=\{T,F\}$
. We want to prove that
$\mathsf {D}_{t}^{\left [ i\right ] }=\{T,F\}$
. We want to prove that
 $\{T,F\}=\{\Phi (\varphi )\mid \varphi \in \mathsf {CME}_{t}\cap \mathsf {RIGIDS }\text { and }\Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\varphi ))\}$
. On the one hand,
$\{T,F\}=\{\Phi (\varphi )\mid \varphi \in \mathsf {CME}_{t}\cap \mathsf {RIGIDS }\text { and }\Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\varphi ))\}$
. On the one hand,
 $\{\Phi (\varphi )\mid \varphi \in \mathsf {CME}_{t}\cap \mathsf {RIGIDS}\text { and }\Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\varphi ))\}\subseteq \{T,F\}$
, by definition of
$\{\Phi (\varphi )\mid \varphi \in \mathsf {CME}_{t}\cap \mathsf {RIGIDS}\text { and }\Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\varphi ))\}\subseteq \{T,F\}$
, by definition of
 $\Phi $
. Also, we have already seen that
$\Phi $
. Also, we have already seen that
 $\Phi (\bot )=F$
and
$\Phi (\bot )=F$
and
 $\Phi (\top )=T$
. Moreover,
$\Phi (\top )=T$
. Moreover,
 $\vdash @_{i}(\mathsf {EXISTS}(\varphi ))$
, as
$\vdash @_{i}(\mathsf {EXISTS}(\varphi ))$
, as
 $(\varphi \equiv \top )\vee (\varphi \equiv \bot )$
is a tautology and we can use Rule Gen
$(\varphi \equiv \top )\vee (\varphi \equiv \bot )$
is a tautology and we can use Rule Gen
 $_{@}$
. In particular,
$_{@}$
. In particular,
 $\vdash @_{i}( \mathsf {EXISTS}(\bot ))$
and
$\vdash @_{i}( \mathsf {EXISTS}(\bot ))$
and
 $\vdash @_{i}(\mathsf {EXISTS}(\top ))$
. Thus we have the reverse inclusion as well.
$\vdash @_{i}(\mathsf {EXISTS}(\top ))$
. Thus we have the reverse inclusion as well. -
(5) That
 $\mathsf {D}_{t}=\{T,F\}=\bigcup \limits _{[i]\in W}\mathsf {D} _{t}^{[i]}$
is now clear.
$\mathsf {D}_{t}=\{T,F\}=\bigcup \limits _{[i]\in W}\mathsf {D} _{t}^{[i]}$
is now clear. -
(6) Condition (6) is immediate as, by consistency,
 $\Gamma ^{\ast }\not \vdash \bot $
and so
$\Gamma ^{\ast }\not \vdash \bot $
and so
 $\Phi (\bot )=F$
.
$\Phi (\bot )=F$
.
Next we go through the same process for type e.
Definition 9.6 (Type e).
We define
![]() $\Phi $
,
$\Phi $
,
![]() $\mathsf {D}_{e}$
, and
$\mathsf {D}_{e}$
, and
![]() $\mathsf {D}_{e}^{\left [ i\right ] }$
as follows:
$\mathsf {D}_{e}^{\left [ i\right ] }$
as follows:
 $$ \begin{align*} \Phi (\alpha _{e})= \begin{cases} \begin{array}{ll} \{\beta _{e}\mid \beta _{e}\in \mathsf{CME}_{e}\cap \mathsf{RIGIDS}\text{ and }\Gamma ^{\ast }\vdash \alpha _{e}\equiv \beta _{e}\}, & \text{ if }\Gamma ^{\ast }\vdash \mathsf{DEN}(\alpha _{e}), \\ \mathsf{\divideontimes }, & \text{ otherwise}. \end{array} \end{cases} \end{align*} $$
$$ \begin{align*} \Phi (\alpha _{e})= \begin{cases} \begin{array}{ll} \{\beta _{e}\mid \beta _{e}\in \mathsf{CME}_{e}\cap \mathsf{RIGIDS}\text{ and }\Gamma ^{\ast }\vdash \alpha _{e}\equiv \beta _{e}\}, & \text{ if }\Gamma ^{\ast }\vdash \mathsf{DEN}(\alpha _{e}), \\ \mathsf{\divideontimes }, & \text{ otherwise}. \end{array} \end{cases} \end{align*} $$
-
•
 $\mathsf {D}_e=\{\Phi (\alpha _e)\mid \alpha _e\in \mathsf {CME}_e\cap \mathsf {RIGIDS}$
and
$\mathsf {D}_e=\{\Phi (\alpha _e)\mid \alpha _e\in \mathsf {CME}_e\cap \mathsf {RIGIDS}$
and
 $\Gamma ^\ast \vdash \mathsf {DEN}(\alpha _e)\}$
.
$\Gamma ^\ast \vdash \mathsf {DEN}(\alpha _e)\}$
. -
•
 $\mathsf {D}_{e}^{[i]}=\{ \Phi (\alpha _{e})\mid \alpha _{e}\in \mathsf {CME}_{e}\cap \mathsf {RIGIDS}$
and
$\mathsf {D}_{e}^{[i]}=\{ \Phi (\alpha _{e})\mid \alpha _{e}\in \mathsf {CME}_{e}\cap \mathsf {RIGIDS}$
and
 $\Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\alpha _{e}))\}$
.
$\Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\alpha _{e}))\}$
.
Proposition 9.7 (Type e).
Let
![]() $\Phi $
,
$\Phi $
,
![]() $\mathsf {D}_{e}$
, and
$\mathsf {D}_{e}$
, and
![]() $\mathsf {D}_{e}^{[i]}$
be as just defined. Then the six conditions in Figure 2 hold.
$\mathsf {D}_{e}^{[i]}$
be as just defined. Then the six conditions in Figure 2 hold.
Proof We establish these conditions as follows:
-
(1) Immediate: the definition of
 $\mathsf {D}_e$
simply restates the first condition.
$\mathsf {D}_e$
simply restates the first condition. -
(2) If
 $\Gamma ^\ast \vdash \lnot \mathsf {DEN}(\alpha _e)$
then by consistency
$\Gamma ^\ast \vdash \lnot \mathsf {DEN}(\alpha _e)$
then by consistency
 $\Gamma ^\ast \not \vdash \mathsf {DEN}(\alpha _e)$
and so
$\Gamma ^\ast \not \vdash \mathsf {DEN}(\alpha _e)$
and so
 $\Phi (\alpha _e)=\mathsf {\divideontimes }$
. If
$\Phi (\alpha _e)=\mathsf {\divideontimes }$
. If
 $\Phi (\alpha _e)= \mathsf {\divideontimes }$
then
$\Phi (\alpha _e)= \mathsf {\divideontimes }$
then
 $\Gamma ^\ast \vdash \lnot \mathsf {DEN}(\alpha _e)$
.
$\Gamma ^\ast \vdash \lnot \mathsf {DEN}(\alpha _e)$
. -
(3) Let
 $\alpha _{e}$
,
$\alpha _{e}$
,
 $\delta _{e}\in \mathsf {CME}_{e}\cap \mathsf {RIGIDS}$
such that
$\delta _{e}\in \mathsf {CME}_{e}\cap \mathsf {RIGIDS}$
such that
 $\Gamma ^{\ast }\vdash \mathsf {DEN}(\alpha _{e})$
and
$\Gamma ^{\ast }\vdash \mathsf {DEN}(\alpha _{e})$
and
 $\Gamma ^{\ast }\vdash \mathsf {DEN}(\delta _{e})$
. Then,
$\Gamma ^{\ast }\vdash \mathsf {DEN}(\delta _{e})$
. Then,
 $\Phi (\alpha _{e}) =\{\beta _{e}\mid \beta _{e}\in \mathsf {CME}_{e}\cap \mathsf {RIGIDS}$
and
$\Phi (\alpha _{e}) =\{\beta _{e}\mid \beta _{e}\in \mathsf {CME}_{e}\cap \mathsf {RIGIDS}$
and
 $\Gamma ^{\ast }\vdash \alpha _{e}\equiv \beta _{e}\},\ \text {and}$
$\Gamma ^{\ast }\vdash \alpha _{e}\equiv \beta _{e}\},\ \text {and}$
 $\Phi (\delta _{e}) =\{\beta _{e}\mid \beta _{e}\in \mathsf {CME}_{e}\cap \mathsf {RIGIDS}\text { and }\Gamma ^{\ast }\vdash \delta _{e}\equiv \beta _{e}\}$
. If
$\Phi (\delta _{e}) =\{\beta _{e}\mid \beta _{e}\in \mathsf {CME}_{e}\cap \mathsf {RIGIDS}\text { and }\Gamma ^{\ast }\vdash \delta _{e}\equiv \beta _{e}\}$
. If
 $\Phi (\alpha _{e})=\Phi (\delta _{e})$
then
$\Phi (\alpha _{e})=\Phi (\delta _{e})$
then
 $\Gamma ^{\ast }\vdash \alpha _{e}\equiv \delta _{e}$
, using Equality Schemas (Axioms 4) for
$\Gamma ^{\ast }\vdash \alpha _{e}\equiv \delta _{e}$
, using Equality Schemas (Axioms 4) for
 $\simeq $
and the fact that
$\simeq $
and the fact that
 $\Gamma ^{\ast }\vdash \mathsf {DEN}(\alpha _{e})$
and
$\Gamma ^{\ast }\vdash \mathsf {DEN}(\alpha _{e})$
and
 $\Gamma ^{\ast }\vdash \mathsf {DEN}(\delta _{e})$
that allow us to use
$\Gamma ^{\ast }\vdash \mathsf {DEN}(\delta _{e})$
that allow us to use
 $\equiv $
instead of
$\equiv $
instead of
 $\simeq $
(by applying Proposition 6.3(1b)). The other direction,
$\simeq $
(by applying Proposition 6.3(1b)). The other direction,
 $\Gamma ^{\ast }\vdash \alpha _{e}\equiv \delta _{e}$
implies
$\Gamma ^{\ast }\vdash \alpha _{e}\equiv \delta _{e}$
implies
 $\Phi (\alpha _{e})=\Phi (\delta _{e})$
, is obvious (by the same reasons as above).
$\Phi (\alpha _{e})=\Phi (\delta _{e})$
, is obvious (by the same reasons as above). -
(4) We define
 $\mathsf {D}_{e}^{[i]}=\{\Phi (\alpha _{e})\mid \alpha _{e}\in \mathsf {CME} _{e}\cap \mathsf {RIGIDS}\text { and }\Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\alpha _{e}))\}$
. This set is not empty because for every
$\mathsf {D}_{e}^{[i]}=\{\Phi (\alpha _{e})\mid \alpha _{e}\in \mathsf {CME} _{e}\cap \mathsf {RIGIDS}\text { and }\Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\alpha _{e}))\}$
. This set is not empty because for every
 $v_{e}\in \mathsf {VAR}_{e}$
,
$v_{e}\in \mathsf {VAR}_{e}$
,
 $ \vdash \exists v_{e}\top $
(Axiom 2a) and then, using the Gen
$ \vdash \exists v_{e}\top $
(Axiom 2a) and then, using the Gen
 $_{@}$
Rule, we have that
$_{@}$
Rule, we have that
 $@_{i}\exists v_{e}\top \in \Gamma ^{\ast }$
as well. As
$@_{i}\exists v_{e}\top \in \Gamma ^{\ast }$
as well. As
 $\Gamma ^{\ast }$
is
$\Gamma ^{\ast }$
is
 $\exists $
-saturated, there is a constant
$\exists $
-saturated, there is a constant
 $ c_{e}$
such that
$ c_{e}$
such that
 $@_{i}(\mathsf {EXISTS}(c_{e}))\in \Gamma ^{\ast }$
. Thus,
$@_{i}(\mathsf {EXISTS}(c_{e}))\in \Gamma ^{\ast }$
. Thus,
 $\Phi (c_{e})\in \mathsf {D}_{e}^{[i]}$
. As
$\Phi (c_{e})\in \mathsf {D}_{e}^{[i]}$
. As
 $\vdash @_{i}(\mathsf {EXISTS }(c_{e})\equiv @_{i}\mathsf {EXISTS}(@_{i}c_{e}))$
(by Axiom 5b and Proposition 6.3(1b)) we obtain
$\vdash @_{i}(\mathsf {EXISTS }(c_{e})\equiv @_{i}\mathsf {EXISTS}(@_{i}c_{e}))$
(by Axiom 5b and Proposition 6.3(1b)) we obtain
 $@_{i}(\mathsf {EXISTS}(@_{i}c_{e}))\in \Gamma ^{\ast }$
and then we have
$@_{i}(\mathsf {EXISTS}(@_{i}c_{e}))\in \Gamma ^{\ast }$
and then we have
 $\Phi (@_{i}c_{e})\in \mathsf {D}_{e}^{[i]}$
because
$\Phi (@_{i}c_{e})\in \mathsf {D}_{e}^{[i]}$
because
 $ @_{i}c_{e}\in \mathsf {CME}_{e}\cap \mathsf {RIGIDS}$
.
$ @_{i}c_{e}\in \mathsf {CME}_{e}\cap \mathsf {RIGIDS}$
. -
(5) Suppose that
 $\Phi (\alpha _{e})\in \mathsf {D}_{e}$
. Note that this means that
$\Phi (\alpha _{e})\in \mathsf {D}_{e}$
. Note that this means that
 $\alpha _{e} \in \mathsf {RIGIDS}$
. Hence from the fact that
$\alpha _{e} \in \mathsf {RIGIDS}$
. Hence from the fact that
 $\Gamma ^{\ast }\vdash \mathsf {DEN}(\alpha _{e})$
, and Proposition 6.3(3a) we have
$\Gamma ^{\ast }\vdash \mathsf {DEN}(\alpha _{e})$
, and Proposition 6.3(3a) we have
 $\Gamma ^{\ast }\vdash \mathsf {E(EXISTS} (\alpha _{e})$
. Hence by the
$\Gamma ^{\ast }\vdash \mathsf {E(EXISTS} (\alpha _{e})$
. Hence by the
 $\mathsf {E}$
-saturation of
$\mathsf {E}$
-saturation of
 $\Gamma ^{\ast }$
, there is a nominal i such that
$\Gamma ^{\ast }$
, there is a nominal i such that
 $\Gamma ^{\ast }\vdash @_{i}\mathsf {(EXISTS} (\alpha _{e}))$
. So
$\Gamma ^{\ast }\vdash @_{i}\mathsf {(EXISTS} (\alpha _{e}))$
. So
 $\Phi (\alpha _{e})\in \mathsf {D}_{e}^{\left [ i\right ] }$
. The reverse inclusion follows using
$\Phi (\alpha _{e})\in \mathsf {D}_{e}^{\left [ i\right ] }$
. The reverse inclusion follows using
 $\vdash @_{i}(\mathsf {EXISTS}(\alpha _{a}))\rightarrow \mathsf {DEN}(\alpha _{a})$
(it follows easily from Axiom 9b, Rule Gen
$\vdash @_{i}(\mathsf {EXISTS}(\alpha _{a}))\rightarrow \mathsf {DEN}(\alpha _{a})$
(it follows easily from Axiom 9b, Rule Gen
 $_{@}$
, Distributivity Axiom 1c, Proposition 6.3(1c), and previous Proposition 6.3(1e)). Thus, we have shown that
$_{@}$
, Distributivity Axiom 1c, Proposition 6.3(1c), and previous Proposition 6.3(1e)). Thus, we have shown that
 $\mathsf {D}_{e}=_{\ }\bigcup \limits _{i\in \mathsf {NOM}}\mathsf {D}_{e}^{\left [ i\right ]}$
.
$\mathsf {D}_{e}=_{\ }\bigcup \limits _{i\in \mathsf {NOM}}\mathsf {D}_{e}^{\left [ i\right ]}$
.
We now turn to the inductive step, driving through the same type of argument for the function types. We first give definitions of
![]() $\Phi $
,
$\Phi $
,
![]() $\mathsf {D} _{ab}$
, and
$\mathsf {D} _{ab}$
, and
![]() $\mathsf {D}_{ab}^{[i]}$
for a function type
$\mathsf {D}_{ab}^{[i]}$
for a function type
![]() $\left \langle a,b\right \rangle $
of kind e, and then prove two propositions showing that the definitions work the way we want.
$\left \langle a,b\right \rangle $
of kind e, and then prove two propositions showing that the definitions work the way we want.
Definition 9.8 (
 $\Phi $
,
$\Phi $
,
 $\mathsf {D}_{ab}$
, and
$\mathsf {D}_{ab}$
, and
 $\mathsf {D}_{ab}^{\left [ i \right ] }$
for kind e).
$\mathsf {D}_{ab}^{\left [ i \right ] }$
for kind e).
Let
![]() $\langle a,b\rangle \in \mathsf {KIND}_{e}$
. Assume that
$\langle a,b\rangle \in \mathsf {KIND}_{e}$
. Assume that
![]() $\mathsf {D}_{a}$
and
$\mathsf {D}_{a}$
and
![]() $\mathsf {D}_{b}$
have been defined; note that this means that
$\mathsf {D}_{b}$
have been defined; note that this means that
![]() $\Phi (\alpha _{a})$
and
$\Phi (\alpha _{a})$
and
![]() $\Phi (\alpha _{b})$
are defined, for all closed expressions
$\Phi (\alpha _{b})$
are defined, for all closed expressions
![]() $\alpha $
of types a and b respectively. Furthermore, assume that the six conditions in Figure 2 hold for types a and b. Then we define:
$\alpha $
of types a and b respectively. Furthermore, assume that the six conditions in Figure 2 hold for types a and b. Then we define:
-
• Let
 $\gamma _{ab}\in \mathsf {CME}_{ab}$
. If
$\gamma _{ab}\in \mathsf {CME}_{ab}$
. If
 $\Gamma ^{\ast }\not \vdash \mathsf {DEN}(\gamma _{ab})$
then we set
$\Gamma ^{\ast }\not \vdash \mathsf {DEN}(\gamma _{ab})$
then we set
 $\Phi (\gamma _{ab})$
as
$\Phi (\gamma _{ab})$
as
 $ \divideontimes $
. On the other hand, if
$ \divideontimes $
. On the other hand, if
 $\Gamma ^{\ast }\vdash \mathsf {DEN}(\gamma _{ab})$
, then
$\Gamma ^{\ast }\vdash \mathsf {DEN}(\gamma _{ab})$
, then
 $\Phi (\gamma _{ab})$
will be the partial function where
$\Phi (\gamma _{ab})$
will be the partial function where $$ \begin{align*} \begin{array}{llll} \Phi (\gamma _{ab}): & \mathsf{D}_{a} & \rightsquigarrow &\mathsf{D}_{b} \\ &\Phi (\alpha _{a}) &\mapsto &\Phi (@_{i_{n}}\gamma _{ab}\alpha_{a}), \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{llll} \Phi (\gamma _{ab}): & \mathsf{D}_{a} & \rightsquigarrow &\mathsf{D}_{b} \\ &\Phi (\alpha _{a}) &\mapsto &\Phi (@_{i_{n}}\gamma _{ab}\alpha_{a}), \end{array} \end{align*} $$
 $i_{n}$
is the nominal with least n such that
$i_{n}$
is the nominal with least n such that
 $i_{n}\in \Gamma ^{\ast }$
(since
$i_{n}\in \Gamma ^{\ast }$
(since
 $\Gamma ^{\ast }$
is named, it contains at least one nominal).
$\Gamma ^{\ast }$
is named, it contains at least one nominal).
The partial function
 $\Phi (\gamma _{ab})$
is defined as follows:
$\Phi (\gamma _{ab})$
is defined as follows:-
– if
 $\Gamma ^{\ast }\vdash \mathsf {DEN}(@_{i_{n}}\gamma _{ab}\alpha _{a})$
then
$\Gamma ^{\ast }\vdash \mathsf {DEN}(@_{i_{n}}\gamma _{ab}\alpha _{a})$
then
 $\Phi (@_{i_{n}}\gamma _{ab}\alpha _{a})\in \mathsf {D}_{b}$
, and
$\Phi (@_{i_{n}}\gamma _{ab}\alpha _{a})\in \mathsf {D}_{b}$
, and -
– if
 $\Gamma ^{\ast }\not \vdash \mathsf {DEN}(@_{i_{n}}\gamma _{ab}\alpha _{a})$
then
$\Gamma ^{\ast }\not \vdash \mathsf {DEN}(@_{i_{n}}\gamma _{ab}\alpha _{a})$
then
 $\Phi (@_{i_{n}}\gamma _{ab}\alpha _{a})=\divideontimes $
.
$\Phi (@_{i_{n}}\gamma _{ab}\alpha _{a})=\divideontimes $
.
-
-
• Define
 $\mathsf {D}_{ab}=\left \{ \Phi (\gamma _{ab})\mid \gamma _{ab}\in \mathsf {CME}_{ab}\cap \mathsf {RIGIDS}\text { and }\Gamma ^{\ast }\vdash \mathsf {DEN}(\gamma _{ab})\right \} $
.
$\mathsf {D}_{ab}=\left \{ \Phi (\gamma _{ab})\mid \gamma _{ab}\in \mathsf {CME}_{ab}\cap \mathsf {RIGIDS}\text { and }\Gamma ^{\ast }\vdash \mathsf {DEN}(\gamma _{ab})\right \} $
. -
• Define
 $\mathsf {D}_{ab}^{\left [ i\right ] }=\left \{ \Phi (\gamma _{ab})\mid \gamma _{ab}\in \mathsf {CME}_{ab}\cap \mathsf {RIGIDS}\text { and }\Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\gamma _{ab}))\right \} $
.
$\mathsf {D}_{ab}^{\left [ i\right ] }=\left \{ \Phi (\gamma _{ab})\mid \gamma _{ab}\in \mathsf {CME}_{ab}\cap \mathsf {RIGIDS}\text { and }\Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\gamma _{ab}))\right \} $
.
Proposition 9.9 (Kind e).
Let
![]() $\Phi $
be as just defined, and let
$\Phi $
be as just defined, and let
![]() $\Phi (\alpha _a),\Phi (\beta _a)\in \mathsf {D}_a$
such that
$\Phi (\alpha _a),\Phi (\beta _a)\in \mathsf {D}_a$
such that
![]() $\Phi (\alpha _a)=\Phi (\beta _a)$
. Then
$\Phi (\alpha _a)=\Phi (\beta _a)$
. Then
![]() $\Phi (@_{i_{n}}\gamma _{ab}\alpha _a)=\Phi (@_{i_{n}}\gamma _{ab}\beta _a)$
.
$\Phi (@_{i_{n}}\gamma _{ab}\alpha _a)=\Phi (@_{i_{n}}\gamma _{ab}\beta _a)$
.
Proof Let
![]() $\Phi (\alpha _{a}),\Phi (\beta _{a})\in \mathsf {D}_{a}$
, and
$\Phi (\alpha _{a}),\Phi (\beta _{a})\in \mathsf {D}_{a}$
, and
![]() $\Phi (\alpha _{a})=\Phi (\beta _{a})$
. By the induction hypothesis on type a, as
$\Phi (\alpha _{a})=\Phi (\beta _{a})$
. By the induction hypothesis on type a, as
![]() $\Gamma ^{\ast }\vdash \mathsf {DEN}(\alpha _{a})$
and
$\Gamma ^{\ast }\vdash \mathsf {DEN}(\alpha _{a})$
and
![]() $\Gamma ^{\ast }\vdash \mathsf {DEN}(\beta _{a})$
, we have that
$\Gamma ^{\ast }\vdash \mathsf {DEN}(\beta _{a})$
, we have that
![]() $\Gamma ^{\ast }\vdash \alpha _{a}\equiv \beta _{a}$
, and so
$\Gamma ^{\ast }\vdash \alpha _{a}\equiv \beta _{a}$
, and so
![]() $\Gamma ^{\ast }\vdash \alpha _{a}\simeq \beta _{a}$
, by definition of
$\Gamma ^{\ast }\vdash \alpha _{a}\simeq \beta _{a}$
, by definition of
![]() $\simeq $
. Then
$\simeq $
. Then
![]() $\Gamma ^{\ast }\vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\simeq @_{i_{n}}\gamma _{ab}\beta _{a}$
, by Axiom 11a and maximal consistency.
$\Gamma ^{\ast }\vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\simeq @_{i_{n}}\gamma _{ab}\beta _{a}$
, by Axiom 11a and maximal consistency.
We now have two cases: (i)
![]() $\Gamma ^{\ast }\vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\equiv @_{i_{n}}\gamma _{ab}\beta _{a}$
or (ii)
$\Gamma ^{\ast }\vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\equiv @_{i_{n}}\gamma _{ab}\beta _{a}$
or (ii)
![]() $\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(@_{i_{n}}\gamma _{ab}\alpha _{a})$
and
$\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(@_{i_{n}}\gamma _{ab}\alpha _{a})$
and
![]() $\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(@_{i_{n}}\gamma _{ab}\beta _{a})$
. Either way, we have that
$\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(@_{i_{n}}\gamma _{ab}\beta _{a})$
. Either way, we have that
![]() $\Phi (@_{i_{n}}\gamma _{ab}\alpha _{a})=\Phi (@_{i_{n}}\gamma _{ab}\beta _{a})$
, by the induction hypothesis on type b (conditions (3) and (2) from Figure 2).
$\Phi (@_{i_{n}}\gamma _{ab}\alpha _{a})=\Phi (@_{i_{n}}\gamma _{ab}\beta _{a})$
, by the induction hypothesis on type b (conditions (3) and (2) from Figure 2).
Proposition 9.10 (Kind e).
Let
![]() $\Phi $
,
$\Phi $
,
![]() $\mathsf {D}_{ab}$
, and
$\mathsf {D}_{ab}$
, and
![]() $\mathsf {D} _{ab}^{\left [ i\right ] }$
be as given in Definition 9.8. Then the six conditions in Figure 2 are satisfied.
$\mathsf {D} _{ab}^{\left [ i\right ] }$
be as given in Definition 9.8. Then the six conditions in Figure 2 are satisfied.
Proof We establish these conditions as follows:
-
(1) By definition
 $\mathsf {D}_{ab}=\left \{ \Phi (\gamma _{ab})\mid \gamma _{ab}\in \mathsf {CME}_{ab}\cap \mathsf {RIGIDS} \text { and } \Gamma ^\ast \vdash \mathsf {DEN}(\gamma _{ab})\right \}$
.
$\mathsf {D}_{ab}=\left \{ \Phi (\gamma _{ab})\mid \gamma _{ab}\in \mathsf {CME}_{ab}\cap \mathsf {RIGIDS} \text { and } \Gamma ^\ast \vdash \mathsf {DEN}(\gamma _{ab})\right \}$
. -
(2) By definition of
 $\Phi $
,
$\Phi $
,
 $\Phi (\gamma _{ab})=\mathsf {\ \divideontimes }$
iff
$\Phi (\gamma _{ab})=\mathsf {\ \divideontimes }$
iff
 $\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(\gamma _{ab})$
.
$\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(\gamma _{ab})$
. -
(4)
 $\mathsf {D}_{ab}^{\left [ i\right ] }=\left \{ \Phi (\gamma _{ab})\mid \gamma _{ab}\in \mathsf {CME}_{b}\cap \mathsf {RIGIDS}\text { and }\Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\gamma _{ab}))\right \} $
by definition. We need to show that each local domain is non-empty. By the induction hypothesis,
$\mathsf {D}_{ab}^{\left [ i\right ] }=\left \{ \Phi (\gamma _{ab})\mid \gamma _{ab}\in \mathsf {CME}_{b}\cap \mathsf {RIGIDS}\text { and }\Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\gamma _{ab}))\right \} $
by definition. We need to show that each local domain is non-empty. By the induction hypothesis,
 $\mathsf {D}_{b}\not =\varnothing $
, and so there is
$\mathsf {D}_{b}\not =\varnothing $
, and so there is
 $\Phi (\beta _{b})\in \mathsf {D}_{b}$
with
$\Phi (\beta _{b})\in \mathsf {D}_{b}$
with
 $\beta _{b}\in \mathsf {CME}_{b}\cap \mathsf {RIGIDS}$
and
$\beta _{b}\in \mathsf {CME}_{b}\cap \mathsf {RIGIDS}$
and
 $\Gamma ^{\ast }\vdash \mathsf {DEN}(\beta _{b})$
. By the induction hypothesis,
$\Gamma ^{\ast }\vdash \mathsf {DEN}(\beta _{b})$
. By the induction hypothesis,
 $\mathsf {D}_{b}^{\left [ i\right ]}\not =\varnothing $
, and so there is
$\mathsf {D}_{b}^{\left [ i\right ]}\not =\varnothing $
, and so there is
 $\Phi (\beta _{b})\in \mathsf {D}_{b}$
with
$\Phi (\beta _{b})\in \mathsf {D}_{b}$
with
 $\beta _{b}\in \mathsf {CME}_{b}\cap \mathsf {RIGIDS}$
and
$\beta _{b}\in \mathsf {CME}_{b}\cap \mathsf {RIGIDS}$
and
 $\Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\beta _{b}))$
. From the Comprehension axiom (9a) and the Rule Gen
$\Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\beta _{b}))$
. From the Comprehension axiom (9a) and the Rule Gen
 $_{@}$
, we have that
$_{@}$
, we have that
 $\vdash @_{i}(\mathsf {EXISTS}\left \langle \lambda x_{a}\beta _{b}\right \rangle )$
and so
$\vdash @_{i}(\mathsf {EXISTS}\left \langle \lambda x_{a}\beta _{b}\right \rangle )$
and so
 $\Gamma ^{\ast }\vdash @_{i}(\mathsf { EXISTS}@_{i}\left \langle \lambda x_{a}\beta _{b}\right \rangle )$
, as
$\Gamma ^{\ast }\vdash @_{i}(\mathsf { EXISTS}@_{i}\left \langle \lambda x_{a}\beta _{b}\right \rangle )$
, as
 $\vdash @_{i}(\mathsf {EXISTS}\left \langle \lambda x_{a}\beta _{b}\right \rangle ) \ \equiv @_{i}(\mathsf {EXISTS}@_{i}\left \langle \lambda x_{a}\beta _{b}\right \rangle )$
(by Axiom 5b and Proposition 6.3(1b)) and maximal consistency. Therefore,
$\vdash @_{i}(\mathsf {EXISTS}\left \langle \lambda x_{a}\beta _{b}\right \rangle ) \ \equiv @_{i}(\mathsf {EXISTS}@_{i}\left \langle \lambda x_{a}\beta _{b}\right \rangle )$
(by Axiom 5b and Proposition 6.3(1b)) and maximal consistency. Therefore,
 $\Phi (@_{i}\left \langle \lambda x_{a}\beta _{b}\right \rangle )\in \mathsf {D}_{ab}^{\left [ i\right ] }$
, as required.
$\Phi (@_{i}\left \langle \lambda x_{a}\beta _{b}\right \rangle )\in \mathsf {D}_{ab}^{\left [ i\right ] }$
, as required. -
(5) We want to prove that
 $\mathsf {D}_{ab}=\displaystyle \bigcup \limits _{[i]\in W}\mathsf {D}_{ab}^{[i]}$
. First, any element of
$\mathsf {D}_{ab}=\displaystyle \bigcup \limits _{[i]\in W}\mathsf {D}_{ab}^{[i]}$
. First, any element of
 $\mathsf {D}_{ab}$
is of the form
$\mathsf {D}_{ab}$
is of the form
 $\Phi (\gamma _{ab})\in \mathsf {D}_{ab}$
with
$\Phi (\gamma _{ab})\in \mathsf {D}_{ab}$
with
 $\Gamma ^{\ast }\vdash \mathsf {DEN} (\gamma _{ab})$
and
$\Gamma ^{\ast }\vdash \mathsf {DEN} (\gamma _{ab})$
and
 $\gamma _{ab}\in \mathsf {CME}_{b}\cap \mathsf {RIGIDS}$
. By Proposition 6.3(3a) it follows that
$\gamma _{ab}\in \mathsf {CME}_{b}\cap \mathsf {RIGIDS}$
. By Proposition 6.3(3a) it follows that
 $\Gamma ^{\ast }\vdash \mathsf {E(EXISTS}(\gamma _{ab}))$
. Hence, by
$\Gamma ^{\ast }\vdash \mathsf {E(EXISTS}(\gamma _{ab}))$
. Hence, by
 $\mathsf {E}$
-saturation, there is a nominal i such that
$\mathsf {E}$
-saturation, there is a nominal i such that
 $@_{i}\mathsf {(EXISTS}(\gamma _{ab}))\in \Gamma ^{\ast }$
. Therefore,
$@_{i}\mathsf {(EXISTS}(\gamma _{ab}))\in \Gamma ^{\ast }$
. Therefore,
 $\Phi (\gamma _{ab})\in \mathsf {D}_{ab}^{[i]}$
. To prove the converse, use the logical theorem
$\Phi (\gamma _{ab})\in \mathsf {D}_{ab}^{[i]}$
. To prove the converse, use the logical theorem
 $@_{i}\mathsf {(EXIST}(\gamma _{ab}))\rightarrow \mathsf {DEN}(\gamma _{ab})$
. The proof of this theorem uses the same axioms and rules already applied in Proposition 9.7(5).
$@_{i}\mathsf {(EXIST}(\gamma _{ab}))\rightarrow \mathsf {DEN}(\gamma _{ab})$
. The proof of this theorem uses the same axioms and rules already applied in Proposition 9.7(5). -
(3) Let
 $\gamma _{ab}$
,
$\gamma _{ab}$
,
 $\delta _{ab}\in \mathsf {CME}_{ab}\cap \mathsf {RIGIDS}$
such that
$\delta _{ab}\in \mathsf {CME}_{ab}\cap \mathsf {RIGIDS}$
such that
 $\Gamma ^{\ast }\vdash \mathsf {DEN}(\gamma _{ab})$
and
$\Gamma ^{\ast }\vdash \mathsf {DEN}(\gamma _{ab})$
and
 $\Gamma ^{\ast }\vdash \mathsf {DEN}(\delta _{ab})$
. We want to show that
$\Gamma ^{\ast }\vdash \mathsf {DEN}(\delta _{ab})$
. We want to show that
 $\Phi (\gamma _{ab})=\Phi (\delta _{ab})$
iff
$\Phi (\gamma _{ab})=\Phi (\delta _{ab})$
iff
 $\Gamma ^{\ast }\vdash \gamma _{ab}\equiv \delta _{ab}$
.
$\Gamma ^{\ast }\vdash \gamma _{ab}\equiv \delta _{ab}$
.(
 $\Rightarrow $
) Suppose that
$\Rightarrow $
) Suppose that
 $\Phi (\gamma _{ab})=\Phi (\delta _{ab})$
. From conditions (4) and (5) in Figure 2, we have
$\Phi (\gamma _{ab})=\Phi (\delta _{ab})$
. From conditions (4) and (5) in Figure 2, we have
 $\Phi (\gamma _{ab}),\Phi (\delta _{ab})\in \mathsf {D}_{ab}^{[i]}$
for some nominal i. Thus the following two statements are true: (1)
$\Phi (\gamma _{ab}),\Phi (\delta _{ab})\in \mathsf {D}_{ab}^{[i]}$
for some nominal i. Thus the following two statements are true: (1)
 $\Gamma ^{\ast }\vdash @_{i}( \mathsf {EXISTS}(\gamma _{ab}))$
and (2)
$\Gamma ^{\ast }\vdash @_{i}( \mathsf {EXISTS}(\gamma _{ab}))$
and (2)
 $\Gamma ^{\ast }\vdash @_{i}( \mathsf {EXISTS}(\delta _{ab}))$
. Furthermore, using Extensionality (Axiom 12), the Gen
$\Gamma ^{\ast }\vdash @_{i}( \mathsf {EXISTS}(\delta _{ab}))$
. Furthermore, using Extensionality (Axiom 12), the Gen
 $_{@}$
Rule, and Axiom 1c we can prove that
$_{@}$
Rule, and Axiom 1c we can prove that
 $(@_{i}(\mathsf {EXISTS}(\gamma _{ab}))\wedge @_{i}(\mathsf {\ EXISTS}(\delta _{ab})))\rightarrow (@_{i}\forall x_{a}\left ( \gamma _{ab}x_{a}\simeq \delta _{ab}x_{a}\right ) \rightarrow @_{i}(\gamma _{ab}\equiv \delta _{ab}))$
is a theorem. Therefore,
$(@_{i}(\mathsf {EXISTS}(\gamma _{ab}))\wedge @_{i}(\mathsf {\ EXISTS}(\delta _{ab})))\rightarrow (@_{i}\forall x_{a}\left ( \gamma _{ab}x_{a}\simeq \delta _{ab}x_{a}\right ) \rightarrow @_{i}(\gamma _{ab}\equiv \delta _{ab}))$
is a theorem. Therefore,
 $\Gamma ^{\ast }\vdash (@_{i}\forall x_{a}\left ( \gamma _{ab}x_{a}\simeq \delta _{ab}x_{a}\right ) \rightarrow @_{i}(\gamma _{ab}\equiv \delta _{ab}))$
.
$\Gamma ^{\ast }\vdash (@_{i}\forall x_{a}\left ( \gamma _{ab}x_{a}\simeq \delta _{ab}x_{a}\right ) \rightarrow @_{i}(\gamma _{ab}\equiv \delta _{ab}))$
.So let us suppose for the sake of contradiction that
 $\Gamma ^{\ast }\not \vdash \gamma _{ab}\equiv \delta _{ab}$
. Since
$\Gamma ^{\ast }\not \vdash \gamma _{ab}\equiv \delta _{ab}$
. Since
 $\gamma _{ab}$
,
$\gamma _{ab}$
,
 $\delta _{ab}\in \mathsf {RIGIDS}$
,
$\delta _{ab}\in \mathsf {RIGIDS}$
,
 $\Gamma ^{\ast }\not \vdash @_{i}(\gamma _{ab}\equiv \delta _{ab})$
(by Equality schemas, Axioms 3d and 5a, and Proposition 6.3(1b)) and so we have
$\Gamma ^{\ast }\not \vdash @_{i}(\gamma _{ab}\equiv \delta _{ab})$
(by Equality schemas, Axioms 3d and 5a, and Proposition 6.3(1b)) and so we have
 $\Gamma ^{\ast }\vdash \lnot @_{i}\forall x_{a}(\gamma _{ab}x_{a}\simeq \delta _{ab}x_{a})$
. Hence, using Axiom 3b we have that
$\Gamma ^{\ast }\vdash \lnot @_{i}\forall x_{a}(\gamma _{ab}x_{a}\simeq \delta _{ab}x_{a})$
. Hence, using Axiom 3b we have that
 $\Gamma ^{\ast }\vdash @_{i}\exists x_{a}\lnot (\gamma _{ab}x_{a}\simeq \delta _{ab}x_{a})$
. So by existential saturation there is a constant
$\Gamma ^{\ast }\vdash @_{i}\exists x_{a}\lnot (\gamma _{ab}x_{a}\simeq \delta _{ab}x_{a})$
. So by existential saturation there is a constant
 $c_{a}$
such that
$c_{a}$
such that
 $@_{i}(\mathsf { \ EXISTS}(c_{a}))\in \Gamma ^{\ast }$
and
$@_{i}(\mathsf { \ EXISTS}(c_{a}))\in \Gamma ^{\ast }$
and
 $\Gamma ^{\ast }\vdash @_{i}\lnot (\gamma _{ab}@_{i}c_{a}\simeq \delta _{ab}@_{i}c_{a})$
. Now, by using Proposition 6.3(2f) as well as the functional schemas (11a and 11b) and Axiom 3d, we obtain
$\Gamma ^{\ast }\vdash @_{i}\lnot (\gamma _{ab}@_{i}c_{a}\simeq \delta _{ab}@_{i}c_{a})$
. Now, by using Proposition 6.3(2f) as well as the functional schemas (11a and 11b) and Axiom 3d, we obtain
 $\Gamma ^{\ast }\vdash \lnot (\gamma _{ab}@_{i}c_{a}\simeq \delta _{ab}@_{i}c_{a})$
. However, as we shall now show,
$\Gamma ^{\ast }\vdash \lnot (\gamma _{ab}@_{i}c_{a}\simeq \delta _{ab}@_{i}c_{a})$
. However, as we shall now show,
 $\Gamma ^{\ast }\vdash (\gamma _{ab}@_{i}c_{a}\simeq \delta _{ab}@_{i}c_{a})$
, and we have the contradiction. In the first place, since
$\Gamma ^{\ast }\vdash (\gamma _{ab}@_{i}c_{a}\simeq \delta _{ab}@_{i}c_{a})$
, and we have the contradiction. In the first place, since
 $\Phi (\gamma _{ab})=\Phi (\delta _{ab})$
, we have that
$\Phi (\gamma _{ab})=\Phi (\delta _{ab})$
, we have that
 $\Phi (\gamma _{ab})(\Phi (@_{i}c_{a}))=\Phi (\delta _{ab})(\Phi (@_{i}c_{a}))$
and we will prove that
$\Phi (\gamma _{ab})(\Phi (@_{i}c_{a}))=\Phi (\delta _{ab})(\Phi (@_{i}c_{a}))$
and we will prove that
 $\Phi (\gamma _{ab}(@_{i}c_{a}))=\Phi (\delta _{ab}(@_{i}c_{a}))$
. To see this, note that by the definition of
$\Phi (\gamma _{ab}(@_{i}c_{a}))=\Phi (\delta _{ab}(@_{i}c_{a}))$
. To see this, note that by the definition of
 $ \Phi $
, the induction hypothesis for condition (3) of Figure 2, Axiom 3d, then, since either both
$ \Phi $
, the induction hypothesis for condition (3) of Figure 2, Axiom 3d, then, since either both
 $ @_{i_{n}}\gamma _{ab}(@_{i}c_{a})$
and
$ @_{i_{n}}\gamma _{ab}(@_{i}c_{a})$
and
 $\gamma _{ab}(@_{i}c_{a})$
denote or neither of them do, we have that:
$\gamma _{ab}(@_{i}c_{a})$
denote or neither of them do, we have that:-
–
 $\Phi (\gamma _{ab})(\Phi (@_{i}c_{a}))=\Phi (@_{i_{n}}\gamma _{ab}(@_{i}c_{a}))=\Phi (\gamma _{ab}(@_{i}c_{a}))$
, and
$\Phi (\gamma _{ab})(\Phi (@_{i}c_{a}))=\Phi (@_{i_{n}}\gamma _{ab}(@_{i}c_{a}))=\Phi (\gamma _{ab}(@_{i}c_{a}))$
, and -
–
 $\Phi (\delta _{ab})(\Phi (@_{i}c_{a}))=\Phi (@_{i_{n}}\delta _{ab}(@_{i}c_{a}))=\Phi (\delta _{ab}(@_{i}c_{a}))$
.
$\Phi (\delta _{ab})(\Phi (@_{i}c_{a}))=\Phi (@_{i_{n}}\delta _{ab}(@_{i}c_{a}))=\Phi (\delta _{ab}(@_{i}c_{a}))$
.
Therefore,
 $\Phi (\gamma _{ab}(@_{i}c_{a})\kern-0.3pt)\kern1.2pt{=}\kern1.2pt\Phi (\delta _{ab}(@_{i}c_{a}\kern-0.1pt)\kern-0.3pt)$
. Moreover, either
$\Phi (\gamma _{ab}(@_{i}c_{a})\kern-0.3pt)\kern1.2pt{=}\kern1.2pt\Phi (\delta _{ab}(@_{i}c_{a}\kern-0.1pt)\kern-0.3pt)$
. Moreover, either
 $\Gamma ^{\ast }\kern1.2pt{\vdash}\kern1.2pt \mathsf {DEN} (\gamma _{ab}@_{i}c_{a}\kern-0.1pt)$
and
$\Gamma ^{\ast }\kern1.2pt{\vdash}\kern1.2pt \mathsf {DEN} (\gamma _{ab}@_{i}c_{a}\kern-0.1pt)$
and
 $ \Gamma ^{\ast }\vdash \mathsf {DEN}(\delta _{ab}@_{i}c_{a})$
, or
$ \Gamma ^{\ast }\vdash \mathsf {DEN}(\delta _{ab}@_{i}c_{a})$
, or
 $\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(\gamma _{ab}@_{i}c_{a})$
and
$\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(\gamma _{ab}@_{i}c_{a})$
and
 $\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(\delta _{ab}@_{i}c_{a})$
. Hence, by the induction hypothesis and the definition of
$\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(\delta _{ab}@_{i}c_{a})$
. Hence, by the induction hypothesis and the definition of
 $\simeq $
, we have
$\simeq $
, we have
 $\Gamma ^{\ast }\vdash (\gamma _{ab}@_{i}c_{a}\simeq \delta _{ab}@_{i}c_{a})$
. This contradicts our previous statement, which was obtained from the supposition that
$\Gamma ^{\ast }\vdash (\gamma _{ab}@_{i}c_{a}\simeq \delta _{ab}@_{i}c_{a})$
. This contradicts our previous statement, which was obtained from the supposition that
 $\Gamma ^{\ast }\not \vdash \gamma _{ab}\equiv \delta _{ab}$
.
$\Gamma ^{\ast }\not \vdash \gamma _{ab}\equiv \delta _{ab}$
.(
 $\Leftarrow $
) Suppose
$\Leftarrow $
) Suppose
 $\Gamma ^{\ast }\vdash \gamma _{ab}\equiv \delta _{ab}$
. Then,
$\Gamma ^{\ast }\vdash \gamma _{ab}\equiv \delta _{ab}$
. Then,
 $\Gamma ^{\ast }\vdash \gamma _{ab}\simeq \delta _{ab}$
. So by Axiom 11b we have that for any
$\Gamma ^{\ast }\vdash \gamma _{ab}\simeq \delta _{ab}$
. So by Axiom 11b we have that for any
 $\alpha _{a}$
, all the equalities of the form
$\alpha _{a}$
, all the equalities of the form
 $\gamma _{ab}\alpha _{a}\simeq \delta _{ab}\alpha _{a}$
are in
$\gamma _{ab}\alpha _{a}\simeq \delta _{ab}\alpha _{a}$
are in
 $\Gamma ^{\ast }$
. Now, let
$\Gamma ^{\ast }$
. Now, let
 $\Phi (\alpha _{a})$
be some arbitrary element of
$\Phi (\alpha _{a})$
be some arbitrary element of
 $\mathsf {D}_{a}$
. Then we have:
$\mathsf {D}_{a}$
. Then we have:-
–
 $\Phi (\gamma _{ab})(\Phi (\alpha _{a}))=\Phi (@_{i_{n}}\gamma _{ab}(\alpha _{a}))=\Phi (\gamma _{ab}(\alpha _{a}))$
, and
$\Phi (\gamma _{ab})(\Phi (\alpha _{a}))=\Phi (@_{i_{n}}\gamma _{ab}(\alpha _{a}))=\Phi (\gamma _{ab}(\alpha _{a}))$
, and -
–
 $\Phi (\delta _{ab})(\Phi (\alpha _{a}))=\Phi (@_{i_{n}}\delta _{ab}(\alpha _{a}))=\Phi (\delta _{ab}(\alpha _{a}))$
.
$\Phi (\delta _{ab})(\Phi (\alpha _{a}))=\Phi (@_{i_{n}}\delta _{ab}(\alpha _{a}))=\Phi (\delta _{ab}(\alpha _{a}))$
.
So using the equalities
 $\gamma _{ab}\alpha _{a}\simeq \delta _{ab}\alpha _{a}$
that are in
$\gamma _{ab}\alpha _{a}\simeq \delta _{ab}\alpha _{a}$
that are in
 $\Gamma ^{\ast }$
we have that either
$\Gamma ^{\ast }$
we have that either
 $\Gamma ^{\ast }\vdash \mathsf {DEN}(\gamma _{a,b}\alpha _{a})$
and
$\Gamma ^{\ast }\vdash \mathsf {DEN}(\gamma _{a,b}\alpha _{a})$
and
 $\Gamma ^{\ast }\vdash \mathsf {DEN}(\delta _{ab}\alpha _{a})$
and
$\Gamma ^{\ast }\vdash \mathsf {DEN}(\delta _{ab}\alpha _{a})$
and
 $\Gamma ^{\ast }\vdash \gamma _{ab}\alpha _{a}\equiv \delta _{ab}\alpha _{a}$
, or
$\Gamma ^{\ast }\vdash \gamma _{ab}\alpha _{a}\equiv \delta _{ab}\alpha _{a}$
, or
 $\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(\gamma _{ab}\alpha _{a})$
and
$\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(\gamma _{ab}\alpha _{a})$
and
 $\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(\delta _{ab}\alpha _{a})$
. Either way we have that
$\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(\delta _{ab}\alpha _{a})$
. Either way we have that
 $\Phi (\gamma _{ab}\alpha _{a})=\Phi (\delta _{ab}\alpha _{a})$
, as by the induction hypothesis on type b, the first holds by condition (3) from Figure 2, and in the second case both are undefined by condition (2). Therefore,
$\Phi (\gamma _{ab}\alpha _{a})=\Phi (\delta _{ab}\alpha _{a})$
, as by the induction hypothesis on type b, the first holds by condition (3) from Figure 2, and in the second case both are undefined by condition (2). Therefore,
 $\Phi (\gamma _{ab})=\Phi (\delta _{ab})$
.
$\Phi (\gamma _{ab})=\Phi (\delta _{ab})$
. -
This completes our work for kind e, so we turn to kind t. Again we give definitions of
![]() $\Phi $
,
$\Phi $
,
![]() $\mathsf {D}_{ab}$
, and
$\mathsf {D}_{ab}$
, and
![]() $\mathsf {D}_{ab}^{[i]}$
(this time for a function
$\mathsf {D}_{ab}^{[i]}$
(this time for a function
![]() $\left \langle a,b\right \rangle $
of kind t) and then prove two propositions showing that they work as we want.
$\left \langle a,b\right \rangle $
of kind t) and then prove two propositions showing that they work as we want.
Definition 9.11 (
 $\Phi $
,
$\Phi $
,
 $\mathsf {D}_{ab}$
, and
$\mathsf {D}_{ab}$
, and
 $\mathsf {D}_{ab}^{\left [ i\right ] }$
for kind t).
$\mathsf {D}_{ab}^{\left [ i\right ] }$
for kind t).
Let
![]() $\left \langle a,b\right \rangle \in \mathsf {KIND}_{t}$
. Assume that
$\left \langle a,b\right \rangle \in \mathsf {KIND}_{t}$
. Assume that
![]() $\mathsf {D}_{a}$
and
$\mathsf {D}_{a}$
and
![]() $\mathsf {D} _{b}$
have been defined; note that this means that
$\mathsf {D} _{b}$
have been defined; note that this means that
![]() $\Phi (\alpha _{a})$
and
$\Phi (\alpha _{a})$
and
![]() $\Phi (\alpha _{b})$
are defined, for all closed expressions
$\Phi (\alpha _{b})$
are defined, for all closed expressions
![]() $\alpha $
of types a and b respectively. Furthermore, assume that the six conditions in Figure 2 hold for types a and b. Then we define function
$\alpha $
of types a and b respectively. Furthermore, assume that the six conditions in Figure 2 hold for types a and b. Then we define function
![]() $\Gamma $
and global and local domains for this type:
$\Gamma $
and global and local domains for this type:
-
• Let
 $\gamma _{ab}\in \mathsf {CME}_{ab}$
. where
$\gamma _{ab}\in \mathsf {CME}_{ab}$
. where $$ \begin{align*} \begin{array}{llll} \Phi (\gamma _{ab}): & \mathsf{D}_{a} &\rightarrow &\mathsf{D}_{b}\\ &\Phi (\alpha _{a}) & \mapsto & \begin{cases} \begin{array}{ll} \Phi (@_{i_{n}}\gamma _{ab}\alpha _{a}), & \text{ if }\Gamma ^{\ast }\not\vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\equiv \bot _{b}, \\ \Phi (@_{i_{n}}\gamma _{ab}\alpha _{a}) = F_{b}, & \text{ if }\Gamma ^{\ast }\vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\equiv \bot _{b}, \end{array} \end{cases} \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{llll} \Phi (\gamma _{ab}): & \mathsf{D}_{a} &\rightarrow &\mathsf{D}_{b}\\ &\Phi (\alpha _{a}) & \mapsto & \begin{cases} \begin{array}{ll} \Phi (@_{i_{n}}\gamma _{ab}\alpha _{a}), & \text{ if }\Gamma ^{\ast }\not\vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\equiv \bot _{b}, \\ \Phi (@_{i_{n}}\gamma _{ab}\alpha _{a}) = F_{b}, & \text{ if }\Gamma ^{\ast }\vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\equiv \bot _{b}, \end{array} \end{cases} \end{array} \end{align*} $$
 $i_{n}$
is the nominal with least n such that
$i_{n}$
is the nominal with least n such that
 $i_{n}\in \Gamma ^{\ast }$
(since
$i_{n}\in \Gamma ^{\ast }$
(since
 $\Gamma ^{\ast }$
is named, it contains at least one nominal).
$\Gamma ^{\ast }$
is named, it contains at least one nominal).
-
•
 $\mathsf {D}_{ab}=\{ \Phi (\gamma _{ab})\mid \gamma _{ab}\in \mathsf {CME} _{ab}\cap \mathsf {RIGIDS}\} $
.
$\mathsf {D}_{ab}=\{ \Phi (\gamma _{ab})\mid \gamma _{ab}\in \mathsf {CME} _{ab}\cap \mathsf {RIGIDS}\} $
. -
•
 $\mathsf {D}_{ab}^{\left [ i\right ] }=\left \{ \Phi (\gamma _{ab})\mid \gamma _{ab}\in \mathsf {CME}_{ab}\cap \mathsf {RIGIDS}\text { and } \Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\gamma _{ab}))\right \}. $
$\mathsf {D}_{ab}^{\left [ i\right ] }=\left \{ \Phi (\gamma _{ab})\mid \gamma _{ab}\in \mathsf {CME}_{ab}\cap \mathsf {RIGIDS}\text { and } \Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\gamma _{ab}))\right \}. $
Proposition 9.12 (Kind t).
Let
![]() $\Phi $
be as just defined, and let
$\Phi $
be as just defined, and let
![]() $\Phi (\alpha _a),\Phi (\beta _a)\in \mathsf {D}_a$
such that
$\Phi (\alpha _a),\Phi (\beta _a)\in \mathsf {D}_a$
such that
![]() $\Phi (\alpha _a)=\Phi (\beta _a)$
. Then
$\Phi (\alpha _a)=\Phi (\beta _a)$
. Then
![]() $\Phi (@_{i_{n}}\gamma _{ab}\alpha _a)=\Phi (@_{i_{n}}\gamma _{ab}\beta _a)$
.
$\Phi (@_{i_{n}}\gamma _{ab}\alpha _a)=\Phi (@_{i_{n}}\gamma _{ab}\beta _a)$
.
Proof Let
![]() $\Phi (\alpha _{a}),\Phi (\beta _{a})\in \mathsf {D}_{a}$
such that
$\Phi (\alpha _{a}),\Phi (\beta _{a})\in \mathsf {D}_{a}$
such that
![]() $\Phi (\alpha _{a})=\Phi (\beta _{a})$
. By the induction hypothesis on type a, as
$\Phi (\alpha _{a})=\Phi (\beta _{a})$
. By the induction hypothesis on type a, as
![]() $\Gamma ^{\ast }\vdash \mathsf {DEN}(\alpha _{a})$
and
$\Gamma ^{\ast }\vdash \mathsf {DEN}(\alpha _{a})$
and
![]() $\Gamma ^{\ast }\vdash \mathsf {DEN}(\beta _{a})$
we have
$\Gamma ^{\ast }\vdash \mathsf {DEN}(\beta _{a})$
we have
![]() $\Gamma ^{\ast }\vdash \alpha _{a}\equiv \beta _{a}$
. From Proposition 6.3(2c) we get that
$\Gamma ^{\ast }\vdash \alpha _{a}\equiv \beta _{a}$
. From Proposition 6.3(2c) we get that
![]() $\Gamma ^{\ast }\vdash \gamma _{ab}\alpha _{a}\equiv \gamma _{ab}\beta _{a}$
, and so we have
$\Gamma ^{\ast }\vdash \gamma _{ab}\alpha _{a}\equiv \gamma _{ab}\beta _{a}$
, and so we have
![]() $\Gamma ^{\ast }\vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\equiv @_{i_{n}}\gamma _{ab}\beta _{a}$
(using Axioms 3d, 4c, and 8b). Now:
$\Gamma ^{\ast }\vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\equiv @_{i_{n}}\gamma _{ab}\beta _{a}$
(using Axioms 3d, 4c, and 8b). Now:
 $\Phi (\gamma _{ab})(\Phi (\alpha _{a}))= \begin {cases} \begin {array}{ll} \Phi (@_{i_{n}}\gamma _{ab}\alpha _{a}) ,\text { if }\Gamma ^{\ast }\not \vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\equiv \bot _{b}, \\ \Phi (@_{i_{n}}\gamma _{ab}\alpha _{a}) = F_{b} ,\text { if }\Gamma ^{\ast }\vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\equiv \bot _{b}, \end {array} \end {cases}$
$\Phi (\gamma _{ab})(\Phi (\alpha _{a}))= \begin {cases} \begin {array}{ll} \Phi (@_{i_{n}}\gamma _{ab}\alpha _{a}) ,\text { if }\Gamma ^{\ast }\not \vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\equiv \bot _{b}, \\ \Phi (@_{i_{n}}\gamma _{ab}\alpha _{a}) = F_{b} ,\text { if }\Gamma ^{\ast }\vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\equiv \bot _{b}, \end {array} \end {cases}$
 $\Phi (\gamma _{ab})(\Phi (\beta _{a}))= \begin {cases} \begin {array}{ll} \Phi (@_{i_{n}}\gamma _{ab}\beta _{a}) ,\text { if }\Gamma ^{\ast }\not \vdash @_{i_{n}}\gamma _{ab}\beta _{a}\equiv \bot _{b}, \\ \Phi (@_{i_{n}}\gamma _{ab}\beta _{a}) = F_{b} ,\text { if }\Gamma ^{\ast }\vdash @_{i_{n}}\gamma _{ab}\beta _{a}\equiv \bot _{b}. \end {array} \end {cases}$
$\Phi (\gamma _{ab})(\Phi (\beta _{a}))= \begin {cases} \begin {array}{ll} \Phi (@_{i_{n}}\gamma _{ab}\beta _{a}) ,\text { if }\Gamma ^{\ast }\not \vdash @_{i_{n}}\gamma _{ab}\beta _{a}\equiv \bot _{b}, \\ \Phi (@_{i_{n}}\gamma _{ab}\beta _{a}) = F_{b} ,\text { if }\Gamma ^{\ast }\vdash @_{i_{n}}\gamma _{ab}\beta _{a}\equiv \bot _{b}. \end {array} \end {cases}$
From
![]() $\Gamma ^{\ast }\vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\equiv @_{i_{n}}\gamma _{ab}\beta _{a}$
and maximal consistency of
$\Gamma ^{\ast }\vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\equiv @_{i_{n}}\gamma _{ab}\beta _{a}$
and maximal consistency of
![]() $ \Gamma ^{\star }$
it follows that
$ \Gamma ^{\star }$
it follows that
![]() $\Phi (\gamma _{ab})(\Phi (\alpha _{a}))=\Phi (\gamma _{ab})(\Phi (\beta _{a}))$
. The reason is that we have either (1)
$\Phi (\gamma _{ab})(\Phi (\alpha _{a}))=\Phi (\gamma _{ab})(\Phi (\beta _{a}))$
. The reason is that we have either (1)
![]() $\Gamma ^{\ast }\not \vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\equiv \bot _{b}$
and
$\Gamma ^{\ast }\not \vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\equiv \bot _{b}$
and
![]() $\Gamma ^{\ast }\not \vdash @_{i_{n}}\gamma _{ab}\beta _{a}\equiv \bot _{b}$
, or (2)
$\Gamma ^{\ast }\not \vdash @_{i_{n}}\gamma _{ab}\beta _{a}\equiv \bot _{b}$
, or (2)
![]() $\Gamma ^{\ast }\vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\equiv \bot _{b}$
and
$\Gamma ^{\ast }\vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\equiv \bot _{b}$
and
![]() $\Gamma ^{\ast }\vdash @_{i_{n}}\gamma _{ab}\beta _{a}\equiv \bot _{b}$
.
$\Gamma ^{\ast }\vdash @_{i_{n}}\gamma _{ab}\beta _{a}\equiv \bot _{b}$
.
Proposition 9.13 (Kind t).
Let
![]() $\Phi $
,
$\Phi $
,
![]() $\mathsf {D}_{ab}$
, and
$\mathsf {D}_{ab}$
, and
![]() $\mathsf {D} _{ab}^{\left [ i\right ] }$
be as given in Definition 9.11. Then the six conditions in Figure 2 are satisfied.
$\mathsf {D} _{ab}^{\left [ i\right ] }$
be as given in Definition 9.11. Then the six conditions in Figure 2 are satisfied.
Proof We establish these conditions as follows:
-
(1)
 $\mathsf {D}_{ab}=\left \{ \Phi (\gamma _{ab})\mid \gamma _{ab}\in \mathsf {\ CME}_{a}\cap \mathsf {RIGIDS}\text { and }\Gamma ^{\ast }\vdash \mathsf {DEN}(\gamma _{ab})\right \} $
, since by Axiom 8b we have that
$\mathsf {D}_{ab}=\left \{ \Phi (\gamma _{ab})\mid \gamma _{ab}\in \mathsf {\ CME}_{a}\cap \mathsf {RIGIDS}\text { and }\Gamma ^{\ast }\vdash \mathsf {DEN}(\gamma _{ab})\right \} $
, since by Axiom 8b we have that
 $\Gamma ^{\ast }\vdash \mathsf {DEN}(\gamma _{ab})$
.
$\Gamma ^{\ast }\vdash \mathsf {DEN}(\gamma _{ab})$
. -
(2) Since
 $\Gamma ^\ast \vdash \mathsf {DEN}(\gamma _{ab})$
and
$\Gamma ^\ast \vdash \mathsf {DEN}(\gamma _{ab})$
and
 $\Phi (\gamma _{ab})\neq \mathsf {\divideontimes }$
.
$\Phi (\gamma _{ab})\neq \mathsf {\divideontimes }$
. -
(4)
 $\mathsf {D}_{ab}^{\left [ i\right ] }=\left \{ \Phi (\gamma _{ab})\mid \gamma _{ab}\in \mathsf {CME} _{b}\cap \mathsf {RIGIDS}\text { and }\Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\gamma _{ab}))\right \} $
by Definition 9.11. To prove that it is non-empty, we can re-use the argument used in the analogous case in Proposition 9.10 (for
$\mathsf {D}_{ab}^{\left [ i\right ] }=\left \{ \Phi (\gamma _{ab})\mid \gamma _{ab}\in \mathsf {CME} _{b}\cap \mathsf {RIGIDS}\text { and }\Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\gamma _{ab}))\right \} $
by Definition 9.11. To prove that it is non-empty, we can re-use the argument used in the analogous case in Proposition 9.10 (for
 $\mathsf {KIND}_{e}$
functions).
$\mathsf {KIND}_{e}$
functions). -
(5) Since we have
 $\vdash \mathsf {DEN}(\gamma _{ab})$
for
$\vdash \mathsf {DEN}(\gamma _{ab})$
for
 $ \langle a,b\rangle \in \mathsf {KIND}_{t}$
(Axiom 8b), the argument used in Proposition 9.10 (for
$ \langle a,b\rangle \in \mathsf {KIND}_{t}$
(Axiom 8b), the argument used in Proposition 9.10 (for
 $ \mathsf {\ KIND}_{e}$
functions) also works here.
$ \mathsf {\ KIND}_{e}$
functions) also works here. -
(3) Let
 $\gamma _{ab}$
,
$\gamma _{ab}$
,
 $\delta _{ab}\in \mathsf {CME}_{ab}\cap \mathsf {RIGIDS}$
such that
$\delta _{ab}\in \mathsf {CME}_{ab}\cap \mathsf {RIGIDS}$
such that
 $\Gamma ^{\ast }\vdash \mathsf {DEN}(\gamma _{ab})$
and
$\Gamma ^{\ast }\vdash \mathsf {DEN}(\gamma _{ab})$
and
 $\Gamma ^{\ast }\vdash \mathsf {DEN}(\delta _{ab})$
. For the left-to-right implication
$\Gamma ^{\ast }\vdash \mathsf {DEN}(\delta _{ab})$
. For the left-to-right implication
 $\Rightarrow $
, we can use the same argument that we used to prove item (3) in Proposition 9.10 (for
$\Rightarrow $
, we can use the same argument that we used to prove item (3) in Proposition 9.10 (for
 $\mathsf {KIND}_{e}$
functions). For the right-to-left implication
$\mathsf {KIND}_{e}$
functions). For the right-to-left implication
 $\Leftarrow $
we argue as follows. Suppose
$\Leftarrow $
we argue as follows. Suppose
 $\Gamma ^{\ast }\vdash \gamma _{ab}\equiv \delta _{ab}$
. Let
$\Gamma ^{\ast }\vdash \gamma _{ab}\equiv \delta _{ab}$
. Let
 $\Phi (\alpha _{a}) \in \mathsf { \ D}_{a}$
. Then, by Proposition 6.3(2d), we have that
$\Phi (\alpha _{a}) \in \mathsf { \ D}_{a}$
. Then, by Proposition 6.3(2d), we have that
 $\Gamma ^{\ast }\vdash \gamma _{ab}\alpha _{a}\equiv \delta _{ab}\alpha _{a}$
. Since
$\Gamma ^{\ast }\vdash \gamma _{ab}\alpha _{a}\equiv \delta _{ab}\alpha _{a}$
. Since
 $\gamma _{ab} ,\delta _{ab}, \alpha _{a} \in \mathsf {RIGIDS}$
,
$\gamma _{ab} ,\delta _{ab}, \alpha _{a} \in \mathsf {RIGIDS}$
,
 $\Gamma ^{\ast }\vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\equiv @_{i_{n}}\delta _{ab}\alpha _{a}$
. By the induction hypothesis,
$\Gamma ^{\ast }\vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\equiv @_{i_{n}}\delta _{ab}\alpha _{a}$
. By the induction hypothesis,
 $\Phi (@_{i_{n}}\gamma _{ab}\alpha _{a})=\Phi (@_{i_{n}}\delta _{ab}\alpha _{a})$
.
$\Phi (@_{i_{n}}\gamma _{ab}\alpha _{a})=\Phi (@_{i_{n}}\delta _{ab}\alpha _{a})$
.Moreover, by
 $\Gamma ^{\ast }\vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\equiv \bot _{b}$
iff
$\Gamma ^{\ast }\vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\equiv \bot _{b}$
iff
 $\Gamma ^{\ast }\vdash @_{i_{n}}\delta _{ab}\alpha _{a}\equiv \bot _{b}$
. Therefore,
$\Gamma ^{\ast }\vdash @_{i_{n}}\delta _{ab}\alpha _{a}\equiv \bot _{b}$
. Therefore,
 $\Phi (\gamma _{ab})=\Phi (\delta _{ab})$
.
$\Phi (\gamma _{ab})=\Phi (\delta _{ab})$
. -
(6) We want to prove that
 $\Phi (\bot _{ab})=F_{ab}$
. To prove that both functions are the same we have to prove that the value for any argument
$\Phi (\bot _{ab})=F_{ab}$
. To prove that both functions are the same we have to prove that the value for any argument
 $\Phi (\alpha _a)$
is always
$\Phi (\alpha _a)$
is always
 $F_b$
. For any
$F_b$
. For any
 $\alpha _a\in \mathsf {CME}_a\cap \mathsf {RIGIDS}$
and
$\alpha _a\in \mathsf {CME}_a\cap \mathsf {RIGIDS}$
and
 $\Gamma ^\ast \vdash \mathsf {DEN}(\alpha _a)$
we have that two cases:
$\Gamma ^\ast \vdash \mathsf {DEN}(\alpha _a)$
we have that two cases:-
(a)
 $\Gamma ^\ast \vdash \mathsf {EXISTS}(\alpha _a)$
. Then,
$\Gamma ^\ast \vdash \mathsf {EXISTS}(\alpha _a)$
. Then,
 $\vdash \mathsf {EXISTS}(\alpha _{a})\rightarrow \left \langle \lambda x_{a}\bot _{b}\right \rangle (\alpha _{a})\equiv \bot _{b}\frac {\alpha _{a}}{ x_{a}}$
, by Proposition 6.3(2e). As
$\vdash \mathsf {EXISTS}(\alpha _{a})\rightarrow \left \langle \lambda x_{a}\bot _{b}\right \rangle (\alpha _{a})\equiv \bot _{b}\frac {\alpha _{a}}{ x_{a}}$
, by Proposition 6.3(2e). As
 $\bot _{b}$
is a
$\bot _{b}$
is a
 $\mathsf {CME}_{b}$
, we get
$\mathsf {CME}_{b}$
, we get
 $\Gamma ^{\ast }\vdash \left \langle \lambda x_{a}\bot _{b}\right \rangle \left ( \alpha _{a}\right ) \equiv \bot _{b}$
.
$\Gamma ^{\ast }\vdash \left \langle \lambda x_{a}\bot _{b}\right \rangle \left ( \alpha _{a}\right ) \equiv \bot _{b}$
. -
(b)
 $\Gamma ^\ast \vdash \lnot \mathsf {EXISTS}(\alpha _a)$
. By Axiom 11d, we have
$\Gamma ^\ast \vdash \lnot \mathsf {EXISTS}(\alpha _a)$
. By Axiom 11d, we have
 $\vdash (\mathsf {EXISTS}\left \langle \lambda x_{a}\bot _{b}\right \rangle \wedge \lnot (\left \langle \lambda x_{a}\bot _{b}\right \rangle (\alpha _{a})\equiv \bot _{b}))\rightarrow \mathsf {EXISTS}(\alpha _{a})$
. Since,
$\vdash (\mathsf {EXISTS}\left \langle \lambda x_{a}\bot _{b}\right \rangle \wedge \lnot (\left \langle \lambda x_{a}\bot _{b}\right \rangle (\alpha _{a})\equiv \bot _{b}))\rightarrow \mathsf {EXISTS}(\alpha _{a})$
. Since,
 $\vdash \mathsf {EXISTS}\left \langle \lambda x_{a}\bot _{b}\right \rangle $
, by Comprehension Axiom (9a), it follows by propositional logic that
$\vdash \mathsf {EXISTS}\left \langle \lambda x_{a}\bot _{b}\right \rangle $
, by Comprehension Axiom (9a), it follows by propositional logic that
 $\vdash \lnot \mathsf {EXISTS}(\alpha _{a})\rightarrow \left \langle \lambda x_{a}\bot _{b}\right \rangle (\alpha _{a})\equiv \bot _{b}$
. Hence
$\vdash \lnot \mathsf {EXISTS}(\alpha _{a})\rightarrow \left \langle \lambda x_{a}\bot _{b}\right \rangle (\alpha _{a})\equiv \bot _{b}$
. Hence
 $\Gamma ^{\ast }\vdash \left \langle \lambda x_{a}\bot _{b}\right \rangle (\alpha _{a})\equiv \bot _{b}$
. And so, we have
$\Gamma ^{\ast }\vdash \left \langle \lambda x_{a}\bot _{b}\right \rangle (\alpha _{a})\equiv \bot _{b}$
. And so, we have
 $\Gamma ^{\ast }\vdash @_{i_{n}}(\left \langle \lambda x_{a}\bot _{b}\right \rangle (\alpha _{a})\equiv \bot _{b})$
.
$\Gamma ^{\ast }\vdash @_{i_{n}}(\left \langle \lambda x_{a}\bot _{b}\right \rangle (\alpha _{a})\equiv \bot _{b})$
.
Therefore,
 $\Phi (\bot _{ab})=F_{ab}$
.
$\Phi (\bot _{ab})=F_{ab}$
. -
Corollary 9.14. Let
![]() $\alpha _{a}\in \mathsf {CME}_{a}\cap \mathsf {RIGIDS}$
, then
$\alpha _{a}\in \mathsf {CME}_{a}\cap \mathsf {RIGIDS}$
, then
![]() $\Phi (\alpha _{a})= \Phi (@_{j}\alpha _{a})$
for all
$\Phi (\alpha _{a})= \Phi (@_{j}\alpha _{a})$
for all
![]() $j\in \mathsf {NOM}$
.
$j\in \mathsf {NOM}$
.
Proof By Axiom 3d,
![]() $\alpha _{a}\simeq @_{j}\alpha _{a}$
. If
$\alpha _{a}\simeq @_{j}\alpha _{a}$
. If
![]() $\Gamma ^{\ast }\vdash \mathsf {DEN}(\alpha _{a})$
, then
$\Gamma ^{\ast }\vdash \mathsf {DEN}(\alpha _{a})$
, then
![]() $\Phi (\alpha _{a})=$
$\Phi (\alpha _{a})=$
![]() $\Phi (@_{j}\alpha _{a})\not = \divideontimes $
, as
$\Phi (@_{j}\alpha _{a})\not = \divideontimes $
, as
![]() $\Gamma ^{\ast }\vdash \alpha _{a}\equiv @_{j}\alpha _{a}$
(by Proposition 6.3(1b) as well as condition (2) of Figure 2 in
$\Gamma ^{\ast }\vdash \alpha _{a}\equiv @_{j}\alpha _{a}$
(by Proposition 6.3(1b) as well as condition (2) of Figure 2 in
![]() $\Phi $
definition). If
$\Phi $
definition). If
![]() $\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(\alpha _{a})$
then
$\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(\alpha _{a})$
then
![]() $\Phi (\alpha _{a})=\divideontimes = \Phi (@_{j}\alpha _{a})$
(by Proposition 6.3 (1d) and condition (2) of Figure 2).
$\Phi (\alpha _{a})=\divideontimes = \Phi (@_{j}\alpha _{a})$
(by Proposition 6.3 (1d) and condition (2) of Figure 2).
Proposition 9.15. The local partial type hierarchy
![]() $\langle \mathsf {D} _{a}^{[i]}\rangle _{\langle \lbrack i],a\rangle \in W\times \mathsf {TYPES}}$
previously defined has the following properties:
$\langle \mathsf {D} _{a}^{[i]}\rangle _{\langle \lbrack i],a\rangle \in W\times \mathsf {TYPES}}$
previously defined has the following properties:
-
• If
 $\left \langle a,b\right \rangle \in \mathsf {KIND}_{e}$
then
$\left \langle a,b\right \rangle \in \mathsf {KIND}_{e}$
then
 $ \mathsf {D}_{ab}^{[i]}=\left \{ f\in \mathsf {D}_{ab}\mid \mathit {Def} (f)\subseteq \mathsf {D}_{a}^{\left [ i\right ] }\right \}. $
$ \mathsf {D}_{ab}^{[i]}=\left \{ f\in \mathsf {D}_{ab}\mid \mathit {Def} (f)\subseteq \mathsf {D}_{a}^{\left [ i\right ] }\right \}. $
-
• If
 $\left \langle a,b\right \rangle \in \mathsf {KIND}_{t}$
then
$\left \langle a,b\right \rangle \in \mathsf {KIND}_{t}$
then
 $ \mathsf {D}_{ab}^{[i]}=\{f\in \mathsf {D}_{ab}\mid f(\theta )=F_{b}\text { for all }\theta \in \mathsf {D}_{a}-\mathsf {D}_{a}^{\left [ i\right ] }\}$
.
$ \mathsf {D}_{ab}^{[i]}=\{f\in \mathsf {D}_{ab}\mid f(\theta )=F_{b}\text { for all }\theta \in \mathsf {D}_{a}-\mathsf {D}_{a}^{\left [ i\right ] }\}$
.
Proof We first prove the result for
![]() $\left \langle a,b\right \rangle \in \mathsf {KIND}_{e}$
:
$\left \langle a,b\right \rangle \in \mathsf {KIND}_{e}$
:
-
• Let
 $\Phi (\gamma _{ab})\in \mathsf {D}_{ab}^{\left [ i\right ] }$
. So,
$\Phi (\gamma _{ab})\in \mathsf {D}_{ab}^{\left [ i\right ] }$
. So,
 $\gamma _{ab}\in \mathsf {CME}_{ab}\cap \mathsf {RIGIDS}$
and
$\gamma _{ab}\in \mathsf {CME}_{ab}\cap \mathsf {RIGIDS}$
and
 $\Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\gamma _{ab}))$
. We want to prove that
$\Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\gamma _{ab}))$
. We want to prove that
 $\Gamma ^{\ast }\vdash \mathsf {DEN}(\gamma _{ab})$
and also that for any
$\Gamma ^{\ast }\vdash \mathsf {DEN}(\gamma _{ab})$
and also that for any
 $\Phi (\alpha _{a})\in \mathsf {D}_{a}$
such that
$\Phi (\alpha _{a})\in \mathsf {D}_{a}$
such that
 $\Phi (\alpha _{a})\in \mathit {Def}(\Phi \mathsf {(}\gamma _{ab}))$
we get that
$\Phi (\alpha _{a})\in \mathit {Def}(\Phi \mathsf {(}\gamma _{ab}))$
we get that
 $ \Phi (\alpha _{a})\in \mathsf {D}_{a}^{\left [ i\right ] }$
. The first condition follows from the logical theorem
$ \Phi (\alpha _{a})\in \mathsf {D}_{a}^{\left [ i\right ] }$
. The first condition follows from the logical theorem
 $\vdash @_{i}(\mathsf {EXISTS}(\gamma _{ab}))\rightarrow \mathsf {DEN}(\gamma _{ab})$
and the properties of maximal consistent sets.
$\vdash @_{i}(\mathsf {EXISTS}(\gamma _{ab}))\rightarrow \mathsf {DEN}(\gamma _{ab})$
and the properties of maximal consistent sets.For the second condition, take
 $\Phi (\alpha _{a})\in \mathsf {D}_{a}$
such that
$\Phi (\alpha _{a})\in \mathsf {D}_{a}$
such that
 $\Phi (\alpha _{a})\in \mathit {Def}(\Phi \mathsf {(}\gamma _{ab}))$
. Then,
$\Phi (\alpha _{a})\in \mathit {Def}(\Phi \mathsf {(}\gamma _{ab}))$
. Then,
 $\Phi (\gamma _{ab})(\Phi (\alpha _{a}))\not =\divideontimes $
, and by definition,
$\Phi (\gamma _{ab})(\Phi (\alpha _{a}))\not =\divideontimes $
, and by definition,
 $ \Phi (\gamma _{ab})(\Phi (\alpha _{a}))=\Phi (@_{i_{n}}\gamma _{ab}\alpha _{a})$
. Hence, by condition (2) of Figure 2,
$ \Phi (\gamma _{ab})(\Phi (\alpha _{a}))=\Phi (@_{i_{n}}\gamma _{ab}\alpha _{a})$
. Hence, by condition (2) of Figure 2,
 $ \Gamma ^{\ast }\vdash \mathsf {DEN}(@_{i_{n}}\gamma _{ab}\alpha _{a})$
. On the other hand, being
$ \Gamma ^{\ast }\vdash \mathsf {DEN}(@_{i_{n}}\gamma _{ab}\alpha _{a})$
. On the other hand, being
 $\gamma _{ab}$
,
$\gamma _{ab}$
,
 $\alpha _{a}\in \mathsf {RIGIDS}$
, by Axioms 5b, 3d, and 11a we get that
$\alpha _{a}\in \mathsf {RIGIDS}$
, by Axioms 5b, 3d, and 11a we get that
 $\Gamma ^{\ast }\vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\simeq @_{i_{n}}(\gamma _{ab}\alpha _{a})$
and, by Proposition 6.3(1b),
$\Gamma ^{\ast }\vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\simeq @_{i_{n}}(\gamma _{ab}\alpha _{a})$
and, by Proposition 6.3(1b),
 $\Gamma ^{\ast }\vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\equiv @_{i_{n}}(\gamma _{ab}\alpha _{a})$
. We can now use Axiom 8e to get
$\Gamma ^{\ast }\vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\equiv @_{i_{n}}(\gamma _{ab}\alpha _{a})$
. We can now use Axiom 8e to get
 $\Gamma ^{\ast }\vdash \mathsf {DEN}(@_{i_{n}}(\gamma _{ab}\alpha _{a}))$
. And then,
$\Gamma ^{\ast }\vdash \mathsf {DEN}(@_{i_{n}}(\gamma _{ab}\alpha _{a}))$
. And then,
 $\Gamma ^{\ast }\vdash @_{i}\mathsf {DEN}(\gamma _{ab}\alpha _{a})$
(by Proposition 6.3(1e) and Proposition 6.3(1c). Now, using Axiom 11c, Gen
$\Gamma ^{\ast }\vdash @_{i}\mathsf {DEN}(\gamma _{ab}\alpha _{a})$
(by Proposition 6.3(1e) and Proposition 6.3(1c). Now, using Axiom 11c, Gen
 $_{@}$
, and Axiom 1c we have that
$_{@}$
, and Axiom 1c we have that
 $\vdash (@_{i}(\mathsf {EXISTS}(\gamma _{ab}))\wedge @_{i}\mathsf {DEN}(\gamma _{ab}\alpha _{a}))\rightarrow @_{i}(\mathsf {EXISTS}(\alpha _{a}))$
. In consequence,
$\vdash (@_{i}(\mathsf {EXISTS}(\gamma _{ab}))\wedge @_{i}\mathsf {DEN}(\gamma _{ab}\alpha _{a}))\rightarrow @_{i}(\mathsf {EXISTS}(\alpha _{a}))$
. In consequence,
 $\Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\alpha _{a}))$
. Therefore,
$\Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\alpha _{a}))$
. Therefore,
 $\Phi (\alpha _{a})\in \mathsf {D}_{a}^{\left [ i\right ] }$
(as
$\Phi (\alpha _{a})\in \mathsf {D}_{a}^{\left [ i\right ] }$
(as
 $\Phi (\alpha _{a})\in \mathsf {D}_{a}$
).
$\Phi (\alpha _{a})\in \mathsf {D}_{a}$
). -
• Let
 $\Phi (\gamma _{ab})\in \mathsf {D}_{ab}$
,
$\Phi (\gamma _{ab})\in \mathsf {D}_{ab}$
,
 $\gamma _{ab}\in \mathsf {CME}_{ab} \, \cap \, \mathsf {RIGIDS}$
,
$\gamma _{ab}\in \mathsf {CME}_{ab} \, \cap \, \mathsf {RIGIDS}$
,
 $\Gamma ^{\ast }\vdash \mathsf { DEN}(\gamma _{ab})$
and
$\Gamma ^{\ast }\vdash \mathsf { DEN}(\gamma _{ab})$
and
 $\mathit {Def}(\Phi \mathsf {(}\gamma _{ab}))\subseteq \mathsf {D}_{a}^{[i]}$
. Further, suppose that
$\mathit {Def}(\Phi \mathsf {(}\gamma _{ab}))\subseteq \mathsf {D}_{a}^{[i]}$
. Further, suppose that
 $\Gamma ^{\ast }\not \vdash @_{i}(\mathsf {EXISTS}(\gamma _{ab}))$
. By using Axiom 13a, we have that
$\Gamma ^{\ast }\not \vdash @_{i}(\mathsf {EXISTS}(\gamma _{ab}))$
. By using Axiom 13a, we have that
 $\Gamma ^{\ast }\vdash \mathsf {E}(\lnot i\wedge \exists x_{a}(\mathsf {DEN}(\gamma _{ab}x_{a})\wedge @_{i}\lnot (\mathsf {EXISTS} (x_{a}))))$
. Hence, by
$\Gamma ^{\ast }\vdash \mathsf {E}(\lnot i\wedge \exists x_{a}(\mathsf {DEN}(\gamma _{ab}x_{a})\wedge @_{i}\lnot (\mathsf {EXISTS} (x_{a}))))$
. Hence, by
 $\mathsf {E}$
-saturation there is a nominal j such that
$\mathsf {E}$
-saturation there is a nominal j such that
 $\Gamma ^{\ast }\vdash @_{j}(\lnot i\wedge \exists x_{a}(\mathsf {DEN}(\gamma _{ab}x_{a})\wedge @_{i}\lnot (\mathsf {EXISTS}(x_{a}))))$
. That is,
$\Gamma ^{\ast }\vdash @_{j}(\lnot i\wedge \exists x_{a}(\mathsf {DEN}(\gamma _{ab}x_{a})\wedge @_{i}\lnot (\mathsf {EXISTS}(x_{a}))))$
. That is,
 $\Gamma ^{\ast }\vdash @_{j}\lnot i$
and
$\Gamma ^{\ast }\vdash @_{j}\lnot i$
and
 $\Gamma ^{\ast }\vdash @_{j}\exists x_{a}(\mathsf {DEN}(\gamma _{ab}x_{a})\wedge @_{i}\lnot ( \mathsf {EXISTS}(x_{a})))$
. Moreover, by
$\Gamma ^{\ast }\vdash @_{j}\exists x_{a}(\mathsf {DEN}(\gamma _{ab}x_{a})\wedge @_{i}\lnot ( \mathsf {EXISTS}(x_{a})))$
. Moreover, by
 $\exists $
- saturation, there is a constant
$\exists $
- saturation, there is a constant
 $c_{a}$
such that
$c_{a}$
such that
 $\Gamma ^{\ast }\vdash @_{j}(\mathsf {EXISTS}(c_{a}))$
and
$\Gamma ^{\ast }\vdash @_{j}(\mathsf {EXISTS}(c_{a}))$
and
 $\Gamma ^{\ast }\vdash @_{j}(\mathsf {DEN}(\gamma _{ab}@_{j}c_{a})\wedge @_{i}\lnot (\mathsf {EXISTS}(@_{j}c_{a})))$
.
$\Gamma ^{\ast }\vdash @_{j}(\mathsf {DEN}(\gamma _{ab}@_{j}c_{a})\wedge @_{i}\lnot (\mathsf {EXISTS}(@_{j}c_{a})))$
.Putting this all together gives us the contradiction:
-
–
 $\Gamma ^{\ast }\vdash @_{j}(\mathsf {EXISTS}(c_{a}))$
. Thus
$\Gamma ^{\ast }\vdash @_{j}(\mathsf {EXISTS}(c_{a}))$
. Thus
 $ \Gamma ^{\ast }\vdash @_{j}(\mathsf {EXISTS}(@_{j}c_{a}))$
(by Axioms 11a, 3d, and 5b and Proposition 6.3(1b)) and hence
$ \Gamma ^{\ast }\vdash @_{j}(\mathsf {EXISTS}(@_{j}c_{a}))$
(by Axioms 11a, 3d, and 5b and Proposition 6.3(1b)) and hence
 $\Phi (@_{j}c_{a})\in \mathsf {D}_{a}^{[j]}$
.
$\Phi (@_{j}c_{a})\in \mathsf {D}_{a}^{[j]}$
. -
–
 $\Gamma ^{\ast }\vdash @_{j}(\mathsf {DEN}(\gamma _{ab}@_{j}c_{a}))$
. It follows, by Proposition 6.3(1e) that
$\Gamma ^{\ast }\vdash @_{j}(\mathsf {DEN}(\gamma _{ab}@_{j}c_{a}))$
. It follows, by Proposition 6.3(1e) that
 $\Gamma ^{\ast }\vdash \mathsf {DEN}(\gamma _{ab}@_{j}c_{a})$
and thus, by condition (2) in Figure 2, that
$\Gamma ^{\ast }\vdash \mathsf {DEN}(\gamma _{ab}@_{j}c_{a})$
and thus, by condition (2) in Figure 2, that
 $\Phi (\gamma _{ab}@_{j}c_{a})\neq \divideontimes $
. Being rigids and denoting, we easily obtain that
$\Phi (\gamma _{ab}@_{j}c_{a})\neq \divideontimes $
. Being rigids and denoting, we easily obtain that
 $\Gamma ^{\ast }\vdash \gamma _{ab}@_{j}c_{a}\equiv @_{i_{n}}\gamma _{ab}@_{j}c_{a}$
. Now, by condition (3) in Figure 2,
$\Gamma ^{\ast }\vdash \gamma _{ab}@_{j}c_{a}\equiv @_{i_{n}}\gamma _{ab}@_{j}c_{a}$
. Now, by condition (3) in Figure 2,
 $\Phi (\gamma _{ab}@_{j}c_{a})=\Phi (@_{i_{n}}\gamma _{ab}@_{j}c_{a})$
. Hence
$\Phi (\gamma _{ab}@_{j}c_{a})=\Phi (@_{i_{n}}\gamma _{ab}@_{j}c_{a})$
. Hence
 $\Phi (\gamma _{ab})(\Phi (@_{j}c_{a}))=\Phi (@_{i_{n}}\gamma _{ab}@_{j}c_{a})\in \mathsf {D}_{b}$
. Then
$\Phi (\gamma _{ab})(\Phi (@_{j}c_{a}))=\Phi (@_{i_{n}}\gamma _{ab}@_{j}c_{a})\in \mathsf {D}_{b}$
. Then
 $\Phi (@_{j}c_{a})\in \mathit {Def}(\Phi \mathsf {(}\gamma _{ab}))$
$\Phi (@_{j}c_{a})\in \mathit {Def}(\Phi \mathsf {(}\gamma _{ab}))$
-
–
 $\Gamma ^{\ast }\vdash @_{j}@_{i}\lnot (\mathsf {EXISTS}(@_{j}c_{a}))$
. Therefore,
$\Gamma ^{\ast }\vdash @_{j}@_{i}\lnot (\mathsf {EXISTS}(@_{j}c_{a}))$
. Therefore,
 $\Gamma ^{\ast }\vdash \lnot @_{i}(\mathsf {EXISTS}(@_{j}c_{a}))$
by Axioms 3d and 3b. Then
$\Gamma ^{\ast }\vdash \lnot @_{i}(\mathsf {EXISTS}(@_{j}c_{a}))$
by Axioms 3d and 3b. Then
 $\Phi (@_{j}c_{a})\not \in \mathsf {D}_{a}^{[i]}$
.
$\Phi (@_{j}c_{a})\not \in \mathsf {D}_{a}^{[i]}$
.This contradicts the fact that
 $\mathit {Def}(\Phi \mathsf {(}\gamma _{ab}))\subseteq \mathsf {D}_{a}^{[i]}$
. Thus,
$\mathit {Def}(\Phi \mathsf {(}\gamma _{ab}))\subseteq \mathsf {D}_{a}^{[i]}$
. Thus,
 $\Gamma ^{\ast }\vdash @_{i}( \mathsf {EXISTS}(\gamma _{ab}))$
.
$\Gamma ^{\ast }\vdash @_{i}( \mathsf {EXISTS}(\gamma _{ab}))$
.
-
Result for
![]() $\left \langle a,b \right \rangle \in \mathsf {KIND}_{e}$
is proved, so let’s turn to the case for
$\left \langle a,b \right \rangle \in \mathsf {KIND}_{e}$
is proved, so let’s turn to the case for
![]() $\left \langle a,b \right \rangle \in \mathsf {KIND}_{t}$
.
$\left \langle a,b \right \rangle \in \mathsf {KIND}_{t}$
.
-
• Let
 $\Phi (\gamma _{ab})\kern1.2pt{\in}\kern1.2pt \mathsf {D}_{ab}^{\left [ i\right ] }$
. Therefore,
$\Phi (\gamma _{ab})\kern1.2pt{\in}\kern1.2pt \mathsf {D}_{ab}^{\left [ i\right ] }$
. Therefore,
 $\gamma _{ab}\kern1.2pt{\in}\kern1.2pt \mathsf {CME}_{b}\kern1.2pt{\cap}\kern1.2pt \mathsf {RIGIDS}$
and
$\gamma _{ab}\kern1.2pt{\in}\kern1.2pt \mathsf {CME}_{b}\kern1.2pt{\cap}\kern1.2pt \mathsf {RIGIDS}$
and
 $\Gamma ^{\ast }\kern1.2pt{\vdash}\kern1.2pt @_{i}(\mathsf {EXISTS}(\gamma _{ab}))$
. Let
$\Gamma ^{\ast }\kern1.2pt{\vdash}\kern1.2pt @_{i}(\mathsf {EXISTS}(\gamma _{ab}))$
. Let
 $ \Phi (\alpha _{a})\in \mathsf {D}_{a}$
. Suppose that
$ \Phi (\alpha _{a})\in \mathsf {D}_{a}$
. Suppose that
 $\Phi (\gamma _{ab})(\Phi (\alpha _{a}))\neq F_{b}$
. By definition of
$\Phi (\gamma _{ab})(\Phi (\alpha _{a}))\neq F_{b}$
. By definition of
 $\Phi (\gamma _{ab})$
,
$\Phi (\gamma _{ab})$
,
 $\Gamma ^{\ast }\not \vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\equiv \bot _{b} $
. Using Axiom 11d, Gen
$\Gamma ^{\ast }\not \vdash @_{i_{n}}\gamma _{ab}\alpha _{a}\equiv \bot _{b} $
. Using Axiom 11d, Gen
 $_{@}$
, and Axiom 1c and the properties of maximal consistency we have that We also have that
$_{@}$
, and Axiom 1c and the properties of maximal consistency we have that We also have that $$ \begin{align*} \Gamma ^{\ast }\vdash (@_{i}(\mathsf{EXISTS}(\gamma _{ab}))\wedge @_{i}(\lnot (\gamma _{ab}\alpha _{a}\equiv \bot _{b}))\rightarrow @_{i}( \mathsf{\ EXISTS}(\alpha _{a})). \end{align*} $$
$$ \begin{align*} \Gamma ^{\ast }\vdash (@_{i}(\mathsf{EXISTS}(\gamma _{ab}))\wedge @_{i}(\lnot (\gamma _{ab}\alpha _{a}\equiv \bot _{b}))\rightarrow @_{i}( \mathsf{\ EXISTS}(\alpha _{a})). \end{align*} $$
 $\Gamma ^{\ast }\vdash \lnot @_{i}(\gamma _{ab}\alpha _{a}\equiv \bot _{b})$
by using Axiom 3b, the fact that all the expressions involved here are rigid, and Propositions 6.3(2d and 2b). From this we easily obtain that
$\Gamma ^{\ast }\vdash \lnot @_{i}(\gamma _{ab}\alpha _{a}\equiv \bot _{b})$
by using Axiom 3b, the fact that all the expressions involved here are rigid, and Propositions 6.3(2d and 2b). From this we easily obtain that
 $ \Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\alpha _{a}))$
and then
$ \Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\alpha _{a}))$
and then
 $ \Phi (\alpha _{a})\in \mathsf {D}_{a}^{[i]}$
, as required.
$ \Phi (\alpha _{a})\in \mathsf {D}_{a}^{[i]}$
, as required.
-
• Let
 $\Phi (\gamma _{ab})\in \mathsf {D}_{ab}$
such that
$\Phi (\gamma _{ab})\in \mathsf {D}_{ab}$
such that
 $\Phi (\gamma _{ab})(\Phi (\alpha _{a}))=F_{b}\text { for all }\Phi (\alpha _{a})\in \mathsf {D}_{a}-\mathsf {D}_{a}^{[i]}$
, with
$\Phi (\gamma _{ab})(\Phi (\alpha _{a}))=F_{b}\text { for all }\Phi (\alpha _{a})\in \mathsf {D}_{a}-\mathsf {D}_{a}^{[i]}$
, with
 $\gamma _{ab}\in \mathsf {CME} _{b}\cap \mathsf {RIGIDS}$
. Suppose that
$\gamma _{ab}\in \mathsf {CME} _{b}\cap \mathsf {RIGIDS}$
. Suppose that
 $\Gamma ^{\ast }\not \vdash @_{i}(\mathsf {EXISTS}(\gamma _{ab}))$
. Using Axiom 13b, it follows that
$\Gamma ^{\ast }\not \vdash @_{i}(\mathsf {EXISTS}(\gamma _{ab}))$
. Using Axiom 13b, it follows that
 $\Gamma ^{\ast }\vdash \mathsf {E}(\lnot i\wedge \exists x_{a}(\lnot @_{i}( \mathsf {EXISTS}(x_{a}))\wedge \lnot (\gamma _{ab}x_{a}\equiv \bot _{b}))$
. By
$\Gamma ^{\ast }\vdash \mathsf {E}(\lnot i\wedge \exists x_{a}(\lnot @_{i}( \mathsf {EXISTS}(x_{a}))\wedge \lnot (\gamma _{ab}x_{a}\equiv \bot _{b}))$
. By
 $\mathsf {E}$
-saturation there is a nominal j such that
$\mathsf {E}$
-saturation there is a nominal j such that
 $\Gamma ^{\ast }\vdash @_{j}\lnot i$
and
$\Gamma ^{\ast }\vdash @_{j}\lnot i$
and
 $\Gamma ^{\ast }\vdash @_{j}(\exists x_{a}(\lnot @_{i}(\mathsf {EXISTS}(x_{a}))\wedge \lnot (\gamma _{ab}x_{a}\equiv \bot _{b})\,)$
. By
$\Gamma ^{\ast }\vdash @_{j}(\exists x_{a}(\lnot @_{i}(\mathsf {EXISTS}(x_{a}))\wedge \lnot (\gamma _{ab}x_{a}\equiv \bot _{b})\,)$
. By
 $\exists $
-saturation we get that there is a constant
$\exists $
-saturation we get that there is a constant
 $c_{a}$
such that
$c_{a}$
such that
 $\Gamma ^{\ast }\vdash @_{j}(\mathsf {EXISTS}(c_{a}))\ \text {and}\ \Gamma ^{\ast }\vdash @_{j}(\lnot @_{i}(\mathsf {EXISTS}(@_{j}c_{a}))\wedge \lnot (\gamma _{ab}@_{j}c_{a}\equiv \bot _{b}))$
.
$\Gamma ^{\ast }\vdash @_{j}(\mathsf {EXISTS}(c_{a}))\ \text {and}\ \Gamma ^{\ast }\vdash @_{j}(\lnot @_{i}(\mathsf {EXISTS}(@_{j}c_{a}))\wedge \lnot (\gamma _{ab}@_{j}c_{a}\equiv \bot _{b}))$
.Putting this all together yields:
-
–
 $\Gamma ^{\ast }\vdash @_{j}(\mathsf {EXISTS}(c_{a}))$
. Thus
$\Gamma ^{\ast }\vdash @_{j}(\mathsf {EXISTS}(c_{a}))$
. Thus
 $\Gamma ^{\ast }\vdash @_{j}(\mathsf {EXISTS}(@_{j}c_{a}))$
, (by Axiom 5b and Proposition 6.3(1b)), and so
$\Gamma ^{\ast }\vdash @_{j}(\mathsf {EXISTS}(@_{j}c_{a}))$
, (by Axiom 5b and Proposition 6.3(1b)), and so
 $\Phi (@_{j}c_{a})\in \mathsf {D}_{a}^{[j]}$
.
$\Phi (@_{j}c_{a})\in \mathsf {D}_{a}^{[j]}$
. -
–
 $\Gamma ^{\ast }\vdash @_{j}@_{i}\lnot (\mathsf {EXISTS}(@_{j}c_{a}))$
. Thus
$\Gamma ^{\ast }\vdash @_{j}@_{i}\lnot (\mathsf {EXISTS}(@_{j}c_{a}))$
. Thus
 $\Gamma ^{\ast }\vdash \lnot @_{i}(\mathsf {EXISTS}(@_{j}c_{a}))$
and so
$\Gamma ^{\ast }\vdash \lnot @_{i}(\mathsf {EXISTS}(@_{j}c_{a}))$
and so
 $\Phi (@_{j}c_{a})\notin \mathsf {D}_{a}^{[i]}$
.
$\Phi (@_{j}c_{a})\notin \mathsf {D}_{a}^{[i]}$
. -
–
 $\Gamma ^{\ast }\vdash @_{j}\lnot (\gamma _{ab}@_{j}c_{a}\equiv \bot _{b})$
. Thus
$\Gamma ^{\ast }\vdash @_{j}\lnot (\gamma _{ab}@_{j}c_{a}\equiv \bot _{b})$
. Thus
 $\Gamma ^{\ast }\not \vdash @_{i_{n}}\gamma _{ab}@_{j}c_{a}\equiv \bot _{b}$
, by using Axiom 3b, the fact that all the expressions involved here are rigids, and Propositions 6.3(2d and 2b). According to the definition of
$\Gamma ^{\ast }\not \vdash @_{i_{n}}\gamma _{ab}@_{j}c_{a}\equiv \bot _{b}$
, by using Axiom 3b, the fact that all the expressions involved here are rigids, and Propositions 6.3(2d and 2b). According to the definition of
 $\Phi (\gamma _{ab})$
, the value for the argument
$\Phi (\gamma _{ab})$
, the value for the argument
 $\Phi (\gamma _{ab})(\Phi (@_{j}c_{a}))=\Phi (@_{i_{n}}\gamma _{ab}@_{j}c_{a})$
.
$\Phi (\gamma _{ab})(\Phi (@_{j}c_{a}))=\Phi (@_{i_{n}}\gamma _{ab}@_{j}c_{a})$
.
We now consider two possibilities:
-
(1)
 $\Phi (@_{i_{n}}\gamma _{ab}@_{j}c_{a})\neq F_{b}$
. It contradicts the assumption that
$\Phi (@_{i_{n}}\gamma _{ab}@_{j}c_{a})\neq F_{b}$
. It contradicts the assumption that
 $\Phi (\gamma _{ab})(\Phi (\alpha _{a}))=F_{b}$
for all
$\Phi (\gamma _{ab})(\Phi (\alpha _{a}))=F_{b}$
for all
 $\Phi (\alpha _{a})\in \mathsf {D}_{a}-\mathsf {D}_{a}^{[i]}$
, as
$\Phi (\alpha _{a})\in \mathsf {D}_{a}-\mathsf {D}_{a}^{[i]}$
, as
 $\Phi (@_{j}c_{a})\notin \mathsf {D}_{a}^{[i]}$
.
$\Phi (@_{j}c_{a})\notin \mathsf {D}_{a}^{[i]}$
. -
(2)
 $\Phi (@_{i_{n}}\gamma _{ab}@_{j}c_{a})=F_{b}$
. We get
$\Phi (@_{i_{n}}\gamma _{ab}@_{j}c_{a})=F_{b}$
. We get
 $\Phi (@_{i_{n}}\gamma _{ab}@_{j}c_{a})=\Phi (\bot _{b})$
, from condition (6) in Figure 2. By using condition (3) in Figure 2 we get
$\Phi (@_{i_{n}}\gamma _{ab}@_{j}c_{a})=\Phi (\bot _{b})$
, from condition (6) in Figure 2. By using condition (3) in Figure 2 we get
 $\Gamma ^{\ast }\vdash @_{j}\gamma _{ab}@_{i_{n}}c_{a}\equiv \bot _{b}$
, which contradicts the third point above.
$\Gamma ^{\ast }\vdash @_{j}\gamma _{ab}@_{i_{n}}c_{a}\equiv \bot _{b}$
, which contradicts the third point above.
Hence the initial supposition
 $\Gamma ^{\ast }\not \vdash @_{i}(\mathsf {EXISTS}(\gamma _{ab}))$
is false and we have
$\Gamma ^{\ast }\not \vdash @_{i}(\mathsf {EXISTS}(\gamma _{ab}))$
is false and we have
 $\Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\gamma _{ab}))$
. That is,
$\Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\gamma _{ab}))$
. That is,
 $\Phi (\gamma _{ab})\in \mathsf {D}_{ab}^{\left [ i\right ] }$
, as desired.
$\Phi (\gamma _{ab})\in \mathsf {D}_{ab}^{\left [ i\right ] }$
, as desired. -
Lemma 9.16. For any
![]() $d\in \mathsf {D}_{a}$
, there is a nominal i and a constant
$d\in \mathsf {D}_{a}$
, there is a nominal i and a constant
![]() $c_{a}$
such that
$c_{a}$
such that
![]() $d=\Phi (@_{i}c_{a})$
.
$d=\Phi (@_{i}c_{a})$
.
Proof Let
![]() $d\in \mathsf {D}_{a}$
. To prove the lemma we will use the conditions imposed on
$d\in \mathsf {D}_{a}$
. To prove the lemma we will use the conditions imposed on
![]() $\Phi $
and to the partial type hierarchies in Figure 2. By condition (1),
$\Phi $
and to the partial type hierarchies in Figure 2. By condition (1),
![]() $d=\Phi (\alpha _{a})$
for some
$d=\Phi (\alpha _{a})$
for some
![]() $ \alpha _{a}\in \mathsf {CME}_{a}\cap \mathsf {\ RIGIDS}$
such that
$ \alpha _{a}\in \mathsf {CME}_{a}\cap \mathsf {\ RIGIDS}$
such that
![]() $\Gamma ^{\ast }\vdash \mathsf {DEN(}\alpha _{a})$
. By condition (5), there is a nominal i such that
$\Gamma ^{\ast }\vdash \mathsf {DEN(}\alpha _{a})$
. By condition (5), there is a nominal i such that
![]() $d\in \mathsf {D}_{a}^{[i]}$
. By condition (4),
$d\in \mathsf {D}_{a}^{[i]}$
. By condition (4),
![]() $d=\Phi (\alpha _{a})$
is such that
$d=\Phi (\alpha _{a})$
is such that
![]() $\Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\alpha _{a}))$
. By Proposition 6.3(3b),
$\Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\alpha _{a}))$
. By Proposition 6.3(3b),
![]() $ @_{i}\exists x_{a}(x_{a}\equiv \alpha _{a})\in \Gamma ^{\ast }$
, and then, by
$ @_{i}\exists x_{a}(x_{a}\equiv \alpha _{a})\in \Gamma ^{\ast }$
, and then, by
![]() $\exists $
-saturation, there is a constant
$\exists $
-saturation, there is a constant
![]() $c_{a}$
such that
$c_{a}$
such that
![]() $@_{i}( \mathsf {EXISTS}(c_{a}))\in \Gamma ^{\ast }$
and
$@_{i}( \mathsf {EXISTS}(c_{a}))\in \Gamma ^{\ast }$
and
![]() $@_{i}(@_{i}c_{a} \equiv \alpha _{a})\in \Gamma ^{\ast }$
. Hence
$@_{i}(@_{i}c_{a} \equiv \alpha _{a})\in \Gamma ^{\ast }$
. Hence
![]() $\Gamma ^{\ast }\vdash @_{i}c_{a}\equiv \alpha _{a}$
(by Axioms 5a and 3d, as well as Axiom 4 together with Proposition 6.3(1b)). By condition (3), since both
$\Gamma ^{\ast }\vdash @_{i}c_{a}\equiv \alpha _{a}$
(by Axioms 5a and 3d, as well as Axiom 4 together with Proposition 6.3(1b)). By condition (3), since both
![]() $@_{i}c_{a}$
and
$@_{i}c_{a}$
and
![]() $\alpha _{a}$
denote,
$\alpha _{a}$
denote,
![]() $\Gamma ^{\ast }\vdash \mathsf {DEN(}@_{i}c_{a})$
follows easily from the logical theorem
$\Gamma ^{\ast }\vdash \mathsf {DEN(}@_{i}c_{a})$
follows easily from the logical theorem
![]() $\vdash @_{i}(\mathsf {EXISTS}(\alpha _{a}))\rightarrow \mathsf {DEN}(@_{i}\alpha _{a})$
(obtained by Axiom 9b, Gen
$\vdash @_{i}(\mathsf {EXISTS}(\alpha _{a}))\rightarrow \mathsf {DEN}(@_{i}\alpha _{a})$
(obtained by Axiom 9b, Gen
![]() $_{@}$
Rule, Distributivity Axiom 1c, and Proposition 6.3(1c)). Thus, we get
$_{@}$
Rule, Distributivity Axiom 1c, and Proposition 6.3(1c)). Thus, we get
![]() $d=\Phi (@_{i}c_{a})$
, as required.
$d=\Phi (@_{i}c_{a})$
, as required.
Corollary 9.17. For any
![]() $d\in \mathsf {D}_{a}^{[j]}$
, there is a nominal i and a constant
$d\in \mathsf {D}_{a}^{[j]}$
, there is a nominal i and a constant
![]() $c_{a}$
such that
$c_{a}$
such that
![]() $d=\Phi (@_{i}c_{a})$
and
$d=\Phi (@_{i}c_{a})$
and
![]() $ @_{j}(\mathsf {EXISTS}(@_{i}c_{a}))\in \Gamma ^{\ast }$
.
$ @_{j}(\mathsf {EXISTS}(@_{i}c_{a}))\in \Gamma ^{\ast }$
.
Definition 9.18 (Skeleton).
Let
![]() $\mathcal {S}=\langle \langle \mathsf {D}_{a}\rangle _{a\in \mathsf {TYPES}},W,R,\langle \mathsf {D}_{a}^{[i]}\rangle _{\langle \lbrack i],a\rangle \in W\times \mathsf {TYPES}}\rangle $
be defined as:
$\mathcal {S}=\langle \langle \mathsf {D}_{a}\rangle _{a\in \mathsf {TYPES}},W,R,\langle \mathsf {D}_{a}^{[i]}\rangle _{\langle \lbrack i],a\rangle \in W\times \mathsf {TYPES}}\rangle $
be defined as:
-
(1)
 $\langle \mathsf {D}_{a}\rangle _{a\in \mathsf {TYPES}}$
is the partial type hierarchy defined above.
$\langle \mathsf {D}_{a}\rangle _{a\in \mathsf {TYPES}}$
is the partial type hierarchy defined above. -
(2)
 $W=\{[i]\mid i\in \mathsf {NOM}\}$
.
$W=\{[i]\mid i\in \mathsf {NOM}\}$
. -
(3)
 $R=\{\langle \lbrack i],[j]\rangle \mid @_{i}\Diamond j\in \Gamma ^{\ast }\}$
.
$R=\{\langle \lbrack i],[j]\rangle \mid @_{i}\Diamond j\in \Gamma ^{\ast }\}$
. -
(4)
 $\langle \mathsf {D}_{a}^{[i]}\rangle _{\langle \lbrack i],a\rangle \in W\times \mathsf {TYPES}}$
are the local domains defined above.
$\langle \mathsf {D}_{a}^{[i]}\rangle _{\langle \lbrack i],a\rangle \in W\times \mathsf {TYPES}}$
are the local domains defined above.
Proposition 9.19.
![]() $\mathcal {S}=\langle \langle \mathsf {D}_{a}\rangle _{a\in \mathsf {TYPES}},W,R,\langle \mathsf {D}_{a}^{[i]}\rangle _{\langle \lbrack i],a\rangle \in W\times \mathsf {TYPES}}\rangle $
is well defined.
$\mathcal {S}=\langle \langle \mathsf {D}_{a}\rangle _{a\in \mathsf {TYPES}},W,R,\langle \mathsf {D}_{a}^{[i]}\rangle _{\langle \lbrack i],a\rangle \in W\times \mathsf {TYPES}}\rangle $
is well defined.
Proof
![]() $\langle \mathsf {D}_{a}\rangle _{a\in \mathsf {TYPES}}$
is well defined by construction. W and R are also well defined, since
$\langle \mathsf {D}_{a}\rangle _{a\in \mathsf {TYPES}}$
is well defined by construction. W and R are also well defined, since
![]() $ \thickapprox $
is an equivalence relation and R is well defined (see Propositions 9.1 and 9.3). Moreover, using Proposition 9.15 we see that for functional types
$ \thickapprox $
is an equivalence relation and R is well defined (see Propositions 9.1 and 9.3). Moreover, using Proposition 9.15 we see that for functional types
![]() $\left \langle a,b\right \rangle \in \mathsf {KIND}_{e}$
and
$\left \langle a,b\right \rangle \in \mathsf {KIND}_{e}$
and
![]() $ \langle a,b\rangle \in \mathsf {KIND}_{t}$
the local domains
$ \langle a,b\rangle \in \mathsf {KIND}_{t}$
the local domains
![]() $\mathsf {D }_{ab}^{[i]}$
verify the required conditions. Finally,
$\mathsf {D }_{ab}^{[i]}$
verify the required conditions. Finally,
![]() $\langle \mathsf {D} _{a}^{[i]}\rangle _{\langle \lbrack i],a\rangle \in W\times \mathsf {TYPES}}$
is well defined as well. Namely,
$\langle \mathsf {D} _{a}^{[i]}\rangle _{\langle \lbrack i],a\rangle \in W\times \mathsf {TYPES}}$
is well defined as well. Namely,
![]() $i\approx j$
implies
$i\approx j$
implies
![]() $\mathsf {D} _{a}^{[j]}=\mathsf {D}_{a}^{[i]}$
. The reason is the logical theorem
$\mathsf {D} _{a}^{[j]}=\mathsf {D}_{a}^{[i]}$
. The reason is the logical theorem
![]() $\vdash @_{i}j\rightarrow (@_{i}(\mathsf {EXISTS}(\alpha _{a}))\equiv @_{j}(\mathsf {EXISTS}(\alpha _{a})))$
as well as the definitions of the equivalence relation
$\vdash @_{i}j\rightarrow (@_{i}(\mathsf {EXISTS}(\alpha _{a}))\equiv @_{j}(\mathsf {EXISTS}(\alpha _{a})))$
as well as the definitions of the equivalence relation
![]() $\approx $
and of
$\approx $
and of
![]() $ \mathsf {D}_{a}^{[i]}$
over a maximal consistent
$ \mathsf {D}_{a}^{[i]}$
over a maximal consistent
![]() $\Gamma ^{\ast }$
.
$\Gamma ^{\ast }$
.
9.3 Defining the interpretation function
 $\mathsf {I}$
$\mathsf {I}$
Let
![]() $\Gamma ^\ast $
be a named,
$\Gamma ^\ast $
be a named,
![]() $\Diamond $
-saturated,
$\Diamond $
-saturated,
![]() $\exists $
-saturated, and
$\exists $
-saturated, and
![]() $\mathsf {E}$
-saturated and maximal consistent set, and
$\mathsf {E}$
-saturated and maximal consistent set, and
![]() $\mathcal {S}$
the skeleton induced by
$\mathcal {S}$
the skeleton induced by
![]() $\Gamma ^\ast $
. We define
$\Gamma ^\ast $
. We define
![]() $\mathsf {I}$
as the function whose domain is the union of the set of nominals with the set of all non-logical constants of
$\mathsf {I}$
as the function whose domain is the union of the set of nominals with the set of all non-logical constants of
![]() $\mathcal {HPTT}$
.
$\mathcal {HPTT}$
.
![]() $\mathsf {I}$
assigns to each nominal a function from W to the set of truth values. For any constant
$\mathsf {I}$
assigns to each nominal a function from W to the set of truth values. For any constant
![]() $c_a$
we define
$c_a$
we define
![]() $\mathsf {I}(c_a)$
as a function from W to
$\mathsf {I}(c_a)$
as a function from W to
![]() $ \mathsf {D}_a\cup \left \{ \mathsf {\divideontimes }\right \} $
, where
$ \mathsf {D}_a\cup \left \{ \mathsf {\divideontimes }\right \} $
, where
![]() $\mathsf { \ \divideontimes }\not \in \mathsf {D}_a$
for each type
$\mathsf { \ \divideontimes }\not \in \mathsf {D}_a$
for each type
![]() $a\in \mathsf {TYPES}$
. In particular:
$a\in \mathsf {TYPES}$
. In particular:
-
(1)
 $\mathsf {I}(i):W\longrightarrow \left \{ T,F\right \}$
such that
$\mathsf {I}(i):W\longrightarrow \left \{ T,F\right \}$
such that
 $\left [ \mathsf {I}(i)\right ] (\left [ j\right ] )=T$
iff
$\left [ \mathsf {I}(i)\right ] (\left [ j\right ] )=T$
iff
 $i\in \left [ j\right ]$
.
$i\in \left [ j\right ]$
. -
(2) For any constant
 $c_a$
we define
$c_a$
we define
 $\mathsf {I}(c_a):W\longrightarrow \mathsf {D}_a\cup \{\divideontimes \}$
that gives to every
$\mathsf {I}(c_a):W\longrightarrow \mathsf {D}_a\cup \{\divideontimes \}$
that gives to every
 $\left [ i\right ] \in W$
a value in
$\left [ i\right ] \in W$
a value in
 $\mathsf {D}_a$
or is undefined.
$\mathsf {D}_a$
or is undefined. $\left [ \mathsf {I}(c_a)\right ] (\left [ i\right ] )= \begin {cases} \begin {array}{ll} \Phi (@_ic_a) ,\text { if } \Gamma ^{\ast } \vdash \mathsf {DEN}(@_ic_a), \\ \divideontimes ,\text { otherwise.} \end {array} \end {cases}$
$\left [ \mathsf {I}(c_a)\right ] (\left [ i\right ] )= \begin {cases} \begin {array}{ll} \Phi (@_ic_a) ,\text { if } \Gamma ^{\ast } \vdash \mathsf {DEN}(@_ic_a), \\ \divideontimes ,\text { otherwise.} \end {array} \end {cases}$
Proposition 9.20. The pair
![]() $\langle \mathcal {S},\mathsf {I} \rangle $
is a structure (as stipulated in Definition 2.5).
$\langle \mathcal {S},\mathsf {I} \rangle $
is a structure (as stipulated in Definition 2.5).
Proof Clearly,
![]() $i\approx j$
implies
$i\approx j$
implies
![]() $\left [ \mathsf {I}(c_{a})\right ] (\left [ i \right ] )=\left [ \mathsf {I}(c_{a})\right ] (\left [ j\right ] )$
.
$\left [ \mathsf {I}(c_{a})\right ] (\left [ i \right ] )=\left [ \mathsf {I}(c_{a})\right ] (\left [ j\right ] )$
.
The reason is the definition of the equivalence relation
![]() $\approx $
over a maximal consistent
$\approx $
over a maximal consistent
![]() $\Gamma ^{\ast }$
, as well as that
$\Gamma ^{\ast }$
, as well as that
![]() $\vdash @_{i}j\rightarrow \left (@_{i}(c_{a})\simeq @_{j}(c_{a})\right ) $
(consequence of the Gen
$\vdash @_{i}j\rightarrow \left (@_{i}(c_{a})\simeq @_{j}(c_{a})\right ) $
(consequence of the Gen
![]() $_{@}$
Rule and the axioms Intro (3c), @-distributivity (1c), Equality-at-named-worlds (5a), Agree (3d), and transitivity of Equality schema (4c)).
$_{@}$
Rule and the axioms Intro (3c), @-distributivity (1c), Equality-at-named-worlds (5a), Agree (3d), and transitivity of Equality schema (4c)).
Moreover, for any constant
![]() $c_{a}$
with
$c_{a}$
with
![]() $a\in \mathsf {KIND}_{e}$
, by Axiom 8c,
$a\in \mathsf {KIND}_{e}$
, by Axiom 8c,
![]() $\vdash \mathsf {E(DEN}(c_{a}))$
, and then,
$\vdash \mathsf {E(DEN}(c_{a}))$
, and then,
![]() $[\mathsf {I}(c_{a})](\left [ i\right ] )\not =\divideontimes $
for at least one world
$[\mathsf {I}(c_{a})](\left [ i\right ] )\not =\divideontimes $
for at least one world
![]() $\left [ i\right ] \in W$
.
$\left [ i\right ] \in W$
.
Finally, for any constant
![]() $c_{a}$
that denotes at a world
$c_{a}$
that denotes at a world
![]() $\left [ i\right ] \in W$
,
$\left [ i\right ] \in W$
,
![]() $\Gamma ^{\ast }\vdash \mathsf {DEN}(@_{i}c_{a})$
, we have that
$\Gamma ^{\ast }\vdash \mathsf {DEN}(@_{i}c_{a})$
, we have that
![]() $\vdash \mathsf {E}(\mathsf {EXISTS}((@_{i}c_{a})))$
by Proposition 6.3(3a), and thus there exist some world
$\vdash \mathsf {E}(\mathsf {EXISTS}((@_{i}c_{a})))$
by Proposition 6.3(3a), and thus there exist some world
![]() $\left [ j\right ] $
such that
$\left [ j\right ] $
such that
![]() $[\mathsf {I}(c_{a})](\left [ j\right ] )\in \mathsf {D}_{a}^{\left [ j\right ] }$
.
$[\mathsf {I}(c_{a})](\left [ j\right ] )\in \mathsf {D}_{a}^{\left [ j\right ] }$
.
10 Completeness
Suppose we take a named,
![]() $\Diamond $
-saturated,
$\Diamond $
-saturated,
![]() $\exists $
-saturated, and
$\exists $
-saturated, and
![]() $ \mathsf {E}$
-saturated maximal consistent set of sentences
$ \mathsf {E}$
-saturated maximal consistent set of sentences
![]() $\Gamma ^{\ast }$
and induce an
$\Gamma ^{\ast }$
and induce an
![]() $\mathcal {HPTT}$
model
$\mathcal {HPTT}$
model
![]() $\mathcal {M}$
on it (as described in the previous section). Now, suppose we define an arbitrary variable assignment g on
$\mathcal {M}$
on it (as described in the previous section). Now, suppose we define an arbitrary variable assignment g on
![]() $\mathcal {M}$
. This section is devoted to proving that the resulting pair
$\mathcal {M}$
. This section is devoted to proving that the resulting pair
![]() $\left \langle \mathcal {M},g\right \rangle $
will always be a general interpretation (as defined in Definition 2.9). The desired Henkin-style completeness result is an easy corollary.
$\left \langle \mathcal {M},g\right \rangle $
will always be a general interpretation (as defined in Definition 2.9). The desired Henkin-style completeness result is an easy corollary.
One of most useful aspects of the induced structures we defined in the previous section is that the properties of
![]() $\Diamond $
-saturation,
$\Diamond $
-saturation,
![]() $\exists $
-saturation, and
$\exists $
-saturation, and
![]() $\mathsf {E}$
-saturation guarantee us a plentiful supply of rigidified constants and nominals (recall, in particular, Lemma 9.16). In what follows we will use these rigidified expressions to substitute for free variables and free state variables. We start by introducing the notation we will use.
$\mathsf {E}$
-saturation guarantee us a plentiful supply of rigidified constants and nominals (recall, in particular, Lemma 9.16). In what follows we will use these rigidified expressions to substitute for free variables and free state variables. We start by introducing the notation we will use.
Definition 10.1. Let
![]() $\mathcal {M}$
be a
$\mathcal {M}$
be a
![]() $\Gamma ^{\ast }$
induced structure. For each assignment g into
$\Gamma ^{\ast }$
induced structure. For each assignment g into
![]() $\mathcal {M}$
and each expression
$\mathcal {M}$
and each expression
![]() $\beta _{b}$
with
$\beta _{b}$
with
![]() $ \mathsf {FREE}(\beta _{b})=\{x_{a_{1}},\dots ,x_{a_{m}}\}$
and
$ \mathsf {FREE}(\beta _{b})=\{x_{a_{1}},\dots ,x_{a_{m}}\}$
and
![]() $\mathsf {SFREE} (\beta _{b})=\{s_{1},\dots ,s_{p}\}$
, we define
$\mathsf {SFREE} (\beta _{b})=\{s_{1},\dots ,s_{p}\}$
, we define
 $$ \begin{align*} (\beta _{b})^{\widehat{g}}:=\beta _{b}\frac{@_{i_{n_{1}}}c_{a_{1}}\ldots @_{i_{n_{m}}}c_{a_{m}}}{{x_{a_{1}}\ldots x_{a_{m}}}}\frac{j_{1}\ldots j_{p}}{ s_{1}\ldots s_{p}}, \end{align*} $$
$$ \begin{align*} (\beta _{b})^{\widehat{g}}:=\beta _{b}\frac{@_{i_{n_{1}}}c_{a_{1}}\ldots @_{i_{n_{m}}}c_{a_{m}}}{{x_{a_{1}}\ldots x_{a_{m}}}}\frac{j_{1}\ldots j_{p}}{ s_{1}\ldots s_{p}}, \end{align*} $$
where
![]() $c_{a_{1}}$
,…,
$c_{a_{1}}$
,…,
![]() $c_{a_{m}}$
are the first constants of appropriate types that are in
$c_{a_{m}}$
are the first constants of appropriate types that are in
![]() $\Gamma ^{\ast }$
and
$\Gamma ^{\ast }$
and
![]() $i_{n_{1}},\ldots ,i_{n_{m}}$
are the nominals with lowest
$i_{n_{1}},\ldots ,i_{n_{m}}$
are the nominals with lowest
![]() $n_{k}$
such that
$n_{k}$
such that
![]() $g(x_{a_{k}})=\Phi (@_{i_{n_{k}}}c_{ak})$
and
$g(x_{a_{k}})=\Phi (@_{i_{n_{k}}}c_{ak})$
and
![]() $j_{1},\ldots ,j_{p}$
are the nominals with lowest index such that
$j_{1},\ldots ,j_{p}$
are the nominals with lowest index such that
![]() $g(s_{r})=[j_{r}]$
. This “official” notation is a little cumbersome, so we sometimes simplify it to
$g(s_{r})=[j_{r}]$
. This “official” notation is a little cumbersome, so we sometimes simplify it to
Remark 10.2. When we write
![]() $(\xi _{b})^{\widehat {g}}$
the substitution
$(\xi _{b})^{\widehat {g}}$
the substitution
![]() $\widehat {g}$
is linked to expression
$\widehat {g}$
is linked to expression
![]() $\xi _{b}$
and only free variables and state variables are affected. The substitution order is irrelevant as variables are replaced by closed expressions. When
$\xi _{b}$
and only free variables and state variables are affected. The substitution order is irrelevant as variables are replaced by closed expressions. When
![]() $\xi _{b}$
is a complex expression like
$\xi _{b}$
is a complex expression like
![]() $\alpha _{a}\equiv \delta _{a}$
or
$\alpha _{a}\equiv \delta _{a}$
or
![]() $\gamma _{ab}\alpha _{a}$
one can rewrite
$\gamma _{ab}\alpha _{a}$
one can rewrite
![]() $(\alpha _{a}\equiv \delta _{a})^{\widehat { g}}$
as
$(\alpha _{a}\equiv \delta _{a})^{\widehat { g}}$
as
![]() $(\alpha _{a})^{\widehat {g}}\equiv (\delta _{a})^{\widehat {g}}$
and
$(\alpha _{a})^{\widehat {g}}\equiv (\delta _{a})^{\widehat {g}}$
and
![]() $ (\gamma _{ab}\alpha _{a})^{\widehat {g}}$
as
$ (\gamma _{ab}\alpha _{a})^{\widehat {g}}$
as
![]() $(\gamma _{ab})^{\widehat {g} }(\alpha _{a})^{\widehat {g}}$
because variables not appearing free in
$(\gamma _{ab})^{\widehat {g} }(\alpha _{a})^{\widehat {g}}$
because variables not appearing free in
![]() $ \alpha _{a}$
,
$ \alpha _{a}$
,
![]() $\delta _{a}$
, or
$\delta _{a}$
, or
![]() $\gamma _{ab}$
remain unaltered. Moreover, if
$\gamma _{ab}$
remain unaltered. Moreover, if
![]() $\ \widehat {g}$
is linked to expression
$\ \widehat {g}$
is linked to expression
![]() $\exists x_{a}\varphi $
or
$\exists x_{a}\varphi $
or
![]() $ \left \langle \lambda x_{a}\varphi \right \rangle $
, substitution
$ \left \langle \lambda x_{a}\varphi \right \rangle $
, substitution
![]() $(\exists x_{a}\varphi )^{\widehat {g}}$
or
$(\exists x_{a}\varphi )^{\widehat {g}}$
or
![]() $\left \langle \lambda x_{a}\varphi \right \rangle ^{\widehat {g}}$
does not change variable
$\left \langle \lambda x_{a}\varphi \right \rangle ^{\widehat {g}}$
does not change variable
![]() $x_{a}$
and when we write
$x_{a}$
and when we write
![]() $(\varphi )^{\widehat {g}}$
in the same proof, variable
$(\varphi )^{\widehat {g}}$
in the same proof, variable
![]() $ x_{a}$
is not replaced. In case we wanted to replace
$ x_{a}$
is not replaced. In case we wanted to replace
![]() $x_{a} $
, we need to introduce another
$x_{a} $
, we need to introduce another
![]() $\widehat {g^{\prime }}$
linked to
$\widehat {g^{\prime }}$
linked to
![]() $\varphi $
.
$\varphi $
.
Theorem 10.3. Let
![]() $\mathcal {M}$
be the structure induced by a
$\mathcal {M}$
be the structure induced by a
![]() $\Diamond $
-saturated,
$\Diamond $
-saturated,
![]() $ \exists $
-saturated, and
$ \exists $
-saturated, and
![]() $\mathsf {E}$
-saturated maximal consistent set of sentences
$\mathsf {E}$
-saturated maximal consistent set of sentences
![]() $\Gamma ^{\ast }$
, and let g be an assignment function on
$\Gamma ^{\ast }$
, and let g be an assignment function on
![]() $ \mathcal {M}$
. Then for each expression
$ \mathcal {M}$
. Then for each expression
![]() $\beta _{b}\in \mathsf {ME}_{b}$
and any
$\beta _{b}\in \mathsf {ME}_{b}$
and any
![]() $i\in \mathsf {NOM}$
:
$i\in \mathsf {NOM}$
:
(i.e., both are defined and equal or both are undefined).
Proof The proof is by induction on the complexity of the expressions. For existential formulas as well as lambda and function application expressions the proof follows. The remaining cases are in Appendix 12.4.
-
(1) Existential formulas: We want to prove that
 $[[\exists x_{a}\varphi ]]^{ \mathcal {M} ,[i],g}=\Phi (@_{i}(\exists x_{a}\varphi )^{\widehat {g}})$
.
$[[\exists x_{a}\varphi ]]^{ \mathcal {M} ,[i],g}=\Phi (@_{i}(\exists x_{a}\varphi )^{\widehat {g}})$
.For left-to-right direction, let
 $[[\exists x_{a}\varphi ]]^{\mathcal {M },[i],g}=T$
, then there is a
$[[\exists x_{a}\varphi ]]^{\mathcal {M },[i],g}=T$
, then there is a
 $\theta \in \mathsf {D}_{a}^{[i]}$
such that
$\theta \in \mathsf {D}_{a}^{[i]}$
such that
 $ [[\varphi ]]^{\mathcal {M},[i],g_{x_{a}}^{\theta }}=T$
. By Corollary 9.17, there exist a nominal j and a constant
$ [[\varphi ]]^{\mathcal {M},[i],g_{x_{a}}^{\theta }}=T$
. By Corollary 9.17, there exist a nominal j and a constant
 $c_{a}$
such that
$c_{a}$
such that
 $\theta =\Phi (@_{j}c_{a})$
and
$\theta =\Phi (@_{j}c_{a})$
and
 $\Gamma ^{\ast }\vdash @_{i}( \mathsf {EXISTS(}@_{j}c_{a}))$
. Assume that j and
$\Gamma ^{\ast }\vdash @_{i}( \mathsf {EXISTS(}@_{j}c_{a}))$
. Assume that j and
 $c_{a}$
are the first nominal and constant with this property. Thus,
$c_{a}$
are the first nominal and constant with this property. Thus,
 $@_{i}(\varphi )^{\widehat {g_{x_{a}}^{\Phi (@_{j}c_{a})}}}\in \Gamma ^{\ast }$
, and
$@_{i}(\varphi )^{\widehat {g_{x_{a}}^{\Phi (@_{j}c_{a})}}}\in \Gamma ^{\ast }$
, and
 $\Phi (@_{i}(\varphi )^{\widehat {g_{x_{a}}^{\Phi (@_{j}c_{a})}}})=T$
by induction hypothesis.
$\Phi (@_{i}(\varphi )^{\widehat {g_{x_{a}}^{\Phi (@_{j}c_{a})}}})=T$
by induction hypothesis.Due to the value of variable
 $x_{a}$
in the assignment
$x_{a}$
in the assignment
 $g_{x_{a}}^{\Phi (@_{j}c_{a})}$
,
$g_{x_{a}}^{\Phi (@_{j}c_{a})}$
,
 $@_{i}(\varphi )^{\widehat {g_{x_{a}}^{\Phi (@_{j}c_{a})}}} :=@_{i} (\varphi )\widehat {{}^{g}}\frac {@_{j}c_{a}}{x_{a}}$
(as
$@_{i}(\varphi )^{\widehat {g_{x_{a}}^{\Phi (@_{j}c_{a})}}} :=@_{i} (\varphi )\widehat {{}^{g}}\frac {@_{j}c_{a}}{x_{a}}$
(as
 $\widehat {g}$
only substitutes free variables in
$\widehat {g}$
only substitutes free variables in
 $\exists x_{a}\varphi $
) and so
$\exists x_{a}\varphi $
) and so
 $\Gamma ^{\ast }\vdash @_{i}(\varphi )\widehat {{}^{g}}\frac {@_{j}c_{a}}{x_{a}}$
. By Quantifier schema 2b, Gen
$\Gamma ^{\ast }\vdash @_{i}(\varphi )\widehat {{}^{g}}\frac {@_{j}c_{a}}{x_{a}}$
. By Quantifier schema 2b, Gen
 $_{@}$
, and @-distributivity Axiom 1c, we get
$_{@}$
, and @-distributivity Axiom 1c, we get
 $\vdash @_{i}(\mathsf {EXISTS}(@_{j}c_{a}))\wedge @_{i}((\varphi )^{ \widehat {g}}\frac {@_{j}c_{a}}{x_{a}})\rightarrow @_{i}(\exists x_{a}\varphi )^{\widehat {g}}$
. Therefore,
$\vdash @_{i}(\mathsf {EXISTS}(@_{j}c_{a}))\wedge @_{i}((\varphi )^{ \widehat {g}}\frac {@_{j}c_{a}}{x_{a}})\rightarrow @_{i}(\exists x_{a}\varphi )^{\widehat {g}}$
. Therefore,
 $\Gamma ^{\ast }\vdash @_{i}(\exists x_{a}\varphi )^{\widehat {g}}$
and so
$\Gamma ^{\ast }\vdash @_{i}(\exists x_{a}\varphi )^{\widehat {g}}$
and so
 $\Phi (@_{i}(\exists x_{a}\varphi )^{\widehat {g}})=T$
.
$\Phi (@_{i}(\exists x_{a}\varphi )^{\widehat {g}})=T$
.Now, for the right-to-left direction, suppose that
 $\Phi (@_{i}(\exists x_{a}\varphi )^{\widehat {g}})=T$
, then
$\Phi (@_{i}(\exists x_{a}\varphi )^{\widehat {g}})=T$
, then
 $\Gamma ^{\ast }\vdash @_{i}(\exists x_{a}\varphi )^{\widehat {g}}$
. As
$\Gamma ^{\ast }\vdash @_{i}(\exists x_{a}\varphi )^{\widehat {g}}$
. As
 $\Gamma ^{\ast }$
is
$\Gamma ^{\ast }$
is
 $\exists $
-saturated, there is a constant
$\exists $
-saturated, there is a constant
 $c_{a}$
such that
$c_{a}$
such that
 $@_{i}(\mathsf {EXISTS}(@_{i}c_{a}))\in \Gamma ^{\ast }\text { and } @_{i}(\varphi )^{\widehat {g}}\frac {@_{i}c_{a}}{x_{a}}\in \Gamma ^{\ast }$
(the substitutions in
$@_{i}(\mathsf {EXISTS}(@_{i}c_{a}))\in \Gamma ^{\ast }\text { and } @_{i}(\varphi )^{\widehat {g}}\frac {@_{i}c_{a}}{x_{a}}\in \Gamma ^{\ast }$
(the substitutions in
 $\widehat {g}$
only changes free variables at
$\widehat {g}$
only changes free variables at
 $\exists x_{a}\varphi $
and so variable
$\exists x_{a}\varphi $
and so variable
 $x_{a}$
is not replaced). Then
$x_{a}$
is not replaced). Then
 $\Phi (@_{i}c_{a})\ \in \mathsf {D}_{a}^{[i]}$
. Let
$\Phi (@_{i}c_{a})\ \in \mathsf {D}_{a}^{[i]}$
. Let
 $\theta =\Phi (@_{i}c_{a})$
, then
$\theta =\Phi (@_{i}c_{a})$
, then
 $\Gamma ^{\ast }\vdash @_{i}(\varphi )^{\widehat {g_{x_{a}}^{\theta }}} $
and so
$\Gamma ^{\ast }\vdash @_{i}(\varphi )^{\widehat {g_{x_{a}}^{\theta }}} $
and so
 $\Phi (@_{i}(\varphi )^{\widehat {g_{x_{a}}^{\theta }}})=T$
. Thus
$\Phi (@_{i}(\varphi )^{\widehat {g_{x_{a}}^{\theta }}})=T$
. Thus
 $[[\varphi ]]^{ \mathcal {M},[i],g_{x_{a}}^{\theta }}=T$
. Therefore,
$[[\varphi ]]^{ \mathcal {M},[i],g_{x_{a}}^{\theta }}=T$
. Therefore,
 $[[\exists x_{a}\varphi ]]^{\mathcal {M},[i],g}=T$
, as desired.
$[[\exists x_{a}\varphi ]]^{\mathcal {M},[i],g}=T$
, as desired. -
(2) Function applications: We treat
 $\left \langle a,b\right \rangle \in \mathsf {KIND}_{e}$
and
$\left \langle a,b\right \rangle \in \mathsf {KIND}_{e}$
and
 $\left \langle a,b\right \rangle \in \mathsf {KIND}_{t}$
separately.
$\left \langle a,b\right \rangle \in \mathsf {KIND}_{t}$
separately.Let
 $\left \langle a,b\right \rangle \in \mathsf {KIND}_{e}$
. We need to show that
$\left \langle a,b\right \rangle \in \mathsf {KIND}_{e}$
. We need to show that
 $[[\gamma _{ab}\alpha _{a}]]^{\mathcal {M},[i],g}=\Phi (@_{i}(\gamma _{ab}\alpha _{a})^{\widehat {g}})$
. By definition,
$[[\gamma _{ab}\alpha _{a}]]^{\mathcal {M},[i],g}=\Phi (@_{i}(\gamma _{ab}\alpha _{a})^{\widehat {g}})$
. By definition,
 $\lbrack \lbrack \gamma _{ab}\alpha _{a}]]^{\mathcal {M},[i],g}=[[\gamma _{ab}]]^{\mathcal {M},[i],g}\left ( [[\alpha _{a}]]^{\mathcal {M},[i],g}\right )$
if
$\lbrack \lbrack \gamma _{ab}\alpha _{a}]]^{\mathcal {M},[i],g}=[[\gamma _{ab}]]^{\mathcal {M},[i],g}\left ( [[\alpha _{a}]]^{\mathcal {M},[i],g}\right )$
if
 $[[\gamma _{ab}]]^{\mathcal {M},[i],g}\not =\divideontimes $
and
$[[\gamma _{ab}]]^{\mathcal {M},[i],g}\not =\divideontimes $
and
 $[[\alpha _{a}]]^{\mathcal {M},[i],g}\not =\divideontimes $
; and it is undefined otherwise. In the first case the result could be undefined as
$[[\alpha _{a}]]^{\mathcal {M},[i],g}\not =\divideontimes $
; and it is undefined otherwise. In the first case the result could be undefined as
 $[[\gamma _{ab}]]^{\mathcal {M },[i],g}$
is a partial function. By the induction hypothesis we have that
$[[\gamma _{ab}]]^{\mathcal {M },[i],g}$
is a partial function. By the induction hypothesis we have that
 $ [[\gamma _{ab}]]^{\mathcal {M},[i],g}=\Phi (@_{i}(\gamma _{ab})^{\widehat {g}}) $
and
$ [[\gamma _{ab}]]^{\mathcal {M},[i],g}=\Phi (@_{i}(\gamma _{ab})^{\widehat {g}}) $
and
 $[[\alpha _{a}]]^{\mathcal {M},[i],g}=\Phi (@_{i}(\alpha _{a})^{ \widehat {g}})$
.
$[[\alpha _{a}]]^{\mathcal {M},[i],g}=\Phi (@_{i}(\alpha _{a})^{ \widehat {g}})$
.-
• We first treat the case when function and argument are both defined,
 $[[\gamma _{ab}]]^{\mathcal {M},[i],g}\neq \divideontimes $
and
$[[\gamma _{ab}]]^{\mathcal {M},[i],g}\neq \divideontimes $
and
 $[[\alpha _{a}]]^{\mathcal {M},[i],g}\neq \divideontimes $
. By definition of
$[[\alpha _{a}]]^{\mathcal {M},[i],g}\neq \divideontimes $
. By definition of
 $\Phi $
, we have that
$\Phi $
, we have that
 $\lbrack \lbrack \gamma _{ab}]]^{\mathcal {M},[i],g}\left ( [[\alpha _{a}]]^{ \mathcal {M},[i],g}\right ) = \Phi (@_{i}(\gamma _{ab})^{\widehat {g}})(\Phi (@_{i}(\alpha _{a})^{\widehat {g}}))=\Phi (@_{i_{n}}(@_{i}(\gamma _{ab})^{\widehat {g}})(@_{i}(\alpha _{a})^{\widehat {g}}))$
. As already mentioned, the final result could be defined (
$\lbrack \lbrack \gamma _{ab}]]^{\mathcal {M},[i],g}\left ( [[\alpha _{a}]]^{ \mathcal {M},[i],g}\right ) = \Phi (@_{i}(\gamma _{ab})^{\widehat {g}})(\Phi (@_{i}(\alpha _{a})^{\widehat {g}}))=\Phi (@_{i_{n}}(@_{i}(\gamma _{ab})^{\widehat {g}})(@_{i}(\alpha _{a})^{\widehat {g}}))$
. As already mentioned, the final result could be defined (
 $[[\gamma _{ab}\alpha _{a}]]^{\mathcal {M},[i],g}\not =\divideontimes $
) or undefined ((
$[[\gamma _{ab}\alpha _{a}]]^{\mathcal {M},[i],g}\not =\divideontimes $
) or undefined ((
 $ [[\gamma _{ab}\alpha _{a}]]^{\mathcal {M},[i],g}=\divideontimes $
). In the first case, by condition (2) in Figure 2, we have that
$ [[\gamma _{ab}\alpha _{a}]]^{\mathcal {M},[i],g}=\divideontimes $
). In the first case, by condition (2) in Figure 2, we have that
 $\Gamma ^{\ast }\vdash \mathsf {DEN}(@_{i_{n}}(@_{i}(\gamma _{ab})^{\widehat {g}})(@_{i}(\alpha _{a})^{\widehat {g}}))$
. Then,
$\Gamma ^{\ast }\vdash \mathsf {DEN}(@_{i_{n}}(@_{i}(\gamma _{ab})^{\widehat {g}})(@_{i}(\alpha _{a})^{\widehat {g}}))$
. Then,
 $\Phi (@_{i_{n}}(@_{i}(\gamma _{ab})^{\widehat {g}})(@_{i}(\alpha _{a})^{ \widehat {g}}))=\Phi (@_{i}(\gamma _{ab}\alpha _{a})^{\widehat {g}})$
, as
$\Phi (@_{i_{n}}(@_{i}(\gamma _{ab})^{\widehat {g}})(@_{i}(\alpha _{a})^{ \widehat {g}}))=\Phi (@_{i}(\gamma _{ab}\alpha _{a})^{\widehat {g}})$
, as
 $\Gamma ^{\ast }\vdash @_{i_{n}}(@_{i}(\gamma _{ab})^{\widehat {g} })(@_{i}(\alpha _{a})^{\widehat {g}}))\equiv @_{i}(\gamma _{ab}\alpha _{a})^{ \widehat {g}}$
. To prove the later result we use Axioms 3d, 11b, and 5b, Proposition 6.3(1b), and condition (3) in Figure 2. Therefore,
$\Gamma ^{\ast }\vdash @_{i_{n}}(@_{i}(\gamma _{ab})^{\widehat {g} })(@_{i}(\alpha _{a})^{\widehat {g}}))\equiv @_{i}(\gamma _{ab}\alpha _{a})^{ \widehat {g}}$
. To prove the later result we use Axioms 3d, 11b, and 5b, Proposition 6.3(1b), and condition (3) in Figure 2. Therefore,
 $[[\gamma _{ab}\alpha _{a}]]^{\mathcal {M},[i],g}=\Phi (@_{i}(\gamma _{ab}\alpha _{a})^{\widehat {g}})$
as required.
$[[\gamma _{ab}\alpha _{a}]]^{\mathcal {M},[i],g}=\Phi (@_{i}(\gamma _{ab}\alpha _{a})^{\widehat {g}})$
as required.When the function application is undefined, by the definition of
 $\Phi $
:
$\Phi $
: $\divideontimes = \Phi (@_{i}(\gamma _{ab})^{\widehat {g} })(\Phi (@_{i}(\alpha _{a})^{\widehat {g}})) = \Phi (@_{i_{n}}(@_{i}(\gamma _{ab})^{\widehat {g}})(@_{i}(\alpha _{a})^{ \widehat {g}}))$
. Thus, by condition (2) in Figure 2,
$\divideontimes = \Phi (@_{i}(\gamma _{ab})^{\widehat {g} })(\Phi (@_{i}(\alpha _{a})^{\widehat {g}})) = \Phi (@_{i_{n}}(@_{i}(\gamma _{ab})^{\widehat {g}})(@_{i}(\alpha _{a})^{ \widehat {g}}))$
. Thus, by condition (2) in Figure 2,
 $\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(@_{i_{n}}(@_{i}(\gamma _{ab})^{\widehat {g}})(@_{i}(\alpha _{a})^{\widehat {g}}))$
. To arrive to the conclusion that
$\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(@_{i_{n}}(@_{i}(\gamma _{ab})^{\widehat {g}})(@_{i}(\alpha _{a})^{\widehat {g}}))$
. To arrive to the conclusion that
 $\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(@_{i}(\gamma _{ab}(\alpha _{a}))^{\widehat {g}})$
one can apply the same axioms and proposition used above.
$\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(@_{i}(\gamma _{ab}(\alpha _{a}))^{\widehat {g}})$
one can apply the same axioms and proposition used above. -
• Let us consider the case when either the function or the argument are undefined. When the function is undefined, by the induction hypothesis we have
 $\lbrack \lbrack \gamma _{ab}]]^{\mathcal {M},[i],g}=\divideontimes =\Phi (@_{i}(\gamma _{ab})^{\widehat {g}})$
. This implies
$\lbrack \lbrack \gamma _{ab}]]^{\mathcal {M},[i],g}=\divideontimes =\Phi (@_{i}(\gamma _{ab})^{\widehat {g}})$
. This implies
 $\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(@_{i}(\gamma _{ab})^{\widehat {g}})$
, according to condition (2) in Figure 2. Therefore,
$\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(@_{i}(\gamma _{ab})^{\widehat {g}})$
, according to condition (2) in Figure 2. Therefore,
 $\Gamma ^{\ast }\vdash \lnot \mathsf {DEN }(@_{i}(\gamma _{ab}(\alpha _{a}))^{\widehat {g}})$
(by Axioms 8d and 5b and Proposition 6.3(1d)). Thus,
$\Gamma ^{\ast }\vdash \lnot \mathsf {DEN }(@_{i}(\gamma _{ab}(\alpha _{a}))^{\widehat {g}})$
(by Axioms 8d and 5b and Proposition 6.3(1d)). Thus,
 $\Phi (@_{i}(\gamma _{ab}\alpha _{a})^{ \widehat {g}})=\divideontimes $
, as we wanted to prove.
$\Phi (@_{i}(\gamma _{ab}\alpha _{a})^{ \widehat {g}})=\divideontimes $
, as we wanted to prove.When the argument is undefined, the proof is similar.
Let
 $\left \langle a,b\right \rangle \in \mathsf {KIND}_{t}$
. We need to show that
$\left \langle a,b\right \rangle \in \mathsf {KIND}_{t}$
. We need to show that
 $[[\gamma _{ab}\alpha _{a}]]^{\mathcal {M},[i],g}=\Phi (@_{i}(\gamma _{ab}\alpha _{a})^{\widehat {g}})$
. By definition,
$[[\gamma _{ab}\alpha _{a}]]^{\mathcal {M},[i],g}=\Phi (@_{i}(\gamma _{ab}\alpha _{a})^{\widehat {g}})$
. By definition,
 $\lbrack \lbrack \gamma _{ab}\alpha _{a}]]^{\mathcal {M},[i],g}=[[\gamma _{ab}]]^{\mathcal {M},[i],g}\left ( [[\alpha _{a}]]^{\mathcal {M},[i],g}\right )$
if
$\lbrack \lbrack \gamma _{ab}\alpha _{a}]]^{\mathcal {M},[i],g}=[[\gamma _{ab}]]^{\mathcal {M},[i],g}\left ( [[\alpha _{a}]]^{\mathcal {M},[i],g}\right )$
if
 $[[\alpha _{a}]]^{\mathcal {M},[i],g}\not =\divideontimes $
, otherwise
$[[\alpha _{a}]]^{\mathcal {M},[i],g}\not =\divideontimes $
, otherwise
 $ [[\gamma _{ab}\alpha _{a}]]^{\mathcal {M},[i],g}=F_{b}$
.
$ [[\gamma _{ab}\alpha _{a}]]^{\mathcal {M},[i],g}=F_{b}$
.-
• Suppose
 $[[\alpha _{a}]]^{\mathcal {M},[i],g}$
is defined (
$[[\alpha _{a}]]^{\mathcal {M},[i],g}$
is defined (
 $ \not =\divideontimes $
). By the induction hypothesis
$ \not =\divideontimes $
). By the induction hypothesis
 $[[\gamma _{ab}]]^{ \mathcal {M},[i],g}=\Phi (@_{i}(\gamma _{ab})^{\widehat {g}})$
and
$[[\gamma _{ab}]]^{ \mathcal {M},[i],g}=\Phi (@_{i}(\gamma _{ab})^{\widehat {g}})$
and
 $[[\alpha _{a}]]^{\mathcal {M},[i],g}=\Phi (@_{i}(\alpha _{a})^{\widehat {g}})$
. Moreover, by semantical definition of function application as well as the definition of
$[[\alpha _{a}]]^{\mathcal {M},[i],g}=\Phi (@_{i}(\alpha _{a})^{\widehat {g}})$
. Moreover, by semantical definition of function application as well as the definition of
 $\Phi $
,
$\Phi $
,
 $\lbrack \lbrack \gamma _{ab}]]^{\mathcal {M},[i],g}\left ( [[\alpha _{a}]]^{ \mathcal {M},[i],g}\right ) =\Phi (@_{i_{n}}(@_{i}(\gamma _{ab})^{\widehat {g} })(@_{i}(\alpha _{a})^{\widehat {g}}))$
. It is easy to see that
$\lbrack \lbrack \gamma _{ab}]]^{\mathcal {M},[i],g}\left ( [[\alpha _{a}]]^{ \mathcal {M},[i],g}\right ) =\Phi (@_{i_{n}}(@_{i}(\gamma _{ab})^{\widehat {g} })(@_{i}(\alpha _{a})^{\widehat {g}}))$
. It is easy to see that
 $\Phi (@_{i_{n}}(@_{i}(\gamma _{ab})^{\widehat {g}})(@_{i}(\alpha _{a})^{ \widehat {g}}))=\Phi (@_{i}(\gamma _{ab}\alpha _{a})^{\widehat {g}})$
, as
$\Phi (@_{i_{n}}(@_{i}(\gamma _{ab})^{\widehat {g}})(@_{i}(\alpha _{a})^{ \widehat {g}}))=\Phi (@_{i}(\gamma _{ab}\alpha _{a})^{\widehat {g}})$
, as
 $\Gamma ^{\ast }\vdash @_{i_{n}}(@_{i}(\gamma _{ab})^{\widehat {g} })(@_{i}(\alpha _{a})^{\widehat {g}})\equiv @_{i}(\gamma _{ab}\alpha _{a})^{ \widehat {g}}$
. We use that
$\Gamma ^{\ast }\vdash @_{i_{n}}(@_{i}(\gamma _{ab})^{\widehat {g} })(@_{i}(\alpha _{a})^{\widehat {g}})\equiv @_{i}(\gamma _{ab}\alpha _{a})^{ \widehat {g}}$
. We use that
 $\Gamma ^{\ast }\vdash \mathsf {DEN}(@_{i}(\alpha _{a})^{ \widehat {g}})$
and
$\Gamma ^{\ast }\vdash \mathsf {DEN}(@_{i}(\alpha _{a})^{ \widehat {g}})$
and
 $\Gamma ^{\ast }\vdash \mathsf {DEN}(@_{i}(\gamma _{ab})^{\widehat {g}})$
as well as Proposition 6.3 items (2b) and (2d), Axioms 5b and 8b, and Proposition 6.3(1b). Since b is of
$\Gamma ^{\ast }\vdash \mathsf {DEN}(@_{i}(\gamma _{ab})^{\widehat {g}})$
as well as Proposition 6.3 items (2b) and (2d), Axioms 5b and 8b, and Proposition 6.3(1b). Since b is of
 $\mathsf {KIND}_{t}$
and both denote we can use condition (3) of Figure 2 of the definition of
$\mathsf {KIND}_{t}$
and both denote we can use condition (3) of Figure 2 of the definition of
 $\Phi $
. Thus,
$\Phi $
. Thus,
 $[[\gamma _{ab}\alpha _{a}]]^{\mathcal {M},[i],g}=\Phi (@_{i}(\gamma _{ab}\alpha _{a})^{\widehat {g}})$
, as required.
$[[\gamma _{ab}\alpha _{a}]]^{\mathcal {M},[i],g}=\Phi (@_{i}(\gamma _{ab}\alpha _{a})^{\widehat {g}})$
, as required. -
• So next suppose that
 $[[\alpha _{a}]]^{\mathcal {M},[i],g}$
is undefined (
$[[\alpha _{a}]]^{\mathcal {M},[i],g}$
is undefined (
 $=\divideontimes $
). By the induction hypothesis,
$=\divideontimes $
). By the induction hypothesis,
 $\Phi (@_{i}(\alpha _{a})^{\widehat {g}})=\divideontimes $
, so by condition (2) of Figure 2,
$\Phi (@_{i}(\alpha _{a})^{\widehat {g}})=\divideontimes $
, so by condition (2) of Figure 2,
 $\Gamma ^{\ast }\vdash \lnot \mathsf {DEN }(@_{i}(\alpha _{a})^{\widehat {g}})$
. Hence, by Axiom 8f,
$\Gamma ^{\ast }\vdash \lnot \mathsf {DEN }(@_{i}(\alpha _{a})^{\widehat {g}})$
. Hence, by Axiom 8f,
 $\Gamma ^{\ast }\vdash @_{i}(\gamma _{ab})^{\widehat {g}}(@_{i}(\alpha _{a})^{ \widehat {g}})\equiv \bot _{b}$
. And then
$\Gamma ^{\ast }\vdash @_{i}(\gamma _{ab})^{\widehat {g}}(@_{i}(\alpha _{a})^{ \widehat {g}})\equiv \bot _{b}$
. And then
 $\Gamma ^{\ast }\vdash @_{i}(\gamma _{ab}\alpha _{a})^{\widehat {g} }\equiv \bot _{b}$
(using Axioms 5b and 8b as well as Proposition 6.3(1b)). Since b is of
$\Gamma ^{\ast }\vdash @_{i}(\gamma _{ab}\alpha _{a})^{\widehat {g} }\equiv \bot _{b}$
(using Axioms 5b and 8b as well as Proposition 6.3(1b)). Since b is of
 $\mathsf {KIND}_{t}$
, both expressions denote, and we can apply condition (3) of Figure 2 to obtain
$\mathsf {KIND}_{t}$
, both expressions denote, and we can apply condition (3) of Figure 2 to obtain
 $\Phi (@_{i}(\gamma _{ab}\alpha _{a})^{\widehat {g}}))=\Phi (\bot _{b})=F_{b}$
, as required.
$\Phi (@_{i}(\gamma _{ab}\alpha _{a})^{\widehat {g}}))=\Phi (\bot _{b})=F_{b}$
, as required.
-
-
(3)
 $\lambda $
-expressions: We treat
$\lambda $
-expressions: We treat
 $\left \langle b,a\right \rangle \in \mathsf {KIND}_{e}$
and
$\left \langle b,a\right \rangle \in \mathsf {KIND}_{e}$
and
 $\left \langle b,a\right \rangle \in \mathsf {KIND}_{t}$
separately.
$\left \langle b,a\right \rangle \in \mathsf {KIND}_{t}$
separately.Let
 $\left \langle b,a\right \rangle \in \mathsf {KIND}_{e}$
. We need to show that
$\left \langle b,a\right \rangle \in \mathsf {KIND}_{e}$
. We need to show that
 $[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{ \mathcal {M},[i],g}=\Phi (@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})$
. Note that in
$[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{ \mathcal {M},[i],g}=\Phi (@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})$
. Note that in
 $\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}}$
the variable
$\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}}$
the variable
 $u_{b}$
is not free and so, it is not substituted when indicating
$u_{b}$
is not free and so, it is not substituted when indicating
 $\widehat {g}$
. We need to prove that both functions agree on any argument
$\widehat {g}$
. We need to prove that both functions agree on any argument
 $\Phi (\beta _{b})\in \mathsf {D}_{b}$
. By definition of
$\Phi (\beta _{b})\in \mathsf {D}_{b}$
. By definition of
 $\Phi $
, we have
$\Phi $
, we have
 $\Phi (@_{i}(\left \langle \lambda u_{b}\alpha _{a}\right \rangle )^{\widehat {g }})(\Phi (\beta _{b}))=\Phi (@_{i_{n}}(@_{i}\langle \lambda u_{b}\alpha _{a}^{\widehat {g}}\rangle )\beta _{b})$
. On the other hand, by semantical definition:
$\Phi (@_{i}(\left \langle \lambda u_{b}\alpha _{a}\right \rangle )^{\widehat {g }})(\Phi (\beta _{b}))=\Phi (@_{i_{n}}(@_{i}\langle \lambda u_{b}\alpha _{a}^{\widehat {g}}\rangle )\beta _{b})$
. On the other hand, by semantical definition:
 $[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M} ,[i],g}(\Phi (\beta _{b}))$
=
$[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M} ,[i],g}(\Phi (\beta _{b}))$
=
 $\left \{ \begin {array}{ll} \lbrack \lbrack \alpha _{a}]]^{\mathcal {M},[i],g_{u_{b}}^{\Phi (\beta _{b})}},& \text {if }\Phi (\beta _{b})\in \mathsf {D}_{b}^{[i]}, \\ \divideontimes \, , &\text {if }\Phi (\beta _{b})\in \mathsf {D}_{b}-\mathsf {D} _{b}^{[i]}. \end {array} \right. $
$\left \{ \begin {array}{ll} \lbrack \lbrack \alpha _{a}]]^{\mathcal {M},[i],g_{u_{b}}^{\Phi (\beta _{b})}},& \text {if }\Phi (\beta _{b})\in \mathsf {D}_{b}^{[i]}, \\ \divideontimes \, , &\text {if }\Phi (\beta _{b})\in \mathsf {D}_{b}-\mathsf {D} _{b}^{[i]}. \end {array} \right. $
We distinguish two cases, depending on whether (i)
 $\Phi (\beta _{b})\in \mathsf {D}_{b}^{[i]}$
or (ii)
$\Phi (\beta _{b})\in \mathsf {D}_{b}^{[i]}$
or (ii)
 $\Phi (\beta _{b})\in \mathsf {D}_{b}-\mathsf {D} _{b}^{[i]}$
.
$\Phi (\beta _{b})\in \mathsf {D}_{b}-\mathsf {D} _{b}^{[i]}$
.Case
 $(i)$
.
$(i)$
.
 $\Phi (\beta _{b})\in \mathsf {D}_{b}^{[i]}$
, then:
$\Phi (\beta _{b})\in \mathsf {D}_{b}^{[i]}$
, then:
 $[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M} ,[i],g}(\Phi (\beta _{b}))=[[\alpha _{a}]]^{\mathcal {M},[i],g_{u_{b}}^{\Phi (\beta _{b})}}=[[\alpha _{a}\frac {\beta _{b}}{u_{b}}]]^{\mathcal {M},[i],g}$
(by using substitution Lemma 4.7 and that
$[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M} ,[i],g}(\Phi (\beta _{b}))=[[\alpha _{a}]]^{\mathcal {M},[i],g_{u_{b}}^{\Phi (\beta _{b})}}=[[\alpha _{a}\frac {\beta _{b}}{u_{b}}]]^{\mathcal {M},[i],g}$
(by using substitution Lemma 4.7 and that
 $ g_{u_{b}}^{\Phi (\beta _{b})}(u_{b})=\Phi (\beta _{b})=\Phi (@_{i}\beta _{b})=[[\beta _{a}]]^{\mathcal {M},[i],g}$
(by induction hypothesis)
$ g_{u_{b}}^{\Phi (\beta _{b})}(u_{b})=\Phi (\beta _{b})=\Phi (@_{i}\beta _{b})=[[\beta _{a}]]^{\mathcal {M},[i],g}$
(by induction hypothesis)
 $=\Phi (@_{i}(\alpha _{a}\frac {\beta _{b}}{u_{b}})^{\widehat {g}})$
(by induction hypothesis on
$=\Phi (@_{i}(\alpha _{a}\frac {\beta _{b}}{u_{b}})^{\widehat {g}})$
(by induction hypothesis on
 $\alpha _{a}\frac {\beta _{b}}{u_{b}}$
)
$\alpha _{a}\frac {\beta _{b}}{u_{b}}$
)
 $=\Phi (@_{i}(\alpha _{a}^{\widehat {g}}\frac {\beta _{b}}{u_{b}}))$
(because of Remark 10.2 the variable
$=\Phi (@_{i}(\alpha _{a}^{\widehat {g}}\frac {\beta _{b}}{u_{b}}))$
(because of Remark 10.2 the variable
 $u_{b}$
is not replaced when a formula is linked with
$u_{b}$
is not replaced when a formula is linked with
 $\widehat {g}$
in this proof). Thus, we need to prove
$\widehat {g}$
in this proof). Thus, we need to prove
 $\Phi (@_{i_{n}}(@_{i}\langle \lambda u_{b}\alpha _{a}^{\widehat {g}}\rangle )\beta _{b})=\Phi (@_{i}(\alpha _{a}^{ \widehat {g}}\frac {\beta _{b}}{u_{b}}))$
, which is equivalent to
$\Phi (@_{i_{n}}(@_{i}\langle \lambda u_{b}\alpha _{a}^{\widehat {g}}\rangle )\beta _{b})=\Phi (@_{i}(\alpha _{a}^{ \widehat {g}}\frac {\beta _{b}}{u_{b}}))$
, which is equivalent to
 $\Gamma ^{\ast }\vdash @_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})\beta _{b}\equiv @_{i}(\alpha _{a})^{ \widehat {g}}\frac {\beta _{b}}{u_{b}}$
. Now, we have to consider two subcases: (i.1)
$\Gamma ^{\ast }\vdash @_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})\beta _{b}\equiv @_{i}(\alpha _{a})^{ \widehat {g}}\frac {\beta _{b}}{u_{b}}$
. Now, we have to consider two subcases: (i.1)
 $\Gamma ^{\ast }\vdash \mathsf {DEN}(@_{i_{n}}(@_{i}\langle \lambda u_{b}\alpha _{a}^{\widehat {g}}\rangle )\beta _{b})$
or (i.2)
$\Gamma ^{\ast }\vdash \mathsf {DEN}(@_{i_{n}}(@_{i}\langle \lambda u_{b}\alpha _{a}^{\widehat {g}}\rangle )\beta _{b})$
or (i.2)
 $\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(@_{i_{n}}(@_{i}\langle \lambda u_{b}\alpha _{a}^{\widehat {g}}\rangle )\beta _{b})$
.
$\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(@_{i_{n}}(@_{i}\langle \lambda u_{b}\alpha _{a}^{\widehat {g}}\rangle )\beta _{b})$
.Subcase (i.1). We have that
 $\Gamma ^{\ast }\vdash @_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat { g}})\beta _{b}\equiv (@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})\beta _{b}$
, because we already know that both expressions are weekly equals, the left expression denotes and so we can apply Proposition 6.3(1b). Therefore, what we need to prove now is:
$\Gamma ^{\ast }\vdash @_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat { g}})\beta _{b}\equiv (@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})\beta _{b}$
, because we already know that both expressions are weekly equals, the left expression denotes and so we can apply Proposition 6.3(1b). Therefore, what we need to prove now is:
 $\Gamma ^{\ast }\vdash (@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})\beta _{b}\equiv @_{i}(\alpha _{a})^{ \widehat {g}}\frac {\beta _{b}}{u_{b}}$
. By condition (2) in Figure 2 we have
$\Gamma ^{\ast }\vdash (@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})\beta _{b}\equiv @_{i}(\alpha _{a})^{ \widehat {g}}\frac {\beta _{b}}{u_{b}}$
. By condition (2) in Figure 2 we have
 $\Phi (@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g} })(\Phi (\beta _{b}))\not =\divideontimes $
. In the first place, by Axioms 10 and 1c, the Gen
$\Phi (@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g} })(\Phi (\beta _{b}))\not =\divideontimes $
. In the first place, by Axioms 10 and 1c, the Gen
 $_{@}$
Rule, and Proposition 6.3(2f), we have:
$_{@}$
Rule, and Proposition 6.3(2f), we have:
 $\vdash @_{i}(\mathsf {EXISTS}(\beta _{b}))\rightarrow @_{i}(\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g} }(\beta _{b}))\simeq @_{i}(\alpha _{a})^{\widehat {g}}\frac {\beta _{b}}{u_{b}}$
(where
$\vdash @_{i}(\mathsf {EXISTS}(\beta _{b}))\rightarrow @_{i}(\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g} }(\beta _{b}))\simeq @_{i}(\alpha _{a})^{\widehat {g}}\frac {\beta _{b}}{u_{b}}$
(where
 $\beta _{b}\in \mathsf {RIGIDS}$
and
$\beta _{b}\in \mathsf {RIGIDS}$
and
 $b\in \mathsf {KIND}_{e}$
). Moreover, as
$b\in \mathsf {KIND}_{e}$
). Moreover, as
 $\Phi (\beta _{b})\in \mathsf {D}_{b}^{[i]}$
, we have that
$\Phi (\beta _{b})\in \mathsf {D}_{b}^{[i]}$
, we have that
 $ \Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\beta _{b}))$
, and so
$ \Gamma ^{\ast }\vdash @_{i}(\mathsf {EXISTS}(\beta _{b}))$
, and so
 $\Gamma ^{\ast }\vdash @_{i}(\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}}(\beta _{b}))\simeq @_{i}(\alpha _{a})^{ \widehat {g}}\frac {\beta _{b}}{u_{b}}$
. As we already mentioned, the expression on the left could be simplified and so
$\Gamma ^{\ast }\vdash @_{i}(\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}}(\beta _{b}))\simeq @_{i}(\alpha _{a})^{ \widehat {g}}\frac {\beta _{b}}{u_{b}}$
. As we already mentioned, the expression on the left could be simplified and so
 $\Gamma ^{\ast }\vdash (@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})\beta _{b}\simeq @_{i}(\alpha _{a})^{ \widehat {g}}\frac {\beta _{b}}{u_{b}}$
and using the properties of
$\Gamma ^{\ast }\vdash (@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})\beta _{b}\simeq @_{i}(\alpha _{a})^{ \widehat {g}}\frac {\beta _{b}}{u_{b}}$
and using the properties of
 $\Phi $
and the fact that
$\Phi $
and the fact that
 $\Gamma ^{\ast }\vdash \mathsf {DEN}((@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g} })\beta _{b})$
(because we are in case (i.1) and both formulas are equivalent) we have:
$\Gamma ^{\ast }\vdash \mathsf {DEN}((@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g} })\beta _{b})$
(because we are in case (i.1) and both formulas are equivalent) we have:
 $\Gamma ^{\ast }\vdash (@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})\beta _{b}\equiv @_{i}(\alpha _{a})^{ \widehat {g}}\frac {\beta _{b}}{u_{b}}$
, as required.
$\Gamma ^{\ast }\vdash (@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})\beta _{b}\equiv @_{i}(\alpha _{a})^{ \widehat {g}}\frac {\beta _{b}}{u_{b}}$
, as required.Subcase (i.2). In this case, by condition (2) in Figure 2 we have that
 $\Phi ((@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})\beta _{b}))=\divideontimes $
.
$\Phi ((@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})\beta _{b}))=\divideontimes $
.However,
 $\Phi ((@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})\beta _{b}))=\Phi (@_{i_{n}}@_{i}(\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{ \widehat {g}}\beta _{b}))$
, as
$\Phi ((@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})\beta _{b}))=\Phi (@_{i_{n}}@_{i}(\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{ \widehat {g}}\beta _{b}))$
, as
 $\Gamma ^{\ast }\vdash @_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})\beta _{b}\simeq @_{i_{n}}@_{i}(\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat { g}}\beta _{b})$
. Hence by the induction hypothesis,
$\Gamma ^{\ast }\vdash @_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})\beta _{b}\simeq @_{i_{n}}@_{i}(\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat { g}}\beta _{b})$
. Hence by the induction hypothesis,
 $[[@_{i_{n}}@_{i}(\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}}\beta _{b})]]^{ \mathcal {M},[i_{n}],g}=\divideontimes $
.
$[[@_{i_{n}}@_{i}(\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}}\beta _{b})]]^{ \mathcal {M},[i_{n}],g}=\divideontimes $
.And so,
 $[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g} }\beta _{b}]]^{\mathcal {M},[i],g}=\divideontimes =[[(\alpha _{a})^{\widehat {g }}]]^{\mathcal {M},[i],g_{u_{b}}^{\Phi (\beta _{b})}}$
.
$[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g} }\beta _{b}]]^{\mathcal {M},[i],g}=\divideontimes =[[(\alpha _{a})^{\widehat {g }}]]^{\mathcal {M},[i],g_{u_{b}}^{\Phi (\beta _{b})}}$
.Case
 $(ii)$
. In the second case
$(ii)$
. In the second case
 $\Phi (\beta _{b})\in \mathsf {D}_{b}-\mathsf {D}_{b}^{[i]}$
, thus
$\Phi (\beta _{b})\in \mathsf {D}_{b}-\mathsf {D}_{b}^{[i]}$
, thus
 $\Gamma ^{\ast }\vdash \lnot @_{i}(\mathsf {EXISTS}(\beta _{b}))$
and by definition we have that
$\Gamma ^{\ast }\vdash \lnot @_{i}(\mathsf {EXISTS}(\beta _{b}))$
and by definition we have that
 $ [[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M} ,[i],g}(\Phi (\beta _{b}))=\divideontimes .$
We want to prove that
$ [[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M} ,[i],g}(\Phi (\beta _{b}))=\divideontimes .$
We want to prove that
 $\Phi (@_{i}\langle \lambda u_{b}\alpha _{a}\rangle ^{\widehat {g}})(\Phi (\beta _{b}))=\divideontimes $
as well. Using Axioms 11c and 1c and the Gen
$\Phi (@_{i}\langle \lambda u_{b}\alpha _{a}\rangle ^{\widehat {g}})(\Phi (\beta _{b}))=\divideontimes $
as well. Using Axioms 11c and 1c and the Gen
 $ _{@}$
Rule we have (
$ _{@}$
Rule we have (
 $b\in \mathsf {KIND}_{e}$
) that:
$b\in \mathsf {KIND}_{e}$
) that: $\vdash (@_{i}(\mathsf {EXISTS}{\small (}(@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}}))))\wedge @_{i}(\mathsf { \ DEN}((@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}}))\beta _{b})\rightarrow @_{i}(\mathsf {EXISTS }(\beta _{b})))$
. By Axiom 9a, the Gen
$\vdash (@_{i}(\mathsf {EXISTS}{\small (}(@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}}))))\wedge @_{i}(\mathsf { \ DEN}((@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}}))\beta _{b})\rightarrow @_{i}(\mathsf {EXISTS }(\beta _{b})))$
. By Axiom 9a, the Gen
 $_{@}$
Rule, and Axioms 3d, 11a, and 5b, we get
$_{@}$
Rule, and Axioms 3d, 11a, and 5b, we get
 $\vdash @_{i}(\mathsf {EXISTS}{\small (}(@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})))$
. Now, using the properties of maximal consistency and the fact that
$\vdash @_{i}(\mathsf {EXISTS}{\small (}(@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})))$
. Now, using the properties of maximal consistency and the fact that
 $\Gamma ^{\ast }\vdash \lnot @_{i}\mathsf {EXISTS}(\beta _{b})$
we get
$\Gamma ^{\ast }\vdash \lnot @_{i}\mathsf {EXISTS}(\beta _{b})$
we get
 $\Gamma ^{\ast }\vdash \lnot @_{i}(\mathsf {DEN}(@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})\beta _{b}))$
. So by Proposition 6.3(1e) and Axiom 3d,
$\Gamma ^{\ast }\vdash \lnot @_{i}(\mathsf {DEN}(@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})\beta _{b}))$
. So by Proposition 6.3(1e) and Axiom 3d,
 $\Gamma ^{\ast } \vdash \lnot \mathsf {DEN}(@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle )^{\widehat {g}}\beta _{b})$
. Then, by condition (2) in Figure 2:
$\Gamma ^{\ast } \vdash \lnot \mathsf {DEN}(@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle )^{\widehat {g}}\beta _{b})$
. Then, by condition (2) in Figure 2:
 $\divideontimes =\Phi ((@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})\beta _{b}))=\Phi (@_{i}(\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})(\Phi (\beta _{b}))$
.
$\divideontimes =\Phi ((@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})\beta _{b}))=\Phi (@_{i}(\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})(\Phi (\beta _{b}))$
.Let
 $\left \langle b,a\right \rangle \in \mathsf {KIND}_{t}$
. We need to show that
$\left \langle b,a\right \rangle \in \mathsf {KIND}_{t}$
. We need to show that
 $[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{ \mathcal {M},[i],g}\kern1.2pt{=}\kern1.2pt\Phi (@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})$
, that is, that both functions give the same value to every argument, say
$[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{ \mathcal {M},[i],g}\kern1.2pt{=}\kern1.2pt\Phi (@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})$
, that is, that both functions give the same value to every argument, say
 $\Phi (\beta _{b})$
. By definition of
$\Phi (\beta _{b})$
. By definition of
 $\Phi $
,
$\Phi $
,
 $\Phi (@_{i}(\left \langle \lambda u_{b}\alpha _{a}\right \rangle )^{\widehat {g }})(\Phi (\beta _{b}))=$
$\Phi (@_{i}(\left \langle \lambda u_{b}\alpha _{a}\right \rangle )^{\widehat {g }})(\Phi (\beta _{b}))=$
 $=\left \{ \begin {array}{l@{\ \,}l} \Phi ((@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle )^{ \widehat {g}})\beta _{b}), & \text {if }\Gamma ^{\ast }\nvdash (@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle )^{ \widehat {g}})\beta _{b})\equiv \bot _{a}, \\ \Phi ((@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle )^{ \widehat {g}})\beta _{b})=F_{a}, & \text {if }\Gamma ^{\ast }\vdash (@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle )^{ \widehat {g}})\beta _{b})\equiv \bot _{a}. \end {array} \right. $
On the other hand, by semantical definition,
$=\left \{ \begin {array}{l@{\ \,}l} \Phi ((@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle )^{ \widehat {g}})\beta _{b}), & \text {if }\Gamma ^{\ast }\nvdash (@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle )^{ \widehat {g}})\beta _{b})\equiv \bot _{a}, \\ \Phi ((@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle )^{ \widehat {g}})\beta _{b})=F_{a}, & \text {if }\Gamma ^{\ast }\vdash (@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle )^{ \widehat {g}})\beta _{b})\equiv \bot _{a}. \end {array} \right. $
On the other hand, by semantical definition,
 $[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M} ,[i],g}(\Phi (\beta _{b}))$
=
$[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M} ,[i],g}(\Phi (\beta _{b}))$
=
 $\left \{ \begin {array}{ll} \lbrack \lbrack \alpha _{a}]]^{\mathcal {M},[i],g_{u_{b}}^{\Phi (\beta _{b})}},& \text {if }\Phi (\beta _{b})\in \mathsf {D}_{b}^{[i]}, \\ F_{a} \, , &\text {if }\Phi (\beta _{b})\in \mathsf {D}_{b}-\mathsf {D}_{b}^{[i]}. \end {array} \right. $
We distinguish two cases, depending on whether (i)
$\left \{ \begin {array}{ll} \lbrack \lbrack \alpha _{a}]]^{\mathcal {M},[i],g_{u_{b}}^{\Phi (\beta _{b})}},& \text {if }\Phi (\beta _{b})\in \mathsf {D}_{b}^{[i]}, \\ F_{a} \, , &\text {if }\Phi (\beta _{b})\in \mathsf {D}_{b}-\mathsf {D}_{b}^{[i]}. \end {array} \right. $
We distinguish two cases, depending on whether (i)
 $\Phi (\beta _{b})\in \mathsf {\ D}_{b}^{[i]}$
or (ii)
$\Phi (\beta _{b})\in \mathsf {\ D}_{b}^{[i]}$
or (ii)
 $\Phi (\beta _{b})\in \mathsf {D}_{b}-\mathsf {D}_{b}^{[i]}$
.
$\Phi (\beta _{b})\in \mathsf {D}_{b}-\mathsf {D}_{b}^{[i]}$
.Case (i). In the first case
 $\Phi (\beta _{b})\in \mathsf {D}_{b}^{[i]}$
, by semantical definition and induction hypothesis, we have that
$\Phi (\beta _{b})\in \mathsf {D}_{b}^{[i]}$
, by semantical definition and induction hypothesis, we have that
 $[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M},[i],g}(\Phi (\beta _{b}))=[[\alpha _{a}]]^{ \mathcal {M},[i],g_{u_{b}}^{\Phi (\beta _{b})}}=\Phi (@_{i}(\alpha _{a})^{ \widehat {g_{u_{b}}^{\Phi (\beta _{b})}}})$
. To arrive to the desired conclusion, we have to prove that
$[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M},[i],g}(\Phi (\beta _{b}))=[[\alpha _{a}]]^{ \mathcal {M},[i],g_{u_{b}}^{\Phi (\beta _{b})}}=\Phi (@_{i}(\alpha _{a})^{ \widehat {g_{u_{b}}^{\Phi (\beta _{b})}}})$
. To arrive to the desired conclusion, we have to prove that
 $\Gamma ^{\ast }\vdash @_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle )^{ \widehat {g}})\beta _{b}\equiv @_{i}(\alpha _{a})^{\widehat {g}}\frac {\beta _{b}}{u_{b}}$
. By Proposition 6.3(2e), Axiom 1c, and the Gen
$\Gamma ^{\ast }\vdash @_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle )^{ \widehat {g}})\beta _{b}\equiv @_{i}(\alpha _{a})^{\widehat {g}}\frac {\beta _{b}}{u_{b}}$
. By Proposition 6.3(2e), Axiom 1c, and the Gen
 $_{@}$
Rule (for
$_{@}$
Rule (for
 $\beta _{b}\in \mathsf {RIGIDS }$
and
$\beta _{b}\in \mathsf {RIGIDS }$
and
 $a\in \mathsf {KIND}_{t}$
) we have that
$a\in \mathsf {KIND}_{t}$
) we have that
 $\vdash @_{i}( \mathsf {EXISTS}(\beta _{b}))\rightarrow @_{i}(\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}}(\beta ))\equiv @_{i}(\alpha _{a})^{\widehat {g}}\frac {\beta _{b}}{u_{b}}$
and due to
$\vdash @_{i}( \mathsf {EXISTS}(\beta _{b}))\rightarrow @_{i}(\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}}(\beta ))\equiv @_{i}(\alpha _{a})^{\widehat {g}}\frac {\beta _{b}}{u_{b}}$
and due to
 $\Phi (\beta _{b})\in \mathsf {D}_{b}^{[i]}$
, we also have
$\Phi (\beta _{b})\in \mathsf {D}_{b}^{[i]}$
, we also have
 $\Gamma ^{\ast }\vdash @_{i}( \mathsf {EXISTS}(\beta _{b}))$
, and so
$\Gamma ^{\ast }\vdash @_{i}( \mathsf {EXISTS}(\beta _{b}))$
, and so
 $\Gamma ^{\ast }\vdash @_{i}(\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g} }(\beta ))\equiv @_{i}(\alpha _{a})^{\widehat {g}}\frac {\beta _{b}}{u_{b}}$
. We get
$\Gamma ^{\ast }\vdash @_{i}(\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g} }(\beta ))\equiv @_{i}(\alpha _{a})^{\widehat {g}}\frac {\beta _{b}}{u_{b}}$
. We get
 $\Gamma ^{\ast }\vdash @_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle )^{\widehat {g}})\beta _{b}\equiv @_{i}(\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g} }(\beta ))$
, by Proposition 6.3 items 2b, 2c, and 2d. So at the final step we obtain
$\Gamma ^{\ast }\vdash @_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle )^{\widehat {g}})\beta _{b}\equiv @_{i}(\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g} }(\beta ))$
, by Proposition 6.3 items 2b, 2c, and 2d. So at the final step we obtain
 $\Phi (@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle )^{ \widehat {g}})\beta _{b})=\Phi (@_{i}(\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}}(\beta )))=\Phi (@_{i}(\alpha _{a})^{ \widehat {g}}\frac {\beta _{b}}{u_{b}})=\Phi (@_{i}(\alpha _{a})^{\widehat { g_{u_{b}}^{\Phi (\beta _{b})}}})$
. This follows by property (3) of the definition of
$\Phi (@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle )^{ \widehat {g}})\beta _{b})=\Phi (@_{i}(\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}}(\beta )))=\Phi (@_{i}(\alpha _{a})^{ \widehat {g}}\frac {\beta _{b}}{u_{b}})=\Phi (@_{i}(\alpha _{a})^{\widehat { g_{u_{b}}^{\Phi (\beta _{b})}}})$
. This follows by property (3) of the definition of
 $\Phi $
(recall Figure 2).
$\Phi $
(recall Figure 2).Case
 $(ii)$
.
$(ii)$
.
 $\Phi (\beta _{b})\in \mathsf {D}_{b}-\mathsf {D} _{b}^{[i]}$
, thus
$\Phi (\beta _{b})\in \mathsf {D}_{b}-\mathsf {D} _{b}^{[i]}$
, thus
 $\Gamma ^{\ast }\vdash \lnot @_{i}(\mathsf {EXISTS}(\beta _{b}))$
, and by semantical definition we have that
$\Gamma ^{\ast }\vdash \lnot @_{i}(\mathsf {EXISTS}(\beta _{b}))$
, and by semantical definition we have that
 $[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M},[i],g}(\Phi (\beta _{b}))=F_{a}$
. We want to prove that
$[[\left \langle \lambda u_{b}\alpha _{a}\right \rangle ]]^{\mathcal {M},[i],g}(\Phi (\beta _{b}))=F_{a}$
. We want to prove that
 $\Phi (@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})(\Phi (\beta _{b}))=F_{a}$
as well. To arrive to this conclusion we will prove that
$\Phi (@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})(\Phi (\beta _{b}))=F_{a}$
as well. To arrive to this conclusion we will prove that
 $\Gamma ^{\ast }\vdash (@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle )^{ \widehat {g}})\beta _{b})\equiv \bot _{a}$
. By Axiom 11d, the Gen
$\Gamma ^{\ast }\vdash (@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle )^{ \widehat {g}})\beta _{b})\equiv \bot _{a}$
. By Axiom 11d, the Gen
 $_{@}$
Rule, and Axioms 1c and 3b) we have that
$_{@}$
Rule, and Axioms 1c and 3b) we have that
 $\vdash (@_{i}(\mathsf {EXISTS}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}}))\kern1.2pt{\wedge}\kern1.2pt \lnot ((@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})\kern1.2pt{\equiv}\kern1.2pt \bot _{a}))\kern1.2pt{\rightarrow}\kern1.2pt @_{i}(\mathsf {EXISTS}(\beta _{b}))$
, then we obtain
$\vdash (@_{i}(\mathsf {EXISTS}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}}))\kern1.2pt{\wedge}\kern1.2pt \lnot ((@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})\kern1.2pt{\equiv}\kern1.2pt \bot _{a}))\kern1.2pt{\rightarrow}\kern1.2pt @_{i}(\mathsf {EXISTS}(\beta _{b}))$
, then we obtain
 $\Gamma ^{\ast }\vdash \lnot (@_{i}(\mathsf {EXISTS}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}}))\vee ((@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g} })\equiv \bot _{a}))$
. However, by Axiom 9a, Rule 2c, Axioms 3d, 11a, and 5b, we obtain
$\Gamma ^{\ast }\vdash \lnot (@_{i}(\mathsf {EXISTS}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}}))\vee ((@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g} })\equiv \bot _{a}))$
. However, by Axiom 9a, Rule 2c, Axioms 3d, 11a, and 5b, we obtain
 $\vdash @_{i}(\mathsf {EXISTS}{\small (}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}}))$
, and so finally we get
$\vdash @_{i}(\mathsf {EXISTS}{\small (}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}}))$
, and so finally we get
 $\Gamma ^{\ast }\vdash (@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})\equiv \bot _{a}$
. Hence, using Axiom 3d and the properties of maximal consistent sets, we have
$\Gamma ^{\ast }\vdash (@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle ^{\widehat {g}})\equiv \bot _{a}$
. Hence, using Axiom 3d and the properties of maximal consistent sets, we have
 $\Gamma ^{\ast }\vdash (@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle )^{ \widehat {g}})\beta _{b})\equiv \bot _{a}$
, as we wanted to prove.
$\Gamma ^{\ast }\vdash (@_{i_{n}}(@_{i}\left \langle \lambda u_{b}\alpha _{a}\right \rangle )^{ \widehat {g}})\beta _{b})\equiv \bot _{a}$
, as we wanted to prove.
Corollary 10.4. Let
![]() $\mathcal {M}$
be the structure induced by a named,
$\mathcal {M}$
be the structure induced by a named,
![]() $\Diamond $
-saturated,
$\Diamond $
-saturated,
![]() $\exists $
-saturated, and
$\exists $
-saturated, and
![]() $\mathsf {E}$
-saturated maximal consistent set, and let g be any assignment function on
$\mathsf {E}$
-saturated maximal consistent set, and let g be any assignment function on
![]() $\mathcal {M}$
. Then
$\mathcal {M}$
. Then
![]() $\langle \mathcal {M},g \rangle $
is a general interpretation.
$\langle \mathcal {M},g \rangle $
is a general interpretation.
Corollary 10.5. For each
![]() $\alpha _a\in \mathsf {CME}_a$
and any
$\alpha _a\in \mathsf {CME}_a$
and any
![]() $i \in \mathsf {NOM}\ [[ \alpha _a]]^{\mathcal {M},[i],g}=\Phi (@_i\alpha _a)$
.
$i \in \mathsf {NOM}\ [[ \alpha _a]]^{\mathcal {M},[i],g}=\Phi (@_i\alpha _a)$
.
Theorem 10.6 (Henkin’s theorem).
Every consistent set of sentences has a general interpretation that satisfies it.
Proof Standard.
Theorem 10.7 (Completeness).
For all
![]() $\Gamma \subseteq \mathsf {CME}_t$
and
$\Gamma \subseteq \mathsf {CME}_t$
and
![]() $\varphi \in \mathsf {CME}_t $
, the following holds:
$\varphi \in \mathsf {CME}_t $
, the following holds:
![]() $\Gamma \models \varphi $
implies
$\Gamma \models \varphi $
implies
![]() $\Gamma \vdash \varphi .$
$\Gamma \vdash \varphi .$
Proof Standard.
11 Concluding remarks
In this article we defined a system called
![]() $\mathcal {HPTT}$
, a combination of William Farmer’s partial type theory and a strong form of hybrid logic; our goal was to investigate varying domain semantics in the setting of higher-order modal logic. In higher-order settings, there are several plausible ways of defining local domains, and in this paper we explored the following idea: A function is local to a world w if it is only defined on elements of w. When defining the different levels of our hierarchy we demand, at each level, the union of the local universes be the global universe of that level. In
$\mathcal {HPTT}$
, a combination of William Farmer’s partial type theory and a strong form of hybrid logic; our goal was to investigate varying domain semantics in the setting of higher-order modal logic. In higher-order settings, there are several plausible ways of defining local domains, and in this paper we explored the following idea: A function is local to a world w if it is only defined on elements of w. When defining the different levels of our hierarchy we demand, at each level, the union of the local universes be the global universe of that level. In
![]() $\mathcal {HPTT}$
two fundamental notions play a relevant role, those of “denotation” and “existence,”
$\mathcal {HPTT}$
two fundamental notions play a relevant role, those of “denotation” and “existence,”
![]() $\mathsf {DEN}$
and
$\mathsf {DEN}$
and
![]() $\mathsf {EXISTS}$
. They are defined by using the lambda abstractor as well as the hybrid
$\mathsf {EXISTS}$
. They are defined by using the lambda abstractor as well as the hybrid
![]() ${\downarrow }$
and
${\downarrow }$
and
![]() $\mathsf {A}$
operators. In our system,
$\mathsf {A}$
operators. In our system,
![]() $\mathsf {DEN}$
definition reflects the choice we have made in defining the structures we wanted to talk about, where anything that denotes must reside in at least one local quantification domain; we do not allow what we called a “Phantom zone” (see [Reference Blackburn, Martins, Manzano and Huertas7]). In this system, the formula
$\mathsf {DEN}$
definition reflects the choice we have made in defining the structures we wanted to talk about, where anything that denotes must reside in at least one local quantification domain; we do not allow what we called a “Phantom zone” (see [Reference Blackburn, Martins, Manzano and Huertas7]). In this system, the formula
![]() $ \mathsf {DEN}(\alpha _{a}) \equiv (\alpha _{a} \equiv \alpha _{a})$
is valid but in a different system where the union of the local universes were allowed to be proper subsets of the global universes, this formula is no longer valid. Defining denotation by
$ \mathsf {DEN}(\alpha _{a}) \equiv (\alpha _{a} \equiv \alpha _{a})$
is valid but in a different system where the union of the local universes were allowed to be proper subsets of the global universes, this formula is no longer valid. Defining denotation by
![]() $\alpha _{a} \equiv \alpha _{a}$
will simplify the logical system by eliminating
$\alpha _{a} \equiv \alpha _{a}$
will simplify the logical system by eliminating
![]() ${\downarrow }$
and
${\downarrow }$
and
![]() $\mathsf {A}$
; however, in this case it opens the door to phantom zones and does not reflect the choice we have made,
$\mathsf {A}$
; however, in this case it opens the door to phantom zones and does not reflect the choice we have made,
![]() $\bigcup _{w \in W} \mathsf {D}_{a}^{w} = \mathsf {D}_{a}$
. In a future work, hybrid partial type theory systems with phantom zones could be investigated.
$\bigcup _{w \in W} \mathsf {D}_{a}^{w} = \mathsf {D}_{a}$
. In a future work, hybrid partial type theory systems with phantom zones could be investigated.
We proved a strong completeness result for the basic logic—and here we remark that by using standard results from hybrid logic, the result can be extended to completeness theorems for many different frame conditions, and many different modal logics (e.g., multimodal logic, tense logic, and D-logic); detailed discussion and proofs can be found in [Reference Blackburn, Huertas, Manzano, Jørgensen, Manzano, Sain and Alonso6].
To conclude this paper, we briefly discuss the broader motivations for our work. Several completeness results in higher-order modal logic have been motivated by linguistic or philosophical issues. For example, Gallins’ [Reference Gallin15] PhD thesis, one of the earliest completeness results in this area, proved a completeness result for Montague’s IL, a higher-order logic which played a key role in the development of natural language semantics. More recently, Fitting [Reference Fitting13] replaces function/argument syntax with predicate/argument syntax in his investigation of Gödel’s version of the ontological argument, and provides a complete tableau system.
The work reported here belongs to this tradition. We believe higher-order hybrid logic provides a useful tool for investigating many linguistic and philosophical issues, that varying domain semantics is important to these issues, and that a better understanding of partiality will be required for such investigations. On the linguistic side, we believe that higher-order hybrid tense logic provides a framework in which the key ideas tracing back to Richard Montague, Arthur Prior, Hans Reichenbach, and Leon Henkin can be made to work together smoothly (see [Reference Areces, Blackburn, Manzano and Huertas3] for more discussion). However, as well as issues relevant to temporal semantic, we believe that
![]() $\mathcal {HPTT}$
also provides an arena in which many classical issues in the semantics of modality can be usefully addressed (see [Reference Aranda, Huertas, Manzano and Martins1]). The completeness theorem proved in this paper provides a technical foundation for this ongoing work.
$\mathcal {HPTT}$
also provides an arena in which many classical issues in the semantics of modality can be usefully addressed (see [Reference Aranda, Huertas, Manzano and Martins1]). The completeness theorem proved in this paper provides a technical foundation for this ongoing work.
12 Appendix: proofs of some theorems
12.1 Proof of Proposition 6.2
-
6.2(1) Proof of
 $\vdash @_{i}\varphi \rightarrow \mathsf {E} \varphi $
:
$\vdash @_{i}\varphi \rightarrow \mathsf {E} \varphi $
:-
 $\vdash @_{h} \mathsf {E}i \wedge @_{i} \varphi \rightarrow @_{h} \mathsf {E} \varphi $
, by Bridge
$\vdash @_{h} \mathsf {E}i \wedge @_{i} \varphi \rightarrow @_{h} \mathsf {E} \varphi $
, by Bridge
 $_{\mathsf {E}}$
.
$_{\mathsf {E}}$
. -
 $\vdash @_{h} \mathsf {E}i \rightarrow (@_{i} \varphi \rightarrow @_{h} \mathsf {E} \varphi )$
, by tautologies.
$\vdash @_{h} \mathsf {E}i \rightarrow (@_{i} \varphi \rightarrow @_{h} \mathsf {E} \varphi )$
, by tautologies. -
 $\vdash \mathsf {E}i$
, by Axiom 6a.
$\vdash \mathsf {E}i$
, by Axiom 6a. -
 $\vdash @_{h} \mathsf {E}i$
, by Rule 2c.
$\vdash @_{h} \mathsf {E}i$
, by Rule 2c. -
 $\vdash @_{i} \varphi \rightarrow @_{h} \mathsf {E} \varphi $
, by Modus Ponens, 6 and 8.
$\vdash @_{i} \varphi \rightarrow @_{h} \mathsf {E} \varphi $
, by Modus Ponens, 6 and 8. -
 $\vdash @_{h} \mathsf {E} \varphi \rightarrow \mathsf {E} \varphi $
, by Axiom 6a and
$\vdash @_{h} \mathsf {E} \varphi \rightarrow \mathsf {E} \varphi $
, by Axiom 6a and
 $\equiv $
definition.
$\equiv $
definition. -
 $\vdash @_{i} \varphi \rightarrow \mathsf {E} \varphi $
, by transitivity, 5 and 6.
$\vdash @_{i} \varphi \rightarrow \mathsf {E} \varphi $
, by transitivity, 5 and 6.
-
-
6.2(2) Proof of
 $\vdash @_{i}(\varphi \rightarrow \psi )\equiv (@_{i}\varphi \rightarrow @_{i}\psi ) $
: The left-to-right direction is the Distributivity Axiom 1c. The right-to-left direction follows from Distributivity Axiom 1c by classical tautologies and Axiom 3b.
$\vdash @_{i}(\varphi \rightarrow \psi )\equiv (@_{i}\varphi \rightarrow @_{i}\psi ) $
: The left-to-right direction is the Distributivity Axiom 1c. The right-to-left direction follows from Distributivity Axiom 1c by classical tautologies and Axiom 3b. -
6.2(3) Proof of
 $\vdash \varphi \rightarrow \mathsf {E}\varphi $
:
$\vdash \varphi \rightarrow \mathsf {E}\varphi $
:-
 $\vdash @_{i} \varphi \rightarrow \mathsf {E} \varphi $
, by Proposition 6.2(1) (with
$\vdash @_{i} \varphi \rightarrow \mathsf {E} \varphi $
, by Proposition 6.2(1) (with
 $i \in \mathsf {NOM}$
does not occur in
$i \in \mathsf {NOM}$
does not occur in
 $ \varphi $
).
$ \varphi $
). -
 $\vdash @_{i} (@_{i} \varphi \rightarrow \mathsf {E} \varphi )$
, by Rule 2c.
$\vdash @_{i} (@_{i} \varphi \rightarrow \mathsf {E} \varphi )$
, by Rule 2c. -
 $\vdash @_{i} @_{i} \varphi \rightarrow @_{i} \mathsf {E} \varphi $
, by Axiom 1c.
$\vdash @_{i} @_{i} \varphi \rightarrow @_{i} \mathsf {E} \varphi $
, by Axiom 1c. -
 $\vdash @_{i} \varphi \rightarrow @_{i} \mathsf {E} \varphi $
, by Axiom 3d.
$\vdash @_{i} \varphi \rightarrow @_{i} \mathsf {E} \varphi $
, by Axiom 3d. -
 $\vdash @_{i} (\varphi \rightarrow \mathsf {E} \varphi )$
, by Proposition 6.2(2).
$\vdash @_{i} (\varphi \rightarrow \mathsf {E} \varphi )$
, by Proposition 6.2(2). -
 $\vdash \varphi \rightarrow \mathsf {E} \varphi $
, by Name
$\vdash \varphi \rightarrow \mathsf {E} \varphi $
, by Name
 $^{\prime }$
.
$^{\prime }$
.
-
-
6.2(4) Proof of
 $\vdash \mathsf {E}\varphi \rightarrow \mathsf {A}\mathsf {E}\varphi $
: It follows from Axiom 6b (with
$\vdash \mathsf {E}\varphi \rightarrow \mathsf {A}\mathsf {E}\varphi $
: It follows from Axiom 6b (with
 $i \in \mathsf {NOM}$
does not occur in
$i \in \mathsf {NOM}$
does not occur in
 $\varphi $
), Axioms 2b and 2c, 3b, Back
$\varphi $
), Axioms 2b and 2c, 3b, Back
 $_{\mathsf {E}}$
, 3d, Proposition 6.2(2), and Name
$_{\mathsf {E}}$
, 3d, Proposition 6.2(2), and Name
 $^{\prime }$
.
$^{\prime }$
. -
6.2(5) Proof of
 $\vdash \varphi \rightarrow \mathsf {A} \mathsf {E}\varphi $
: It follows by transitivity from Proposition 6.2(3) and Proposition 6.2(4).
$\vdash \varphi \rightarrow \mathsf {A} \mathsf {E}\varphi $
: It follows by transitivity from Proposition 6.2(3) and Proposition 6.2(4). -
6.2(6) Proof of
 $\vdash \Diamond \varphi \rightarrow \mathsf {E}\varphi $
:
$\vdash \Diamond \varphi \rightarrow \mathsf {E}\varphi $
:-
 $\vdash @_{i} \neg \varphi \rightarrow \neg \varphi $
, by Name
$\vdash @_{i} \neg \varphi \rightarrow \neg \varphi $
, by Name
 $^{\prime }$
(with
$^{\prime }$
(with
 $i \in \mathsf {NOM}$
does not occur in
$i \in \mathsf {NOM}$
does not occur in
 $\varphi $
).
$\varphi $
). -
 $\vdash \Box (@_{i} \neg \varphi \rightarrow \neg \varphi )$
, by Rule 2a.
$\vdash \Box (@_{i} \neg \varphi \rightarrow \neg \varphi )$
, by Rule 2a. -
 $\vdash \Box @_{i} \neg \varphi \rightarrow \Box \neg \varphi $
, by Axiom 1a.
$\vdash \Box @_{i} \neg \varphi \rightarrow \Box \neg \varphi $
, by Axiom 1a. -
 $\vdash \Diamond \neg @_{i} \neg \varphi \lor \neg \Diamond \varphi $
, by
$\vdash \Diamond \neg @_{i} \neg \varphi \lor \neg \Diamond \varphi $
, by
 $\Box $
and
$\Box $
and
 $\rightarrow $
definitions.
$\rightarrow $
definitions. -
 $\vdash \Diamond @_{i} \varphi \lor \neg \Diamond \varphi $
, by Axiom 3b.
$\vdash \Diamond @_{i} \varphi \lor \neg \Diamond \varphi $
, by Axiom 3b. -
 $\vdash \Diamond \varphi \rightarrow \Diamond @_{i} \varphi $
, by tautologies and
$\vdash \Diamond \varphi \rightarrow \Diamond @_{i} \varphi $
, by tautologies and
 $\rightarrow $
definition.
$\rightarrow $
definition. -
 $\vdash \Diamond @_{i} \varphi \rightarrow @_{i} \varphi $
, by Back
$\vdash \Diamond @_{i} \varphi \rightarrow @_{i} \varphi $
, by Back
 $_{\Diamond }$
.
$_{\Diamond }$
. -
 $\vdash \Diamond \varphi \rightarrow @_{i} \varphi $
, by transitivity 6 and 7.
$\vdash \Diamond \varphi \rightarrow @_{i} \varphi $
, by transitivity 6 and 7. -
 $\vdash @_{i} \varphi \rightarrow \mathsf {E} \varphi $
, by Proposition 6.2(1).
$\vdash @_{i} \varphi \rightarrow \mathsf {E} \varphi $
, by Proposition 6.2(1). -
 $\vdash \Diamond \varphi \rightarrow \mathsf {E} \varphi $
, by transitivity 8 and 9.
$\vdash \Diamond \varphi \rightarrow \mathsf {E} \varphi $
, by transitivity 8 and 9.
-
-
6.2(7) Proof of
 $\vdash \mathsf {E} h\equiv @_{h^{\prime }} \mathsf {E}h$
: It is a particular case of Axiom 6b.
$\vdash \mathsf {E} h\equiv @_{h^{\prime }} \mathsf {E}h$
: It is a particular case of Axiom 6b.
12.2 Proof of Proposition 6.3
We sketch the ideas needed to construct the required proofs.
-
6.3(1a) Proof of
 $\vdash \mathsf {DEN}(\alpha _{a}) \equiv (\alpha _{a} \equiv \alpha _{a})$
: The left-right direction follows from Axiom 4a, Definition 5.1, and classical propositional logic, while the right-left direction is a direct consequence of Axiom 8e.
$\vdash \mathsf {DEN}(\alpha _{a}) \equiv (\alpha _{a} \equiv \alpha _{a})$
: The left-right direction follows from Axiom 4a, Definition 5.1, and classical propositional logic, while the right-left direction is a direct consequence of Axiom 8e. -
6.3(1b) Proof of
 $\vdash \mathsf {DEN}(\alpha )\rightarrow ((\alpha \simeq \beta )\equiv (\alpha \equiv \beta ))$
: It is a direct consequence of the definition of
$\vdash \mathsf {DEN}(\alpha )\rightarrow ((\alpha \simeq \beta )\equiv (\alpha \equiv \beta ))$
: It is a direct consequence of the definition of
 $\alpha _{a}\simeq \beta _{a}$
.
$\alpha _{a}\simeq \beta _{a}$
. -
6.3(1c) Proof of
 $\vdash \mathsf {DEN}(@_{h}\alpha _{a})\equiv @_{h}\mathsf {DEN}(\alpha _{a})$
: It follows immediately from Proposition 6.3(1a) and Axiom 5a.
$\vdash \mathsf {DEN}(@_{h}\alpha _{a})\equiv @_{h}\mathsf {DEN}(\alpha _{a})$
: It follows immediately from Proposition 6.3(1a) and Axiom 5a. -
6.3(1d) Proof of
 $\vdash (\mathsf {DEN} (\alpha _{a})\wedge \alpha _{a}\simeq \beta _{a})\rightarrow \mathsf {DEN} (\beta _{a})$
: It follows directly from Denotation Axiom 8e by using classical propositional rules as well as the definition of
$\vdash (\mathsf {DEN} (\alpha _{a})\wedge \alpha _{a}\simeq \beta _{a})\rightarrow \mathsf {DEN} (\beta _{a})$
: It follows directly from Denotation Axiom 8e by using classical propositional rules as well as the definition of
 $\simeq $
.
$\simeq $
. -
6.3(1e) Proof of
 $\vdash \mathsf {DEN}(\alpha _{a})\equiv \mathsf {DEN}(@_{i}\alpha _{a})$
,
$\vdash \mathsf {DEN}(\alpha _{a})\equiv \mathsf {DEN}(@_{i}\alpha _{a})$
,
 $\alpha _{a}\in \mathsf {RIGIDS}$
as well as
$\alpha _{a}\in \mathsf {RIGIDS}$
as well as
 $\vdash \mathsf {DEN}(\alpha _{a})\equiv @_{i}\mathsf {DEN}(\alpha _{a})$
,
$\vdash \mathsf {DEN}(\alpha _{a})\equiv @_{i}\mathsf {DEN}(\alpha _{a})$
,
 $\alpha _{a}\in \mathsf {RIGIDS}$
. To prove both theorems we proceed as follows:
$\alpha _{a}\in \mathsf {RIGIDS}$
. To prove both theorems we proceed as follows: $\vdash (\mathsf {DEN}(\alpha _{a})\wedge \alpha _{a}\simeq @_{i}\alpha _{a})\rightarrow \mathsf {DEN}(@_{i}\alpha _{a})$
, by Proposition 6.3(1d).
$\vdash (\mathsf {DEN}(\alpha _{a})\wedge \alpha _{a}\simeq @_{i}\alpha _{a})\rightarrow \mathsf {DEN}(@_{i}\alpha _{a})$
, by Proposition 6.3(1d). $\vdash (\mathsf {DEN}(@_{i}\alpha _{a})\wedge @_{i}\alpha _{a}\simeq \alpha _{a})\rightarrow \mathsf {DEN}(\alpha _{a})$
, by Proposition 6.3(1d).
$\vdash (\mathsf {DEN}(@_{i}\alpha _{a})\wedge @_{i}\alpha _{a}\simeq \alpha _{a})\rightarrow \mathsf {DEN}(\alpha _{a})$
, by Proposition 6.3(1d). $\vdash @_{i}\alpha _{a}\simeq \alpha _{a}$
, by Rigids are rigid (Axiom 3d).
$\vdash @_{i}\alpha _{a}\simeq \alpha _{a}$
, by Rigids are rigid (Axiom 3d). $\vdash \alpha _{a}\simeq @_{i}\alpha _{a}$
, by Symmetry (Axiom 4b) and Modus Ponens.
$\vdash \alpha _{a}\simeq @_{i}\alpha _{a}$
, by Symmetry (Axiom 4b) and Modus Ponens. $\vdash \mathsf {DEN}(\alpha _{a})\equiv \mathsf {DEN}(@_{i}\alpha _{a})$
, by classical propositional logic.
$\vdash \mathsf {DEN}(\alpha _{a})\equiv \mathsf {DEN}(@_{i}\alpha _{a})$
, by classical propositional logic.To prove
 $\vdash \mathsf {DEN}(\alpha _{a})\equiv @_{i}\mathsf {DEN}(\alpha _{a})$
,
$\vdash \mathsf {DEN}(\alpha _{a})\equiv @_{i}\mathsf {DEN}(\alpha _{a})$
,
 $\alpha _{a}\in \mathsf {RIGIDS}$
we use Proposition 6.3(1c).
$\alpha _{a}\in \mathsf {RIGIDS}$
we use Proposition 6.3(1c). -
6.3(1f) Proof of
 $\vdash \mathsf {DEN(}@_{h}(\gamma _{ab}\alpha _{a}))\rightarrow @_{h}(\gamma _{ab}\alpha _{a})\equiv (@_{h}\gamma _{ab}\alpha _{a}))$
, for
$\vdash \mathsf {DEN(}@_{h}(\gamma _{ab}\alpha _{a}))\rightarrow @_{h}(\gamma _{ab}\alpha _{a})\equiv (@_{h}\gamma _{ab}\alpha _{a}))$
, for
 $\alpha _{a}\in \mathsf {RIGIDS}$
:
$\alpha _{a}\in \mathsf {RIGIDS}$
:-
 $\vdash @_{h}\alpha _{a}\simeq \alpha _{a}$
, by Rigids are rigid (Axiom 3d).
$\vdash @_{h}\alpha _{a}\simeq \alpha _{a}$
, by Rigids are rigid (Axiom 3d). -
 $\vdash @_{h}(\gamma _{ab}\alpha _{a})\simeq (@_{h}(\gamma _{ab})(@_{h}\alpha _{a}))$
, by Axiom 5b.
$\vdash @_{h}(\gamma _{ab}\alpha _{a})\simeq (@_{h}(\gamma _{ab})(@_{h}\alpha _{a}))$
, by Axiom 5b. -
 $\vdash (@_{h}(\gamma _{ab})(@_{h}\alpha _{a}))\simeq (@_{h}(\gamma _{ab})\alpha _{a})$
, by Functional schema 11a and first line.
$\vdash (@_{h}(\gamma _{ab})(@_{h}\alpha _{a}))\simeq (@_{h}(\gamma _{ab})\alpha _{a})$
, by Functional schema 11a and first line. -
 $\vdash @_{h}(\gamma _{ab}\alpha _{a})\simeq (@_{h}(\gamma _{ab})\alpha _{a}) $
, by Equality schemas on previous lines.
$\vdash @_{h}(\gamma _{ab}\alpha _{a})\simeq (@_{h}(\gamma _{ab})\alpha _{a}) $
, by Equality schemas on previous lines. -
 $\vdash \mathsf {DEN(}@_{h}(\gamma _{ab}\alpha _{a}))\rightarrow @_{h}(\gamma _{ab}\alpha _{a})\equiv (@_{h}\gamma _{ab})\alpha _{a}))$
, by Proposition 6.3(1b)) and previous line.
$\vdash \mathsf {DEN(}@_{h}(\gamma _{ab}\alpha _{a}))\rightarrow @_{h}(\gamma _{ab}\alpha _{a})\equiv (@_{h}\gamma _{ab})\alpha _{a}))$
, by Proposition 6.3(1b)) and previous line.
-
-
6.3(3a) The proof of
 $\vdash \mathsf {DEN}(\alpha _{a})\equiv \mathsf { E(EXIST}(\alpha _{a}))$
, with
$\vdash \mathsf {DEN}(\alpha _{a})\equiv \mathsf { E(EXIST}(\alpha _{a}))$
, with
 $\alpha _{a}\in \mathsf {RIGIDS}$
is divided into two directions:
$\alpha _{a}\in \mathsf {RIGIDS}$
is divided into two directions:-
• The left-right direction,
 $\vdash \mathsf {DEN}(\alpha _{a})\rightarrow \mathsf {E}(\mathsf {EXISTS} (\alpha _{a}))$
,
$\vdash \mathsf {DEN}(\alpha _{a})\rightarrow \mathsf {E}(\mathsf {EXISTS} (\alpha _{a}))$
,
 $\alpha _{a}\in \mathsf {RIGIDS}$
, follows from three logical theorems:
$\alpha _{a}\in \mathsf {RIGIDS}$
, follows from three logical theorems:-
(a)
 $\mathsf {DEN}$
for rigids: 6.3(1e)
$\mathsf {DEN}$
for rigids: 6.3(1e)
 $ \vdash \mathsf {DEN}(\alpha _{a})\equiv \mathsf {DEN}(@_{i}\alpha _{a})$
,
$ \vdash \mathsf {DEN}(\alpha _{a})\equiv \mathsf {DEN}(@_{i}\alpha _{a})$
,
 $ \alpha _{a}\in \mathsf {RIGIDS}$
as well as
$ \alpha _{a}\in \mathsf {RIGIDS}$
as well as
 $\vdash \mathsf {DEN}(\alpha _{a})\equiv @_{i}\mathsf {DEN}(\alpha _{a})$
,
$\vdash \mathsf {DEN}(\alpha _{a})\equiv @_{i}\mathsf {DEN}(\alpha _{a})$
,
 $ \alpha _{a}\in \mathsf {RIGIDS}$
.
$ \alpha _{a}\in \mathsf {RIGIDS}$
. -
(b)
 $\mathsf {DEN}$
at
$\mathsf {DEN}$
at
 $\mathbf {i}$
-world:
$\mathbf {i}$
-world:
 $\vdash @_{i} \mathsf {DEN}(\alpha _{a})\rightarrow \mathsf {E}(\mathsf {EXISTS}(@_{i}\alpha _{a}))$
.
$\vdash @_{i} \mathsf {DEN}(\alpha _{a})\rightarrow \mathsf {E}(\mathsf {EXISTS}(@_{i}\alpha _{a}))$
. -
(c)
 $\mathsf {EXISTS}$
somewhere for rigids:
$\mathsf {EXISTS}$
somewhere for rigids:
 $\vdash \mathsf { E(EXISTS}(\alpha _{a}))\equiv \mathsf {\ E(EXISTS}(@_{i}\alpha _{a}))$
, for
$\vdash \mathsf { E(EXISTS}(\alpha _{a}))\equiv \mathsf {\ E(EXISTS}(@_{i}\alpha _{a}))$
, for
 $ \alpha _{a}\in \mathsf {RIGIDS}.$
$ \alpha _{a}\in \mathsf {RIGIDS}.$
The first item is the previous Proposition 6.3(1e).The proof of the second item (
 $\mathsf {DEN}$
at
$\mathsf {DEN}$
at
 $\mathbf {i}$
-world) requires to apply Downarrow (Axiom 7) over the definition of denotation as well as Axiom 6b:
$\mathbf {i}$
-world) requires to apply Downarrow (Axiom 7) over the definition of denotation as well as Axiom 6b:-
 $\vdash @_{i}\mathsf {DEN}(\alpha _{a})\rightarrow @_{i}\mathsf {DEN}(\alpha _{a})$
, by propositional calculus.
$\vdash @_{i}\mathsf {DEN}(\alpha _{a})\rightarrow @_{i}\mathsf {DEN}(\alpha _{a})$
, by propositional calculus. -
By definition,
 $\mathsf {DEN}(\alpha _{a}):={{\downarrow \hspace {-0.1 pt}} }s(\mathsf {E}( \mathsf {EXISTS}(@_{s}\alpha _{a}))$
.
$\mathsf {DEN}(\alpha _{a}):={{\downarrow \hspace {-0.1 pt}} }s(\mathsf {E}( \mathsf {EXISTS}(@_{s}\alpha _{a}))$
. -
 $\vdash @_{i}\left ( {{\downarrow \hspace {-0.1 pt}} }s(\mathsf {E}(\mathsf {EXISTS}(@_{s}\alpha _{a})))\equiv \mathsf {E}(\mathsf {EXISTS}(@_{s}\alpha _{a}))(\frac {i}{s} )\right ) $
, by Axiom Downarrow 7.
$\vdash @_{i}\left ( {{\downarrow \hspace {-0.1 pt}} }s(\mathsf {E}(\mathsf {EXISTS}(@_{s}\alpha _{a})))\equiv \mathsf {E}(\mathsf {EXISTS}(@_{s}\alpha _{a}))(\frac {i}{s} )\right ) $
, by Axiom Downarrow 7. -
 $\vdash @_{i}({{\downarrow \hspace {-0.1 pt}} }s(\mathsf {E}(\mathsf {EXISTS}(@_{s}\alpha _{a}))))\equiv @_{i}(\mathsf {E}(\mathsf {EXISTS}(@_{s}\alpha _{a})))(\frac {i}{ s})$
, by Axiom 5a.
$\vdash @_{i}({{\downarrow \hspace {-0.1 pt}} }s(\mathsf {E}(\mathsf {EXISTS}(@_{s}\alpha _{a}))))\equiv @_{i}(\mathsf {E}(\mathsf {EXISTS}(@_{s}\alpha _{a})))(\frac {i}{ s})$
, by Axiom 5a. -
By definition of substitution,
 $@_{i}(\mathsf {E}(\mathsf {EXISTS}(@_{s}\alpha _{a}))(\frac {i}{s})):=@_{i}\mathsf {E}(\mathsf {EXISTS}(@_{i}\alpha _{a})).$
$@_{i}(\mathsf {E}(\mathsf {EXISTS}(@_{s}\alpha _{a}))(\frac {i}{s})):=@_{i}\mathsf {E}(\mathsf {EXISTS}(@_{i}\alpha _{a})).$
-
 $\vdash @_{i}\mathsf {DEN}(\alpha _{a})\rightarrow @_{i}(\mathsf {E}( \mathsf {EXISTS}(@_{i}\alpha _{a}))$
, from previous lines.
$\vdash @_{i}\mathsf {DEN}(\alpha _{a})\rightarrow @_{i}(\mathsf {E}( \mathsf {EXISTS}(@_{i}\alpha _{a}))$
, from previous lines. -
 $\vdash @_{i}\mathsf {DEN}(\alpha _{a})\rightarrow \mathsf {E}(\mathsf { EXISTS}(@_{i}\alpha _{a}))$
, by Axiom 6b.
$\vdash @_{i}\mathsf {DEN}(\alpha _{a})\rightarrow \mathsf {E}(\mathsf { EXISTS}(@_{i}\alpha _{a}))$
, by Axiom 6b.
The proof of the third item (
 $\mathsf {EXISTS}$
somewhere for rigids) only requires Proposition 6.3(2c) as well as Axiom 3d and Proposition 6.2(3).
$\mathsf {EXISTS}$
somewhere for rigids) only requires Proposition 6.3(2c) as well as Axiom 3d and Proposition 6.2(3). -
-
• Let’s go now for a proof to the right-left direction of our theorem,
 $\vdash \mathsf {E(EXISTS}(\alpha _{a}))\rightarrow \mathsf {DEN}(\alpha _{a})\text {, with }\alpha _{a}\in \mathsf {RIGIDS}$
:
$\vdash \mathsf {E(EXISTS}(\alpha _{a}))\rightarrow \mathsf {DEN}(\alpha _{a})\text {, with }\alpha _{a}\in \mathsf {RIGIDS}$
:-
 $\vdash @_{i}\mathsf {DEN}(\alpha _{a})\rightarrow @_{i}\mathsf {DEN} (\alpha _{a})$
, by propositional calculus.
$\vdash @_{i}\mathsf {DEN}(\alpha _{a})\rightarrow @_{i}\mathsf {DEN} (\alpha _{a})$
, by propositional calculus. -
 $\vdash @_{i}\mathsf {DEN}(\alpha _{a})\rightarrow \mathsf {DEN} (@_{i}\alpha _{a})$
, by Proposition 6.3(1c).
$\vdash @_{i}\mathsf {DEN}(\alpha _{a})\rightarrow \mathsf {DEN} (@_{i}\alpha _{a})$
, by Proposition 6.3(1c). -
 $\vdash @_{i}\mathsf {DEN}(\alpha _{a})\rightarrow \mathsf {DEN}(\alpha _{a})$
, by Proposition 6.3(1e) (with
$\vdash @_{i}\mathsf {DEN}(\alpha _{a})\rightarrow \mathsf {DEN}(\alpha _{a})$
, by Proposition 6.3(1e) (with
 $\alpha _{a}\in \mathsf {RIGIDS}$
).
$\alpha _{a}\in \mathsf {RIGIDS}$
). -
By def.
 $\mathsf {DEN}(\alpha _{a}):={{\downarrow \hspace {-0.1 pt}} }s(\mathsf {E}( \mathsf {EXISTS}(@_{s}\alpha _{a})).$
$\mathsf {DEN}(\alpha _{a}):={{\downarrow \hspace {-0.1 pt}} }s(\mathsf {E}( \mathsf {EXISTS}(@_{s}\alpha _{a})).$
-
 $\vdash @_{i}\left ( {{\downarrow \hspace {-0.1 pt}} }s(\mathsf {E}(\mathsf {EXISTS} (@_{s}\alpha _{a})))\equiv \mathsf {E}(\mathsf {EXISTS}(@_{s}\alpha _{a}))( \frac {i}{s})\right ) $
, by Downarrow Axiom 7.
$\vdash @_{i}\left ( {{\downarrow \hspace {-0.1 pt}} }s(\mathsf {E}(\mathsf {EXISTS} (@_{s}\alpha _{a})))\equiv \mathsf {E}(\mathsf {EXISTS}(@_{s}\alpha _{a}))( \frac {i}{s})\right ) $
, by Downarrow Axiom 7. -
 $\vdash @_{i}({{\downarrow \hspace {-0.1 pt}} }s(\mathsf {E}(\mathsf {EXISTS}(@_{s}\alpha _{a}))))\equiv @_{i}(\mathsf {E}(\mathsf {EXISTS}(@_{s}\alpha _{a})))(\frac {i}{ s})$
, by Axiom 5a.
$\vdash @_{i}({{\downarrow \hspace {-0.1 pt}} }s(\mathsf {E}(\mathsf {EXISTS}(@_{s}\alpha _{a}))))\equiv @_{i}(\mathsf {E}(\mathsf {EXISTS}(@_{s}\alpha _{a})))(\frac {i}{ s})$
, by Axiom 5a. -
By def. substitution,
 $@_{i}(\mathsf {E}(\mathsf {EXISTS}(@_{s}\alpha _{a}))(\frac {i}{s})):=@_{i}\mathsf {E}(\mathsf {EXISTS}(@_{i}\alpha _{a})).$
$@_{i}(\mathsf {E}(\mathsf {EXISTS}(@_{s}\alpha _{a}))(\frac {i}{s})):=@_{i}\mathsf {E}(\mathsf {EXISTS}(@_{i}\alpha _{a})).$
-
 $\vdash @_{i}\mathsf {E}(\mathsf {EXISTS}(@_{i}\alpha _{a}))\rightarrow \mathsf {DEN}(\alpha _{a})$
from previous lines.
$\vdash @_{i}\mathsf {E}(\mathsf {EXISTS}(@_{i}\alpha _{a}))\rightarrow \mathsf {DEN}(\alpha _{a})$
from previous lines. -
 $\vdash \mathsf {E}(\mathsf {EXISTS}(@_{i}\alpha _{a}))\rightarrow \mathsf {DEN}(\alpha _{a})$
, by Axiom 6b.
$\vdash \mathsf {E}(\mathsf {EXISTS}(@_{i}\alpha _{a}))\rightarrow \mathsf {DEN}(\alpha _{a})$
, by Axiom 6b. -
 $\vdash \mathsf {E}(\mathsf {EXISTS}(\alpha _{a}))\rightarrow \mathsf {DEN }(\alpha _{a})$
, with
$\vdash \mathsf {E}(\mathsf {EXISTS}(\alpha _{a}))\rightarrow \mathsf {DEN }(\alpha _{a})$
, with
 $\alpha _{a}\in \mathsf {RIGIDS}$
(as we saw previously).
$\alpha _{a}\in \mathsf {RIGIDS}$
(as we saw previously).
-
-
12.3 Proof of Lemma 8.1
Let
![]() $\Gamma ^\ast =\underset {n\in \omega }{\cup }\Gamma ^{n}$
. It is clear that
$\Gamma ^\ast =\underset {n\in \omega }{\cup }\Gamma ^{n}$
. It is clear that
![]() $\Gamma ^\ast $
is a named,
$\Gamma ^\ast $
is a named,
![]() $\Diamond $
-saturated,
$\Diamond $
-saturated,
![]() $\mathsf {E} $
-saturated, and
$\mathsf {E} $
-saturated, and
![]() $\exists $
-saturated: we added the nominal
$\exists $
-saturated: we added the nominal
![]() $i_{0}$
to
$i_{0}$
to
![]() $ \Gamma ^{0}$
at the very first step (hence it is named), and then inductively saturated all formulas prefixed by
$ \Gamma ^{0}$
at the very first step (hence it is named), and then inductively saturated all formulas prefixed by
![]() $\Diamond $
,
$\Diamond $
,
![]() $\exists $
and
$\exists $
and
![]() $\mathsf {E}$
. To show that
$\mathsf {E}$
. To show that
![]() $\Gamma ^\ast $
is also a maximal consistent set, we first show that for every
$\Gamma ^\ast $
is also a maximal consistent set, we first show that for every
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $\Gamma ^{n}$
is consistent.
$\Gamma ^{n}$
is consistent.
-
•
 $\Gamma ^{0}=\Gamma \cup \left \{ i_{0}\right \}$
is consistent. For suppose it is not. Then
$\Gamma ^{0}=\Gamma \cup \left \{ i_{0}\right \}$
is consistent. For suppose it is not. Then
 $\Gamma \cup \left \{ i_{0}\right \} \vdash \bot $
. Hence by the Deduction Theorem,
$\Gamma \cup \left \{ i_{0}\right \} \vdash \bot $
. Hence by the Deduction Theorem,
 $\Gamma \vdash \neg i_{0}$
. So for some finite conjunction
$\Gamma \vdash \neg i_{0}$
. So for some finite conjunction
 $\theta $
of formulas from
$\theta $
of formulas from
 $\Gamma $
, we have
$\Gamma $
, we have
 $\vdash \theta \rightarrow \neg i_{0}$
, and hence,
$\vdash \theta \rightarrow \neg i_{0}$
, and hence,
 $\vdash i_{0} \rightarrow \neg \theta $
. But as
$\vdash i_{0} \rightarrow \neg \theta $
. But as
 $i_{0}$
is new it does not occur in
$i_{0}$
is new it does not occur in
 $\Gamma $
, so we can apply the Name rule (page 12) and deduce that
$\Gamma $
, so we can apply the Name rule (page 12) and deduce that
 $\vdash \neg \theta $
, contradicting the consistency of
$\vdash \neg \theta $
, contradicting the consistency of
 $\Gamma $
. We conclude that
$\Gamma $
. We conclude that
 $\Gamma ^{0}=\Gamma \cup \left \{ i_{0}\right \}$
is consistent after all.
$\Gamma ^{0}=\Gamma \cup \left \{ i_{0}\right \}$
is consistent after all. -
• Assume
 $\Gamma ^{n}$
is consistent. The
$\Gamma ^{n}$
is consistent. The
 $\Gamma ^{n+1}$
is of one of the following forms:
$\Gamma ^{n+1}$
is of one of the following forms:-
i)
 $\Gamma ^{n+1}=\Gamma ^{n}$
. In this case it is consistent by the induction hypothesis.
$\Gamma ^{n+1}=\Gamma ^{n}$
. In this case it is consistent by the induction hypothesis. -
ii)
 $\Gamma ^{n+1}=\Gamma ^{n}\cup \left \{ \varphi _{n}\right \} $
. In this case it is consistent by definition.
$\Gamma ^{n+1}=\Gamma ^{n}\cup \left \{ \varphi _{n}\right \} $
. In this case it is consistent by definition. -
iii)
 $\Gamma ^{n+1}=\Gamma ^{n}\cup \{\varphi _{n},@_{i}\Diamond i_{m},@_{i_{m}}\psi \}$
, where
$\Gamma ^{n+1}=\Gamma ^{n}\cup \{\varphi _{n},@_{i}\Diamond i_{m},@_{i_{m}}\psi \}$
, where
 $\varphi _{n}:=@_{i}\Diamond \psi $
and
$\varphi _{n}:=@_{i}\Diamond \psi $
and
 $ i_{m} $
is the first new nominal that does not occur in
$ i_{m} $
is the first new nominal that does not occur in
 $\Gamma ^{n}$
or
$\Gamma ^{n}$
or
 $ \varphi _{n}$
. We know that
$ \varphi _{n}$
. We know that
 $\Gamma ^{n}\cup \{\varphi _{n}\}$
is consistent. We want to show that
$\Gamma ^{n}\cup \{\varphi _{n}\}$
is consistent. We want to show that
 $\Gamma ^{n}\cup \{\varphi _{n},@_{i}\Diamond i_{m},@_{i_{m}}\psi \}$
is consistent too. So suppose it is not. Then: Hence, by the Deduction Theorem,
$\Gamma ^{n}\cup \{\varphi _{n},@_{i}\Diamond i_{m},@_{i_{m}}\psi \}$
is consistent too. So suppose it is not. Then: Hence, by the Deduction Theorem, $$ \begin{align*} \Gamma ^{n}\cup \{\varphi _{n},@_{i}\Diamond i_{m},@_{i_{m}}\psi \}\vdash \bot. \end{align*} $$
$$ \begin{align*} \Gamma ^{n}\cup \{\varphi _{n},@_{i}\Diamond i_{m},@_{i_{m}}\psi \}\vdash \bot. \end{align*} $$
 $\Gamma ^{n}\cup \left \{ \varphi _{n}\right \} \vdash \lnot (@_{i}\Diamond i_{m}\wedge @_{i_{m}}\psi )$
, and so for some finite conjunction
$\Gamma ^{n}\cup \left \{ \varphi _{n}\right \} \vdash \lnot (@_{i}\Diamond i_{m}\wedge @_{i_{m}}\psi )$
, and so for some finite conjunction
 $\theta $
of formulas from
$\theta $
of formulas from
 $\Gamma ^{n}\cup \left \{ \varphi _{n}\right \} $
, we have
$\Gamma ^{n}\cup \left \{ \varphi _{n}\right \} $
, we have
 $\vdash \theta \rightarrow \lnot (@_{i}\Diamond i_{m}\wedge @_{i_{m}}\psi )$
, and hence,
$\vdash \theta \rightarrow \lnot (@_{i}\Diamond i_{m}\wedge @_{i_{m}}\psi )$
, and hence,
 $\vdash (@_{i}\Diamond i_{m}\wedge @_{i_{m}}\psi )\rightarrow \lnot \theta $
. But
$\vdash (@_{i}\Diamond i_{m}\wedge @_{i_{m}}\psi )\rightarrow \lnot \theta $
. But
 $ i_{m}$
is the first new nominal that does not occur in
$ i_{m}$
is the first new nominal that does not occur in
 $\Gamma ^{n}$
or
$\Gamma ^{n}$
or
 $ \varphi _{n}$
so we can apply the Paste
$ \varphi _{n}$
so we can apply the Paste
 $_{\Diamond }$
Rule (page 12) obtaining
$_{\Diamond }$
Rule (page 12) obtaining
 $\vdash @_{i}\Diamond \psi \rightarrow \lnot \theta $
and contradicting the consistency of
$\vdash @_{i}\Diamond \psi \rightarrow \lnot \theta $
and contradicting the consistency of
 $\Gamma ^{n}\cup \left \{ \varphi _{n}\right \}$
.
$\Gamma ^{n}\cup \left \{ \varphi _{n}\right \}$
.
-
iv)
 $\Gamma ^{n}\cup \{\varphi _{n},@_{i_{m}}\psi \}$
, where
$\Gamma ^{n}\cup \{\varphi _{n},@_{i_{m}}\psi \}$
, where
 $\varphi _{n}:=@_{i}\mathsf {E}\psi $
and
$\varphi _{n}:=@_{i}\mathsf {E}\psi $
and
 $i_{m}$
is the first nominal that does not occur in
$i_{m}$
is the first nominal that does not occur in
 $\Gamma ^{n}$
or
$\Gamma ^{n}$
or
 $\varphi _{n}$
. Consistency follows as in case (iii), but using the Paste
$\varphi _{n}$
. Consistency follows as in case (iii), but using the Paste
 $_{\mathsf {E}}$
(page 12) instead.
$_{\mathsf {E}}$
(page 12) instead. -
(v)
 $\Gamma ^{n}\cup \{\varphi _{n},@_{i}(\mathsf {EXISTS}(c_{m,a})),@_{i}\psi \frac {@_{i}c_{m,a}}{x_{a}}\}$
, where
$\Gamma ^{n}\cup \{\varphi _{n},@_{i}(\mathsf {EXISTS}(c_{m,a})),@_{i}\psi \frac {@_{i}c_{m,a}}{x_{a}}\}$
, where
 $\varphi _{n}:=@_{i}\exists x_{a}\psi $
and
$\varphi _{n}:=@_{i}\exists x_{a}\psi $
and
 $c_{m,a}$
is the first new constant of type a that does not occur in
$c_{m,a}$
is the first new constant of type a that does not occur in
 $\Gamma ^{n}$
or
$\Gamma ^{n}$
or
 $\varphi _{n}$
. Consistency follows as in case (iii), but using Paste
$\varphi _{n}$
. Consistency follows as in case (iii), but using Paste
 $_{\exists }$
(page 12) instead.
$_{\exists }$
(page 12) instead.
-
Thus, as we claimed above, for all
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $\Gamma ^{n}$
is consistent. But with this established it follows (by the standard argument) that
$\Gamma ^{n}$
is consistent. But with this established it follows (by the standard argument) that
![]() $\Gamma ^\ast =\underset {n\in \omega }{\bigcup }\Gamma ^{n}$
is both consistent and maximal. Hence
$\Gamma ^\ast =\underset {n\in \omega }{\bigcup }\Gamma ^{n}$
is both consistent and maximal. Hence
![]() $\Gamma ^\ast $
is the named,
$\Gamma ^\ast $
is the named,
![]() $\Diamond $
-saturated,
$\Diamond $
-saturated,
![]() $\exists $
-saturated,
$\exists $
-saturated,
![]() ${\mathsf {E}}$
-saturated, and maximal consistent set we were looking for.
${\mathsf {E}}$
-saturated, and maximal consistent set we were looking for.
12.4 Proof of some items from Theorem 10.3
-
(1) Nominals: Clearly
 $(j)^{ \widehat {g}}:=j$
. By the definition of
$(j)^{ \widehat {g}}:=j$
. By the definition of
 $\mathsf {I}$
,
$\mathsf {I}$
,
 $[[j]]^{\mathcal {M} ,[i],g}=\left [ \mathsf {I}(j)\right ] ([i])$
. By the definition of induced structure,
$[[j]]^{\mathcal {M} ,[i],g}=\left [ \mathsf {I}(j)\right ] ([i])$
. By the definition of induced structure,
 $\left [ \mathsf {I}(j)\right ] (\left [ i\right ] )=T$
iff
$\left [ \mathsf {I}(j)\right ] (\left [ i\right ] )=T$
iff
 $j\in \left [ i\right ]$
iff
$j\in \left [ i\right ]$
iff
 $i\in \left [ j\right ]$
iff
$i\in \left [ j\right ]$
iff
 $@_ij\in \Gamma ^\ast $
iff
$@_ij\in \Gamma ^\ast $
iff
 $ \Phi (@_ij)=\Phi (@_i(j)^{\widehat {g}})=T$
.
$ \Phi (@_ij)=\Phi (@_i(j)^{\widehat {g}})=T$
. -
(2) State variables:
 $[[s]]^{ \mathcal {M},[i],g}=T$
iff
$[[s]]^{ \mathcal {M},[i],g}=T$
iff
 $g(s)=\left [ i\right ] $
. By the previous definition,
$g(s)=\left [ i\right ] $
. By the previous definition,
 $(s)^{\widehat {g}}:=j$
, where j is the chosen representative of
$(s)^{\widehat {g}}:=j$
, where j is the chosen representative of
 $\left [ i\right ] $
. As they are equivalence classes,
$\left [ i\right ] $
. As they are equivalence classes,
 $\left [ i\right ] = \left [ j\right ]$
and so, by the definition of
$\left [ i\right ] = \left [ j\right ]$
and so, by the definition of
 $\Phi $
,
$\Phi $
,
 $\Phi (@_ij)=T$
iff
$\Phi (@_ij)=T$
iff
 $ @_ij\in \Gamma ^\ast $
iff
$ @_ij\in \Gamma ^\ast $
iff
 $i\in \left [ j\right ] $
. Therefore
$i\in \left [ j\right ] $
. Therefore
 $[[s]]^{ \mathcal {M},[i],g}=\Phi (@_i(s)^{\widehat {g}})$
.
$[[s]]^{ \mathcal {M},[i],g}=\Phi (@_i(s)^{\widehat {g}})$
. -
(3) Constants: Clearly
 $(c_b)^{ \widehat {g}}:=c_b$
. And then,
$(c_b)^{ \widehat {g}}:=c_b$
. And then, $[[c_b]]^{\mathcal {M},[i],g}=\left [ \mathsf {I}(c_b)\right ] ([i])=\left \{ \begin {array}{c} \Phi (@_ic_b)\text {, if }\mathsf {DEN}(@_ic_b)\in \Gamma ^\ast , \\ \divideontimes \text {, when }\mathsf {DEN}(@_ic_b)\not \in \Gamma ^\ast. \end {array} \right. $
$[[c_b]]^{\mathcal {M},[i],g}=\left [ \mathsf {I}(c_b)\right ] ([i])=\left \{ \begin {array}{c} \Phi (@_ic_b)\text {, if }\mathsf {DEN}(@_ic_b)\in \Gamma ^\ast , \\ \divideontimes \text {, when }\mathsf {DEN}(@_ic_b)\not \in \Gamma ^\ast. \end {array} \right. $
-
(4) Variables:
 $[[v_{b}]]^{\mathcal {M},[i],g}=g(v_{b})\in \mathsf {D}_{b}$
. By Lemma 9.16,
$[[v_{b}]]^{\mathcal {M},[i],g}=g(v_{b})\in \mathsf {D}_{b}$
. By Lemma 9.16,
 $g(v_{b})=\Phi (@_{j}c_{b})$
with
$g(v_{b})=\Phi (@_{j}c_{b})$
with
 $\mathsf {DEN}(@_{j}c_{b})\in \Gamma ^{\ast }$
, and assume that j and
$\mathsf {DEN}(@_{j}c_{b})\in \Gamma ^{\ast }$
, and assume that j and
 $c_{b}$
are the first nominal and constant with this property. By definition,
$c_{b}$
are the first nominal and constant with this property. By definition,
 $(v_{b})^{ \widehat {g}}:=@_{j}c_{b}$
. By Corollary 9.14,
$(v_{b})^{ \widehat {g}}:=@_{j}c_{b}$
. By Corollary 9.14,
 $\Phi (@_{j}c_{b})=\Phi (@_{i}@_{j}c_{b})$
and so
$\Phi (@_{j}c_{b})=\Phi (@_{i}@_{j}c_{b})$
and so
 $[[v_{b}]]^{\mathcal {M} ,[i],g}=\Phi (@_{i}(v_{b})^{\widehat {g}})$
.
$[[v_{b}]]^{\mathcal {M} ,[i],g}=\Phi (@_{i}(v_{b})^{\widehat {g}})$
. -
(5) Negations: By definition of
 $\Phi $
and induction hypothesis,
$\Phi $
and induction hypothesis,
 $[[\lnot \varphi ]]^{ \mathcal {M},[i],g}=T$
iff
$[[\lnot \varphi ]]^{ \mathcal {M},[i],g}=T$
iff
 $[[\varphi ]]^{\mathcal {M},[i],g}=F$
iff
$[[\varphi ]]^{\mathcal {M},[i],g}=F$
iff
 $ @_{i}(\varphi )^{\widehat {g}}\notin \Gamma ^{\ast }$
iff
$ @_{i}(\varphi )^{\widehat {g}}\notin \Gamma ^{\ast }$
iff
 $\lnot @_{i}(\varphi )^{\widehat {g}}\in \Gamma ^{\ast }$
iff
$\lnot @_{i}(\varphi )^{\widehat {g}}\in \Gamma ^{\ast }$
iff
 $@_{i}(\lnot \varphi )^{\widehat {g}}\in \Gamma ^{\ast }$
iff
$@_{i}(\lnot \varphi )^{\widehat {g}}\in \Gamma ^{\ast }$
iff
 $\Phi (@_{i}(\lnot \varphi )^{ \widehat {g}})=T.$
$\Phi (@_{i}(\lnot \varphi )^{ \widehat {g}})=T.$
-
(6) Conjunctions:
 $\varphi \wedge \psi \in \mathsf {ME}_{t}$
. The proof is straightforward.
$\varphi \wedge \psi \in \mathsf {ME}_{t}$
. The proof is straightforward. -
(7) @-Nominals: We will prove that
 $[[@_{j}\alpha _{a}]]^{\mathcal {M},[i],g}=\Phi (@_{i}(@_{j}\alpha _{a})^{\widehat {g}})$
. In the first place,
$[[@_{j}\alpha _{a}]]^{\mathcal {M},[i],g}=\Phi (@_{i}(@_{j}\alpha _{a})^{\widehat {g}})$
. In the first place,
 $[[@_{j}\alpha _{a}]]^{\mathcal {M},[i],g}=[[\alpha _{a}]]^{\mathcal {M},[j],g}$
(because
$[[@_{j}\alpha _{a}]]^{\mathcal {M},[i],g}=[[\alpha _{a}]]^{\mathcal {M},[j],g}$
(because
 $ [I(j)]([k])=T$
iff
$ [I(j)]([k])=T$
iff
 $j\in \lbrack k]$
iff
$j\in \lbrack k]$
iff
 $[k]=[j]$
). By the induction hypothesis,
$[k]=[j]$
). By the induction hypothesis,
 $[[\alpha _{a}]]^{\mathcal {M},[j],g}=\Phi ((@_{j}\alpha _{a})^{\widehat {g}})$
. By Corollary 9.14,
$[[\alpha _{a}]]^{\mathcal {M},[j],g}=\Phi ((@_{j}\alpha _{a})^{\widehat {g}})$
. By Corollary 9.14,
 $\Phi ((@_{j}\alpha _{a})^{\widehat {g}})=\Phi (@_{i}(@_{j}\alpha _{a})^{\widehat {g}}))$
, as required.
$\Phi ((@_{j}\alpha _{a})^{\widehat {g}})=\Phi (@_{i}(@_{j}\alpha _{a})^{\widehat {g}}))$
, as required. -
(8) @-State-Variables: We will prove that
 $[[@_{s}\alpha _{a}]]^{\mathcal {M},[i],g}=\Phi (@_{i}(@_{s}\alpha _{a})^{\widehat {g}})$
. We have that
$[[@_{s}\alpha _{a}]]^{\mathcal {M},[i],g}=\Phi (@_{i}(@_{s}\alpha _{a})^{\widehat {g}})$
. We have that
 $\lbrack \lbrack @_{s}\alpha _{a}]]^{\mathcal {M},[i],g}=[[\alpha _{a}]]^{ \mathcal {M},[j],g}=\Phi (@_{j}(\alpha _{a})^{\hat {g}})=\Phi (@_{i}(@_{j}(\alpha _{a})^{\hat {g}}))$
, where
$\lbrack \lbrack @_{s}\alpha _{a}]]^{\mathcal {M},[i],g}=[[\alpha _{a}]]^{ \mathcal {M},[j],g}=\Phi (@_{j}(\alpha _{a})^{\hat {g}})=\Phi (@_{i}(@_{j}(\alpha _{a})^{\hat {g}}))$
, where
 $[j]=g(s)$
, by Induction hypothesis and Corollary 9.14. Finally,
$[j]=g(s)$
, by Induction hypothesis and Corollary 9.14. Finally,
 $\Phi (@_{i}(@_{j}(\alpha _{a})^{\hat {g}}))=\Phi (@_{i}(@_{s}\alpha _{a})^{\hat {g}}))$
by definition of
$\Phi (@_{i}(@_{j}(\alpha _{a})^{\hat {g}}))=\Phi (@_{i}(@_{s}\alpha _{a})^{\hat {g}}))$
by definition of
 $\widehat {g}$
(
$\widehat {g}$
(
 $(@_{s}\alpha _{a})^{\hat {g}}:=@_{j}(\alpha _{a})^{\hat {g}}$
).
$(@_{s}\alpha _{a})^{\hat {g}}:=@_{j}(\alpha _{a})^{\hat {g}}$
). -
(9) Equality expressions: We want to prove that
 $\lbrack \lbrack (\alpha _{a}\equiv \delta _{a})]]^{\mathcal {\ M},[i],g}=\Phi (@_{i}(\alpha _{a}\equiv \delta _{a})^{\widehat {g}})$
. As we said in previous Remark 10.2,
$\lbrack \lbrack (\alpha _{a}\equiv \delta _{a})]]^{\mathcal {\ M},[i],g}=\Phi (@_{i}(\alpha _{a}\equiv \delta _{a})^{\widehat {g}})$
. As we said in previous Remark 10.2,
 $@_{i}(\alpha _{a}\equiv \delta _{a})^{\widehat {g}}=@_{i}((\alpha _{a})^{ \widehat {g}}\equiv (\delta _{a})^{\widehat {g}})$
. By the induction hypothesis we have that
$@_{i}(\alpha _{a}\equiv \delta _{a})^{\widehat {g}}=@_{i}((\alpha _{a})^{ \widehat {g}}\equiv (\delta _{a})^{\widehat {g}})$
. By the induction hypothesis we have that
 $\lbrack \lbrack \alpha _{a}]]^{\mathcal {M},[i],g}=\Phi (@_{i}(\alpha _{a})^{\widehat {g}})\text { and }[[\delta _{a}]]^{\mathcal {M},[i],g}=\Phi (@_{i}(\delta _{a})^{\widehat {g}})$
.
$\lbrack \lbrack \alpha _{a}]]^{\mathcal {M},[i],g}=\Phi (@_{i}(\alpha _{a})^{\widehat {g}})\text { and }[[\delta _{a}]]^{\mathcal {M},[i],g}=\Phi (@_{i}(\delta _{a})^{\widehat {g}})$
.By the definition of
 $\Phi $
and assuming that
$\Phi $
and assuming that
 $\Gamma ^{\ast }\vdash \mathsf {DEN}(@_{i}(\alpha _{a})^{\widehat {g}})$
and
$\Gamma ^{\ast }\vdash \mathsf {DEN}(@_{i}(\alpha _{a})^{\widehat {g}})$
and
 $\Gamma ^{\ast }\vdash \mathsf {DEN}(@_{i}(\delta _{a})^{\widehat {g}})$
, we have:
$\Gamma ^{\ast }\vdash \mathsf {DEN}(@_{i}(\delta _{a})^{\widehat {g}})$
, we have:
 $ [[(\alpha _{a}\equiv \delta _{a})]]^{\mathcal {M},[i],g}=T$
iff
$ [[(\alpha _{a}\equiv \delta _{a})]]^{\mathcal {M},[i],g}=T$
iff
 $[[\alpha _{a}]]^{\mathcal {M},[i],g}=[[\delta _{a}]]^{\mathcal {M} ,[i],g}$
and both are
$[[\alpha _{a}]]^{\mathcal {M},[i],g}=[[\delta _{a}]]^{\mathcal {M} ,[i],g}$
and both are
 $\not =\divideontimes $
iff
$\not =\divideontimes $
iff
 $\Phi (@_{i}(\alpha _{a})^{\widehat {g}})=\Phi (@_{i}(\delta _{a})^{\widehat {g}})$
iff
$\Phi (@_{i}(\alpha _{a})^{\widehat {g}})=\Phi (@_{i}(\delta _{a})^{\widehat {g}})$
iff
 $\Gamma ^{\ast }\vdash @_{i}(\alpha _{a})^{\widehat {g}}\equiv @_{i}(\delta _{a})^{\widehat {g}}$
iff
$\Gamma ^{\ast }\vdash @_{i}(\alpha _{a})^{\widehat {g}}\equiv @_{i}(\delta _{a})^{\widehat {g}}$
iff
 $\Gamma ^{\ast }\vdash @_{i}(\alpha _{a}\equiv \delta _{a})^{ \widehat {g}}$
(by Axiom 5a) iff
$\Gamma ^{\ast }\vdash @_{i}(\alpha _{a}\equiv \delta _{a})^{ \widehat {g}}$
(by Axiom 5a) iff
 $\Phi (@_{i}(\alpha _{a}\equiv \delta _{a})^{\widehat {g}})=T$
.
$\Phi (@_{i}(\alpha _{a}\equiv \delta _{a})^{\widehat {g}})=T$
.In case
 $\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(@_{i}(\alpha _{a})^{ \widehat {g}})$
, the values
$\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(@_{i}(\alpha _{a})^{ \widehat {g}})$
, the values
 $\Phi (@_{i}(\alpha _{a})^{\widehat {g} })=\divideontimes =[[\alpha _{a}]]^{\mathcal {M},[i],g}$
are undefined and the formula is false,
$\Phi (@_{i}(\alpha _{a})^{\widehat {g} })=\divideontimes =[[\alpha _{a}]]^{\mathcal {M},[i],g}$
are undefined and the formula is false,
 $[[(\alpha _{a}\equiv \delta _{a})]]^{\mathcal {M} ,[i],g}=F$
. The same happens when
$[[(\alpha _{a}\equiv \delta _{a})]]^{\mathcal {M} ,[i],g}=F$
. The same happens when
 $\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(@_{i}(\delta _{a})^{\widehat {g}})$
.
$\Gamma ^{\ast }\vdash \lnot \mathsf {DEN}(@_{i}(\delta _{a})^{\widehat {g}})$
. -
(10) Diamond formulas: We want to prove that
 $[[\Diamond \varphi ]]^{\mathcal {M},[i],g}=\Phi (@_{i}(\Diamond \varphi )^{\widehat {g}})$
.
$[[\Diamond \varphi ]]^{\mathcal {M},[i],g}=\Phi (@_{i}(\Diamond \varphi )^{\widehat {g}})$
.For the right-to-left direction, let
 $\Phi (@_{i}(\Diamond \varphi )^{ \widehat {g}})=T$
. Then,
$\Phi (@_{i}(\Diamond \varphi )^{ \widehat {g}})=T$
. Then,
 $@_{i}(\Diamond \varphi )^{\widehat {g}}\in \Gamma ^{\ast }$
. By
$@_{i}(\Diamond \varphi )^{\widehat {g}}\in \Gamma ^{\ast }$
. By
 $\Diamond $
-saturation, there is a nominal j such that
$\Diamond $
-saturation, there is a nominal j such that
 $ @_{i}\Diamond j\in \Gamma ^{\ast }$
and
$ @_{i}\Diamond j\in \Gamma ^{\ast }$
and
 $@_{j}(\varphi )^{\widehat {g}}\in \Gamma ^{\ast }$
. Thus
$@_{j}(\varphi )^{\widehat {g}}\in \Gamma ^{\ast }$
. Thus
 $\Phi (@_{j}(\varphi )^{\widehat {g}})=T$
, and by the induction hypothesis,
$\Phi (@_{j}(\varphi )^{\widehat {g}})=T$
, and by the induction hypothesis,
 $[[\varphi ]]^{\mathcal {M},[j],g}=T$
. Thus
$[[\varphi ]]^{\mathcal {M},[j],g}=T$
. Thus
 $[[\Diamond \varphi ]]^{\mathcal {M},[i],g}=T$
, as
$[[\Diamond \varphi ]]^{\mathcal {M},[i],g}=T$
, as
 $@_{i}\Diamond j\in \Gamma ^{\ast }$
ensures that
$@_{i}\Diamond j\in \Gamma ^{\ast }$
ensures that
 $\left \langle [i],[j]\right \rangle \in R$
.
$\left \langle [i],[j]\right \rangle \in R$
.For the left-to-right direction, let
 $[[\Diamond \varphi ]]^{\mathcal {M },[i],g}=T$
. Thus there is a world
$[[\Diamond \varphi ]]^{\mathcal {M },[i],g}=T$
. Thus there is a world
 $[j]$
such that
$[j]$
such that
 $\left \langle [i],[j]\right \rangle \in R$
and
$\left \langle [i],[j]\right \rangle \in R$
and
 $[[\varphi ]]^{\mathcal {M},[j],g}=T$
. So
$[[\varphi ]]^{\mathcal {M},[j],g}=T$
. So
 $ @_{i}\Diamond j\in \Gamma ^{\ast }$
and
$ @_{i}\Diamond j\in \Gamma ^{\ast }$
and
 $@_{j}(\varphi )^{\widehat {g}}\in \Gamma ^{\ast }$
(by the induction hypothesis and the definition of R). By Theorem Bridge
$@_{j}(\varphi )^{\widehat {g}}\in \Gamma ^{\ast }$
(by the induction hypothesis and the definition of R). By Theorem Bridge
 $_{\Diamond }$
(on page 14)
$_{\Diamond }$
(on page 14)
 $@_{i}\Diamond (\varphi )^{\widehat {g}}\in \Gamma ^{\ast }$
and so
$@_{i}\Diamond (\varphi )^{\widehat {g}}\in \Gamma ^{\ast }$
and so
 $\Phi (@_{i}(\Diamond \varphi )^{\widehat {g}})=T$
.
$\Phi (@_{i}(\Diamond \varphi )^{\widehat {g}})=T$
. -
(11) Universal modality formulas:
 $\mathsf {E}\varphi \in \mathsf {ME}_{t}$
. The right-to-left direction is like the
$\mathsf {E}\varphi \in \mathsf {ME}_{t}$
. The right-to-left direction is like the
 $\Diamond $
-formulas case, but using
$\Diamond $
-formulas case, but using
 $\mathsf {E}$
-saturation instead of
$\mathsf {E}$
-saturation instead of
 $\Diamond $
-saturation. The left-to-right direction is also like the
$\Diamond $
-saturation. The left-to-right direction is also like the
 $\Diamond $
-formulas case, but using Bridge
$\Diamond $
-formulas case, but using Bridge
 $_{\mathsf {E}}$
instead of Bridge
$_{\mathsf {E}}$
instead of Bridge
 $_{\Diamond }$
. We use as well Axioms 6a and 6b.
$_{\Diamond }$
. We use as well Axioms 6a and 6b. -
(12) Downarrow formulas: We will prove that
 $[[{{\downarrow \hspace {-0.1 pt}} }s\varphi ]]^{\mathcal {M} ,[i],g}=\Phi (@_{i}(\,{{\downarrow \hspace {-0.1 pt}} }s\varphi )^{\widehat {g}})$
. This follows straightforwardly:
$[[{{\downarrow \hspace {-0.1 pt}} }s\varphi ]]^{\mathcal {M} ,[i],g}=\Phi (@_{i}(\,{{\downarrow \hspace {-0.1 pt}} }s\varphi )^{\widehat {g}})$
. This follows straightforwardly:
 $[[{{\downarrow \hspace {-0.1 pt}} }s\varphi ]]^{\mathcal {M} ,[i],g}=T$
iff
$[[{{\downarrow \hspace {-0.1 pt}} }s\varphi ]]^{\mathcal {M} ,[i],g}=T$
iff
 $[[\varphi ]]^{\mathcal {M},[i],g_{s}^{[i]}}=T$
iff
$[[\varphi ]]^{\mathcal {M},[i],g_{s}^{[i]}}=T$
iff
 $[[\varphi \frac {i}{s}]]^{\mathcal {M},[i],g}=T$
(using Lemma 4.6 on state variable substitution) iff
$[[\varphi \frac {i}{s}]]^{\mathcal {M},[i],g}=T$
(using Lemma 4.6 on state variable substitution) iff
 $\Phi (@_{i}(\varphi \frac {i}{s})^{\widehat {g}})=T$
(by induction hypothesis on
$\Phi (@_{i}(\varphi \frac {i}{s})^{\widehat {g}})=T$
(by induction hypothesis on
 $ \varphi \frac {i}{s}$
, and also note that
$ \varphi \frac {i}{s}$
, and also note that
 $\widehat {g}$
is the same in
$\widehat {g}$
is the same in
 $(\,{ {\downarrow \hspace {-0.1 pt}} }s\varphi )^{\widehat {g}}$
as in
$(\,{ {\downarrow \hspace {-0.1 pt}} }s\varphi )^{\widehat {g}}$
as in
 $(\varphi \frac {i}{s})^{ \widehat {g}}$
because both
$(\varphi \frac {i}{s})^{ \widehat {g}}$
because both
 ${{\downarrow \hspace {-0.1 pt}} }s\varphi $
and
${{\downarrow \hspace {-0.1 pt}} }s\varphi $
and
 $\varphi \frac {i}{s }$
have the same free variables) iff
$\varphi \frac {i}{s }$
have the same free variables) iff
 $@_{i}(\varphi \frac {i}{s})^{\widehat {g} }\in \Gamma ^{\ast }$
iff
$@_{i}(\varphi \frac {i}{s})^{\widehat {g} }\in \Gamma ^{\ast }$
iff
 $@_{i}(\varphi ^{\widehat {g}}\frac {i}{s})\in \Gamma ^{\ast }$
iff
$@_{i}(\varphi ^{\widehat {g}}\frac {i}{s})\in \Gamma ^{\ast }$
iff
 $@_{i}({{\downarrow \hspace {-0.1 pt}} }s(\varphi )^{\widehat {g}})\in \Gamma ^{\ast }$
(by the DA schema (Axiom 7), and Axiom 5a) iff
$@_{i}({{\downarrow \hspace {-0.1 pt}} }s(\varphi )^{\widehat {g}})\in \Gamma ^{\ast }$
(by the DA schema (Axiom 7), and Axiom 5a) iff
 $@_{i}({{\downarrow \hspace {-0.1 pt}} }s\varphi )^{\widehat {g}}\in \Gamma ^{\ast }$
iff
$@_{i}({{\downarrow \hspace {-0.1 pt}} }s\varphi )^{\widehat {g}}\in \Gamma ^{\ast }$
iff
 $\Phi (@_{i}({{\downarrow \hspace {-0.1 pt}} }s\varphi )^{\widehat {g}})=T$
.
$\Phi (@_{i}({{\downarrow \hspace {-0.1 pt}} }s\varphi )^{\widehat {g}})=T$
.
Acknowledgements
The authors are extremely grateful to the anonymous referee for perceptive questions and detailed comments on the previous version of this article.
Funding
This research was funded by the Spanish Ministerio de Economía y Competitividad project Intensionality as a unifier: Logic, Language and Philosophy, FFI2017-82554, hosted by the Universidad de Salamanca. M. Martins was also supported by Portuguese funding agency FCT, within the project UIDB/04106/2020 at CIDMA.