We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
$L$-functions
In this paper we prove some one-level density results for the low-lying zeros of families of quadratic and quartic Hecke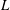 
$L$-functions of the Gaussian field. As corollaries, we deduce that at least 94.27% and 5%, respectively, of the members of the quadratic family and the quartic family do not vanish at the central point.
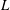$L$-Fu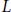nctions and the Distribution of Totally Positive Integers
Let 
$K$ be a totally real number field of degree 
$n$. We show that the number of totally positive integers (or more generally the number of totally positive elements of a given fractional ideal) of given trace is evenly distributed around its expected value, which is obtained from geometric considerations. This result depends on unfolding an integral over a compact torus.
