We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We determine a bound for the valency in a family of dihedrants of twice odd prime orders which guarantees that the Cayley graphs are Ramanujan graphs. We take two families of Cayley graphs with the underlying dihedral group of order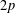 
$2p$ : one is the family of all Cayley graphs and the other is the family of normal ones. In the normal case, which is easier, we discuss the problem for a wider class of groups, the Frobenius groups. The result for the family of all Cayley graphs is similar to that for circulants: the prime 
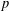$p$ is ‘exceptional’ if and only if it is represented by one of six specific quadratic polynomials.
