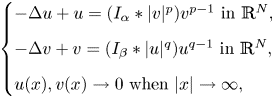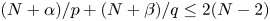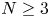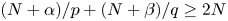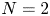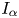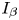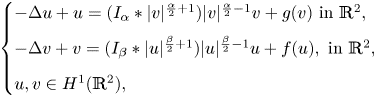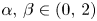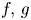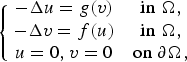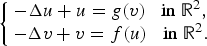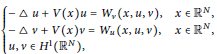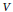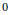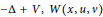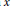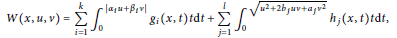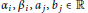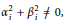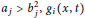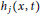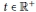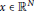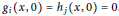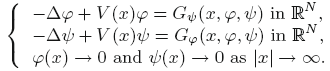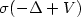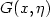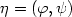In this paper, we investigate the existence and nonexistence of results for a class of Hamiltonian-Choquard-type elliptic systems. We show the nonexistence of classical nontrivial solutions for the problem

\[ \begin{cases} -\Delta u + u= ( I_{\alpha} \ast |v|^{p} )v^{p-1} \text{ in } \mathbb{R}^{N},\\ -\Delta v + v= ( I_{\beta} \ast |u|^{q} )u^{q-1} \text{ in } \mathbb{R}^{N}, \\ u(x),v(x) \rightarrow 0 \text{ when } |x|\rightarrow \infty, \end{cases} \]

$(N+\alpha )/p + (N+\beta )/q \leq 2(N-2)$

$N\geq 3$

$(N+\alpha )/p + (N+\beta )/q \geq 2N$

$N=2$

$I_{\alpha }$

$I_{\beta }$

\[ \begin{cases} -\Delta u + u= (I_{\alpha} \ast |v|^{\frac{\alpha}{2}+1})|v|^{\frac{\alpha}{2}-1}v + g(v) \hbox{ in } \mathbb{R}^{2},\\ - \Delta v + v= (I_{\beta} \ast |u|^{\frac{\beta}{2}+1})|u|^{\frac{\beta}{2}-1}u + f(u), \hbox{ in } \mathbb{R}^{2},\\ u,v \in H^{1}(\mathbb{R}^{2}), \end{cases} \]

$\alpha ,\,\beta \in (0,\,2)$

$f,\,g$

The aim of this paper is to study Hamiltonian elliptic system of the form 0.1

$$\left\{ {\matrix{ {-\Delta u = g(v)} & {{\rm in}\;\Omega,} \cr {-\Delta v = f(u)} & {{\rm in}\;\Omega,} \cr {u = 0,v = 0} & {{\rm on}\;\partial \Omega,} \cr } } \right.$$

0.2

$$\left\{ {\matrix{ {-\Delta u + u = g(v)\;\;\;{\rm in}\;{\open R}^2,} \cr {-\Delta v + v = f(u)\;\;\;{\rm in}\;{\open R}^2.} \cr } } \right.$$

This paper is concerned with the following elliptic system of Hamiltonian type

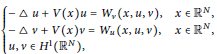$$\left\{ \begin{align} & -\Delta u+V\left( x \right)u={{W}_{v}}\left( x,u,v \right),\,x\in {{\mathbb{R}}^{N}}, \\ & -\Delta v+V\left( x \right)v={{W}_{u}}\left( x,u,v \right),\,x\in {{\mathbb{R}}^{N}}, \\ & u,v\in {{H}^{1}}\left( {{\mathbb{R}}^{N}} \right), \\ \end{align} \right.$$

where the potential 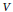$V$ is periodic and 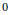$0$ lies in a gap of the spectrum of 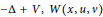$-\Delta +V,W\left( x,u,v \right)$ is periodic in 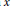$x$ and superlinear in $u$ and $v$ at infinity. We develop a direct approach to finding ground state solutions of Nehari–Pankov type for the above system. Our method is especially applicable to the case when

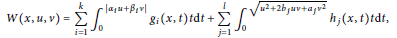$$W\left( x,u,v \right)=\sum\limits_{i=1}^{k}{\,\int _{0}^{\left| \alpha iu+\beta iv \right|}\,{{g}_{i}}\left( x,\,t \right)t\text{d}t+\sum\limits_{j=1}^{l}{\int_{0}^{\sqrt{{{u}^{2}}+2{{b}_{juv+aj{{v}^{2}}}}}}{{{h}_{j}}\left( x,t \right)tdt,}}}$$

where 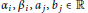${{\alpha }_{i}},{{\beta }_{i}},{{a}_{j}},{{b}_{j}}\in \mathbb{R}$ with 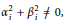$\alpha _{i}^{2}+\beta _{i}^{2}\ne 0$, and 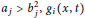${{a}_{j}}>b_{j}^{2},{{g}_{i}}\left( x,t \right)$ and 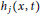${{h}_{j}}\left( x,t \right)$ are nondecreasing in 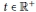$t\in {{\mathbb{R}}^{+}}$ for every 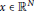$x\in {{\mathbb{R}}^{N}}$ and 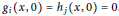${{g}_{i}}\left( x,0 \right)={{h}_{j}}\left( x,0 \right)=0$.

This paper is concerned with the following periodic Hamiltonianelliptic system

$ \{ -\Delta \varphi+V(x)\varphi=G_\psi(x,\varphi,\psi)\ \hbox{in }\mathbb{R}^N, \\-\Delta \psi+V(x)\psi=G_\varphi(x,\varphi,\psi)\ \hbox{in }\mathbb{R}^N, \\\varphi(x)\to 0\ \hbox{and }\psi(x)\to0\ \hbox{as }|x|\to\infty.$

Assuming the potential V is periodic and 0 lies in a gap of $\sigma(-\Delta+V)$ , $G(x,\eta)$ is periodic in x andasymptotically quadratic in $\eta=(\varphi,\psi)$ , existence andmultiplicity of solutions areobtained via variational approach.