Search

We answer some questions in a paper by Kaneko and Koike [‘On modular forms arising from a differential equation of hypergeometric type’, Ramanujan J. 7(1–3) (2003), 145–164] about the modularity of the solutions of a certain differential equation. In particular, we provide a number-theoretic explanation of why the modularity of the solutions occurs in some cases and does not occur in others. This also proves their conjecture on the completeness of the list of modular solutions after adding some missing cases.

We determine the index of five of the seven hypergeometric Calabi–Yau operators that have finite index in $\mathit{Sp}_{4}(\mathbb{Z})$ and in two cases give a complete description of the monodromy group. Furthermore, we find six nonhypergeometric Calabi–Yau operators with finite index in $\mathit{Sp}_{4}(\mathbb{Z})$, most notably a case where the index is one.

Search Results

Refine search

Refine search

Actions for selected content:

2 results

ON THE MODULARITY OF SOLUTIONS TO CERTAIN DIFFERENTIAL EQUATIONS OF HYPERGEOMETRIC TYPE

SOME MONODROMY GROUPS OF FINITE INDEX IN $\mathit{Sp}_{4}(\mathbb{Z})$

Search Results

Refine search

Refine search

Actions for selected content:

Save Search

2 results

ON THE MODULARITY OF SOLUTIONS TO CERTAIN DIFFERENTIAL EQUATIONS OF HYPERGEOMETRIC TYPE

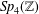SOME MONODROMY GROUPS OF FINITE INDEX IN $\mathit{Sp}_{4}(\mathbb{Z})$