We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Suppose that 
$G$ is an abelian group,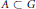 
$A\,\subset \,G$ is finite with 
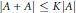$\left| A\,+\,A \right|\,\le \,K\left| A \right|$ and 
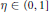$\eta \,\in \,(0,\,1]$ is a parameter. Our main result is that there is a set 
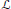$L$ such that
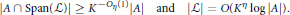$$\left| A\,\cap \,\text{Span}\left( L \right) \right|\ge {{K}^{-{{O}_{n}}\left( 1 \right)}}\left| A \right|\,\,\,\,\text{and}\,\,\,\,\,\left| L \right|=O\left( {{K}^{n}}\log \left| A \right| \right).$$
We include an application of this result to a generalisation of the Roth-Meshulam theorem due to Liu and Spencer
