This paper studies ‘pro-excision’ for the 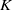 $K$-theory of one-dimensional, usually semi-local, rings and its
various applications. In particular, we prove Geller’s conjecture for equal
characteristic rings over a perfect field of finite characteristic, give results
towards Geller’s conjecture in mixed characteristic, and we establish various
finiteness results for the
$K$-theory of one-dimensional, usually semi-local, rings and its
various applications. In particular, we prove Geller’s conjecture for equal
characteristic rings over a perfect field of finite characteristic, give results
towards Geller’s conjecture in mixed characteristic, and we establish various
finiteness results for the 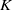 $K$-groups of singularities, covering both orders in number fields and
singular curves over finite fields.
$K$-groups of singularities, covering both orders in number fields and
singular curves over finite fields.
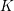 $K$-theory revisited
$K$-theory revisited
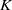 $K$-theory of one-dimensional rings via pro-excision
$K$-theory of one-dimensional rings via pro-excision