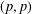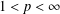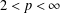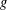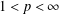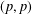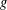A Littlewood–Paley operator associated with the reflection part of the Dunkl operator is introduced and proved to be of type $(p,p)$ for $1<p<\infty$, based on boundedness of a generalised vector-valued singular integral. This fills a gap for $2<p<\infty$ concerning the boundedness of a $g$-function in the Dunkl setting. The paper also supplies new proofs for $1<p<\infty$ on the $(p,p)$ boundedness of various $g$-functions associated with the Dunkl operator.

We introduce quasi-invariant polynomials for an arbitrary finite complex reflection group W. Unlike in the Coxeter case, the space of quasi-invariants of a given multiplicity is not, in general, an algebra but a module Qk over the coordinate ring of a (singular) affine variety Xk. We extend the main results of Berest et al. [Cherednik algebras and differential operators on quasi-invariants, Duke Math. J. 118 (2003), 279–337] to this setting: in particular, we show that the variety Xk and the module Qk are Cohen–Macaulay, and the rings of differential operators on Xk and Qk are simple rings, Morita equivalent to the Weyl algebra An(ℂ) , where n=dim Xk. Our approach relies on representation theory of complex Cherednik algebras introduced by Dunkl and Opdam [Dunkl operators for complex reflection groups, Proc. London Math. Soc. (3) 86 (2003), 70–108] and is parallel to that of Berest et al. As an application, we prove the existence of shift operators for an arbitrary complex reflection group, confirming a conjecture of Dunkl and Opdam. Another result is a proof of a conjecture of Opdam, concerning certain operations (KZ twists) on the set of irreducible representations of W.

Dunkl operators for complex reflection groups are defined in this paper. These commuting operators give rise to a parameterized family of deformations of the polynomial De Rham complex. This leads to the study of the polynomial ring as a module over the ‘rational Cherednik algebra’, and a natural contravariant form on this module. In the case of the imprimitive complex reflection groups $G(m, p, N)$, the set of singular parameters in the parameterized family of these structures is described explicitly, using the theory of non-symmetric Jack polynomials.

2000 Mathematical Subject Classification: 20F55 (primary), 52C35, 05E05, 33C08 (secondary).