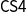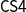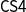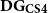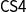The proof theory of the constructive modal logic S4 (hereafter
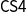 $\mathsf{CS4}$
) has been settled since the beginning of this century by means of either standard natural deduction and sequent calculi or by the reconstruction of modal logic through hypothetical and categorical judgments à la Martin-Löf, an approach carried out by using a special kind of sequents, which keeps two separated contexts representing ordinary and enhanced hypotheses, intuitively interpreted as true and valid assumptions. These so-called dual-context sequents, originated in linear logic, are used to define a natural deduction system handling judgments of validity, truth, and possibility, resulting in a formalism equivalent to an axiomatic system for
$\mathsf{CS4}$
) has been settled since the beginning of this century by means of either standard natural deduction and sequent calculi or by the reconstruction of modal logic through hypothetical and categorical judgments à la Martin-Löf, an approach carried out by using a special kind of sequents, which keeps two separated contexts representing ordinary and enhanced hypotheses, intuitively interpreted as true and valid assumptions. These so-called dual-context sequents, originated in linear logic, are used to define a natural deduction system handling judgments of validity, truth, and possibility, resulting in a formalism equivalent to an axiomatic system for
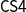 $\mathsf{CS4}$
. However, this proof-theoretical study of
$\mathsf{CS4}$
. However, this proof-theoretical study of
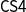 $\mathsf{CS4}$
lacks, to the best of our knowledge, its third fundamental constituent, namely a sequent calculus. In this paper, we define such a dual-context formalism, called
$\mathsf{CS4}$
lacks, to the best of our knowledge, its third fundamental constituent, namely a sequent calculus. In this paper, we define such a dual-context formalism, called
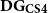 ${\bf DG_{CS4}}$
, and provide detailed proofs of the admissibility for the ordinary cut rule as well as the elimination of a second cut rule, which manipulates enhanced hypotheses. Furthermore, we make available a formal verification of the equivalence of this proposal with the previously defined axiomatic and dual-context natural deduction systems for
${\bf DG_{CS4}}$
, and provide detailed proofs of the admissibility for the ordinary cut rule as well as the elimination of a second cut rule, which manipulates enhanced hypotheses. Furthermore, we make available a formal verification of the equivalence of this proposal with the previously defined axiomatic and dual-context natural deduction systems for
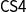 $\mathsf{CS4}$
, using the Coq proof-assistant.
$\mathsf{CS4}$
, using the Coq proof-assistant.