1 results
Resonance of minimizers for n-level quantum systemswith an arbitrary cost
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 10 / Issue 4 / October 2004
- Published online by Cambridge University Press:
- 15 October 2004, pp. 593-614
- Print publication:
- October 2004
-
- Article
- Export citation
-
We consider an optimal control problem describing a laser-inducedpopulation transfer on a n-level quantum system. For a convex cost depending only on the moduliof controls (i.e. the lasers intensities),we prove that there always exists a minimizer inresonance. This permits to justifysome strategies used in experimental physics. It is also quite importantbecause it permits to reduce remarkablythe complexity of the problem (and extend some of our previous resultsfor n=2 and n=3): instead of looking for minimizers on thesphere $S^{2n-1}\subset\mathbb{C}^n$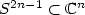
one is reduced to look just forminimizers on the sphere $S^{n-1}\subset \mathbb{R}^n$ 
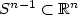. Moreover, for the reduced problem, we investigate on the question of existence of strict abnormal minimizer.
