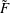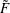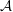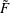Problems with calculations of Berry properties in real and reciprocal spaces and physical characteristics involving manifestations of Berry properties are included.

1. Introduce soliton in quasi-one-dimensional time-dependent Gross-Pitaevskii equation.

2. Introduce the basic idea of topology and the homotopy groups.

3. Introduce vortex in spinless condensate as a typical example of topological defect.

4. Introduce the Berezinskii-Kosterlitz-Thouless transition as a topological defect driven phase transition, and emphasize the topological and energy requirements for such a transition.

5. Discuss the geometric configuration that minimizes the energy of a vortex lattice.

6. Introduce the Majorana stellar representation as a useful tool to visualise the symmetry of a high-spin wave function.

7. Introduce two different phases of spin-1 condensate.

8. Introduce the relation between a mean-field state and the singlet pair condensate.

9. Introduce spin vortex and half vortex in spinor condensate, and discuss various possibilities of spin vortex core.

10. Introduce two categories of topological excitations in a Bose condensate, and introduce monopole and skyrmion as the typical example of each category.

11. Introduce simulating Dirac monopole in synthetic magnetic field.

12. Discuss the symmetry of the Hamiltonian and the symmetry of various phases in a spin-orbit coupled BEC.

13. Discuss the relation between symmetry and phase transitions, using spin-orbit coupled condensate as an example.

14. Discuss the Galilean invariance and the superfluid critical velocity.

Describes Berry’s phase, connection, and curvature, and derives the Chern topological number. It presents two pedagogically important but distinct examples: a two-level system, with its concomitant “magnetic monopole," and the molecular Aharonov–Bohm effect, where the interplay between the quantum electronic andionic motions leads to fascinating topological manifestations.