We consider Markov processes that alternate continuous motions and jumps in a general locally compact Polish space. Starting from a mechanistic construction, a first contribution of this article is to provide conditions on the dynamics so that the associated transition kernel forms a Feller semigroup, and to deduce the corresponding infinitesimal generator. As a second contribution, we investigate the ergodic properties in the special case where the jumps consist of births and deaths, a situation observed in several applications including epidemiology, ecology, and microbiology. Based on a coupling argument, we obtain conditions for convergence to a stationary measure with a geometric rate of convergence. Throughout the article, we illustrate our results using general examples of systems of interacting particles in 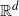 $\mathbb{R}^d$ with births and deaths. We show that in some cases the stationary measure can be made explicit and corresponds to a Gibbs measure on a compact subset of
$\mathbb{R}^d$ with births and deaths. We show that in some cases the stationary measure can be made explicit and corresponds to a Gibbs measure on a compact subset of 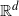 $\mathbb{R}^d$. Our examples include in particular Gibbs measures associated to repulsive Lennard-Jones potentials and to Riesz potentials.
$\mathbb{R}^d$. Our examples include in particular Gibbs measures associated to repulsive Lennard-Jones potentials and to Riesz potentials.