1 results
Smooth and proper maps with respect to a fibration
-
- Journal:
- Mathematical Structures in Computer Science , First View
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
This paper explain how the geometric notions of local contractibility and properness are related to the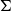
$\Sigma$-types and 
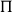$\Pi$-types constructors of dependent type theory. We shall see how every Grothendieck fibration comes canonically with such a pair of notions—called smooth and proper maps—and how this recovers the previous examples and many more. This paper uses category theory to reveal a common structure between geometry and logic, with the hope that the parallel will be beneficial to both fields. The style is mostly expository, and the main results are proved in external references.
