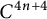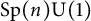We systematically study calibrated geometry in hyperkähler cones $C^{4n+4}$, their 3-Sasakian links $M^{4n+3}$, and the corresponding twistor spaces $Z^{4n+2}$, emphasizing the relationships between submanifold geometries in various spaces. Our analysis highlights the role played by a canonical $\mathrm {Sp}(n)\mathrm {U}(1)$-structure $\gamma $ on the twistor space Z. We observe that $\mathrm {Re}(e^{- i \theta } \gamma )$ is an $S^1$-family of semi-calibrations and make a detailed study of their associated calibrated geometries. As an application, we obtain new characterizations of complex Lagrangian and complex isotropic cones in hyperkähler cones, generalizing a result of Ejiri–Tsukada. We also generalize a theorem of Storm on submanifolds of twistor spaces that are Lagrangian with respect to both the Kähler–Einstein and nearly Kähler structures.

We prove that a reduced and irreducible algebraic surface in $\mathbb{CP}^{3}$ containing infinitely many twistor lines cannot have odd degree. Then, exploiting the theory of quaternionic slice regularity and the normalisation map of a surface, we give constructive existence results for even degrees.

As a generalization of the conformal structure of type (2, 2), we study Grassmannian structures of type (n, m) for n, m ≥ 2. We develop their twistor theory by considering the complete integrability of the associated null distributions. The integrability corresponds to global solutions of the geometric structures.

A Grassmannian structure of type (n, m) on a manifold M is, by definition, an isomorphism from the tangent bundle TM of M to the tensor product V ⊗ W of two vector bundles V and W with rank n and m over M respectively. Because of the tensor product structure, we have two null plane bundles with fibres Pm-1(ℝ) and Pn-1(ℝ) over M. The tautological distribution is defined on each two bundles by a connection. We relate the integrability condition to the half flatness of the Grassmannian structures. Tanaka’s normal Cartan connections are fully used and the Spencer cohomology groups of graded Lie algebras play a fundamental role.

Besides the integrability conditions corrsponding to the twistor theory, the lifting theorems and the reduction theorems are derived. We also study twistor diagrams under Weyl connections.