1 results
On Relaxation Oscillations Governed by a Second Order Differential Equation for a Large Parameter and with a Piecewise Linear Function(1)
-
- Journal:
- Canadian Mathematical Bulletin / Volume 26 / Issue 1 / 01 March 1983
- Published online by Cambridge University Press:
- 20 November 2018, pp. 80-91
- Print publication:
- 01 March 1983
-
- Article
-
- You have access
- Export citation
-
This paper deals with the differential equation: ẍ + μF(ẋ) + x = ƒ( X, ẋ, t/Tμ) for μ ≫ 1 where F is a piecewise linear function and f is a periodic function of period μT, where T is to be chosen. It is established that periodic forced vibrations exist in an annular domain R(μ) constructed for the free vibration (ƒ ≡ 0), provided ƒ is not of higher order than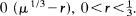
Subsequently with ƒ = A cos (2πt/μT*), an asymptotic treatment of the forced vibration problem is carried out, by finding the proper initial conditions and the proper period μT* of f. Finally it is concluded that μT* is close to the period of the free vibration.
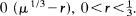Subsequently with 