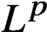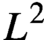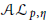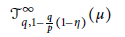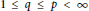2 results
Global boundedness of a class of multilinear Fourier integral operators
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 22 February 2021, e14
-
- Article
-
- You have access
- Open access
- Export citation
-
We establish the global regularity of multilinear Fourier integral operators that are associated to nonlinear wave equations on products of
$L^p$ spaces by proving endpoint boundedness on suitable product spaces containing combinations of the local Hardy space, the local BMO and the
$L^2$ spaces.
The Carleson Measure Problem Between Analytic Morrey Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 4 / 01 December 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 878-890
- Print publication:
- 01 December 2016
-
- Article
-
- You have access
- Export citation
-
The purpose of this paper is to characterize positive measure
$\mu$ on the unit disk such that the analytic Morrey space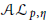 
$\mathcal{A}{{\mathcal{L}}_{p,\eta }}$ is boundedly and compactly embedded to the tent space
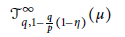$$\mathcal{J}_{q,1-\frac{q}{p}\left( 1-\eta \right)}^{\infty }\left( \mu \right)$$for the case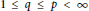
$1\,\le \,q\,\le \,p\,<\,\infty$ respectively. As an application, these results are used to establish the boundedness and compactness of integral operators and multipliers between analytic Morrey spaces.
